Методические РЕКОМЕНДАЦИИ

Кафедра автоматизированных и вычислительных систем

 

 

ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

ЗАДАЧ  НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

 

Методические РЕКОМЕНДАЦИИ

к выполнению курсового проекта

по дисциплине «Аналитические и численные задачи

оптимизации» для бакалавров направления подготовки 09.03.01 «Информатика и вычислительная техника», профиля

«Вычислительные машины, комплексы, системы и сети»

заочной формы обучения

 

 

                  

Воронеж 2019

Составители: канд. техн. наук Т.И.Сергеева,

                  канд. техн. наук М.Ю. Сергеев

 

УДК 681.32

 

Программная реализация задач нелинейного программирования: методические рекомендации к выполнению курсового проекта по дисциплине «Аналитические и численные задачи оптимизации» для студентов направления подготовки 09.03.01 «Информатика и вычислительная техника», профиля «Вычислительные машины, комплексы, системы и сети» заочной формы обучения /ФГБОУ ВО «Воронежский государственный технический университет; сост. Т.И. Сергеева, М.Ю. Сергеев. Воронеж, 2019. 29 с.

 

Методические указания содержат теоретические и практические сведения для поиска экстремума в задачах нелинейного программирования.            

Предназначены для студентов четвертого курса.

 

Табл. 3. Ил. 8. Библиогр.: 5 назв.

 

Рецензент канд. техн. наук, доц. А.М. Нужный

 

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. С.Л. Подвальный

 

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

 

 

© ФГБОУ ВО «Воронежский государственный

                         технический университет», 2019

1. ОБЩИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ

 КУРСОВОГО ПРОЕКТА

 

Курсовой проект по дисциплине «Аналитические и численные задачи оптимизации» позволит получить теоретические сведения и практические навыки решения задач нелинейного программирования, возникающие в различных вычислительных системах.

Цель курсового проекта состоит в вооружении студентов знаниями методов решения нелинейных экстремальных задач без ограничений различного вида и в получении навыков разработки алгоритмов и программ, реализующих решение задач данного класса.

Курсовой проект включает реализацию двух методов решения нелинейных задач без ограничений.

Курсовой проект имеет стандартную структуру и должен состоят из следующих частей:

- введение;

- два раздела, описывающих реализацию методов решения нелинейных задач;

- заключение;

- список литературы.

Общая тема курсового проекта «Программная реализация задач нелинейного программирования».

Выбор варианта курсового проекта осуществляется из таблицы 1.

Выбор конкретного задания для метода «золотого сечения» осуществляют из таблицы 2.

Выбор конкретного задания для метода градиентного спуска с постоянным шагом осуществляют из таблицы 3.

 

Таблица 1

Варианты курсового проекта

 

Порядковый номер студента в списке группы	Номер варианта
	Метод «золотого сечения»	Метод градиентного спуска с постоянным шагом
1	1	12
2	2	11
3	3	10
4	4	9
5	5	8
6	6	7
7	7	6
8	8	5
9	9	4
10	10	3
11	11	2
12	12	1
13	13	12
14	14	11
15	1	10
16	2	9
17	3	8
18	4	7
19	5	6
20	6	5
21	7	4
22	8	3

 

 

Таблица 2

Варианты первого задания

 

Номер варианта	Функция	a	b	E	Ответы X, F
1	F(x) = –e-x·ln(x)	0.1	3	0.001	1.763; -0.097
2	F(x) = –e-x·x	0.1	3	0.001	1.0; -0.368
3	F(x) = 2·x2 + 3·e-x	0	1	0.001	0.469; 2.317
4	F(x) = x2 + x + 5·e-x	0	2	0.001	0.719; 3.672
5	F(x) = 2·x2 – x + e-x	-1	1	0.001	0.415; 0.59
6	F(x) = -3·e-x·ln(2·x)	0.5	2.5	0.001	1.173; -0.792
7	F(x) = x4 – 10·x3+20·x2	4	8	0.001	5.765; -146.726
8	F(x) = x4 – 12·x3+7·x2 – 5·x	8	9.5	0.001	8.61; -1687.886
9	F(x) = x4 –10·x2 + 5·x	-5	5	0.001	-2.352; -36.477
10	F(x) = x4 – 10·x3 + 20·x	6.5	8	0.001	7.409; -905.591
11	F(x) = x4 – 6·x3 – 5·x2 + 10·x	4	6	0.001	4.906; -200.466
12	F(x) = x4 – 10·x3 – 30·x2 – 15·x	8	10	0.001	9.179; -3300.241

Продолжение таблицы 2

Номер варианта	Функция	a	b	E	Ответы X, F
13	F(x) = 2x2 – 12x	0	5	0.01	2.998; -18.00
14	F(x) = 32x2 – 15x + 2	0	0.5	0.01	0.233; 0.242

 

Таблица 3

Варианты второго задания

 

№ вар.	Функция	X	H	Xmin
1	F(x1..x3) = 2*(x1+2)2 + 2*(x2+3)2 + 3*(x3-5)2	( -5, 3, -4)	4	(-2, -3, 5)
2	F(x1..x2) = 2*(x1+7)2 + (x2-11)2	(5, -5)	4	(-7, 11)
3	F(x1..x4) = 2*(x1+1)2 + 4*(x2-2)2 + 6*(x3+3)2 + 8*(x4-4)2	(4,-4,7,-7)	4	(-1,2-3,4)
4	F(x1..x3) =(x1-5)2 + 3*(x2+7)2 + (x3-9)2	(-1,3,7)	4	(5,-7,9)
5	F(x1..x2) =3*(x1+5)2 + 2*(x2-5)2	(4,-4)	4	(-5,5)
6	F(x1..x4) = (x1+7)2 + 2*(x2-7)2 + 3*(x3+7)2 + 4*(x4-7)2	(4,-1,4,-1)	4	(-7,7, -7,7)
7	F(x1..x3) =(x1-25)2 + 2*(x2+27)2 +2*(x3-29)2	(-1, 2, -1)	4	(25, -27, 29)
8	F(x1..x2) =10*(x1+5)2 + 12*(x2-15)2	(10, -10)	4	(-5, 15)

 

 

Продолжение таблицы 3

№ вар.	Функция	X	H	Xmin
9	F(x1..x4) = 4*(x1-5)2 + 3*(x2-10)2 + 2*(x3+15)2 + (x4+20)2	(2, -2, 2, -2)	4	(5, 10, -15, -20)
10	F(x1..x3) = (x1+2)2 + 2*(x2+4)2 + 4*(x3+6)2	(1, 1, 1)	4	(-2, -4, -6)
11	F(x1..x2) =3*(x1-21)2 + 2*(x2+12)2	(-5, -5)	4	(21, -12)
12	F(x1..x4) = 5*(x1+11)2 + 7*(x2+9)2 + 9*(x3+7)2 + 11*(x4+5)2	(2, 2, 2, 2)	4	(-11, -9, -7, -5)

 

2. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА ДЛЯ ФУНКЦИЙ

ОДНОЙ ПЕРЕМЕННОЙ БЕЗ ОГРАНИЧЕНИЙ

 

2.1. Методы одномерной оптимизации

 

Постановка задачи. Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку x^* Î R, что f(x^*) = min f(x), x^*ÎR.

Для методов одномерной минимизации типично задание начального интервала неопределенности L₀ = [a₀,b₀], в котором предположительно находится точка минимума x^*, но ее точное значение неизвестно.

Большинство известных методов одномерной минимизации применяется для класса унимодальной функции.

Определение. Функция f(x) называется унимодальной на интервале L₀ = [a₀,b₀], если она достигает глобального минимума на [a₀,b₀] в единственной точке x^*, причем слева от x^* эта функция строго убывает, а справа от x^* строго возрастает. Если a₀ ≤ y < z < x^*, то f(y) > f(z), а если x^* < y < z ≤ b₀, то f(y) < f(z).

Существуют две различные стратегии выбора точек, в которых производится вычисление значений функции. Если все точки задаются заранее, до начала вычислений, то это пассивная (параллельная) стратегия поиска. Если точки выбираются последовательно в процессе поиска с учетом результатов предыдущих вычислений, то это последовательная стратегия.

Последовательную стратегию можно реализовать следующими способами:

- применением квадратичной и кубической интерполяции, где по нескольким вычисленным значениям функции строится интерполяционный полином, а его минимум указывает на очередное приближение искомой точки экстремума;

- построением последовательности вложенных друг в друга интервалов, каждый из которых содержит точку минимума.

Последовательная стратегия поиска включает в себя три этапа:

- выбор начального интервала неопределенности; границы a₀, b₀ интервала должны быть такими, чтобы функция f(x) была унимодальной;

- уменьшение интервала неопределенности;

- проверка условия окончания поиска; поиск заканчивается, когда длина текущего интервала неопределенности [a_k,b_k] оказывается меньше установленной величины.

Ответом является множество точек, принадлежащих последнему интервалу неопределенности, среди которых каким-либо образом выбирается решение задачи x^*.

Существует достаточно большое количество методов поиска экстремума для функций одной переменной без ограничений. Это следующие методы: метод равномерного поиска, метод деления интервала пополам, метод дихотомии, метод золотого сечения, метод Фибоначчи, метод квадратичной интерполяции.

 

2.2. Метод «золотого сечения»

 

Для построения конкретного метода одномерной оптимизации, работающего по принципу последовательного сокращения интервала неопределенности, следует задать правило выбора на каждом шаге двух внутренних точек. В методе «золотого сечения» в качестве двух внутренних точек выбираются точки золотого сечения.

Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей.

Пусть задана функция f(x) на отрезке [a,b], функция f(x) непрерывна на данном отрезке. Тогда для того, чтобы найти значение этой функции на заданном отрезке, отвечающее критерию поиска минимума, рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях (рис. 1), то есть выбираются две точки x₁ и x₂ такие, что:

где — пропорция золотого сечения.

Рис. 1. Выбор промежуточных точек в методе «золотого     сечения»

Из формул (1) получаем:

                     (2)

Алгоритм решения задачи следующий.

1. Шаг 1. Задают начальные границы отрезка a, b и точность 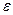, рассчитывают начальные точки деления: ,  и значения в них целевой функции: .

2. Шаг 2.  Если , то

Иначе

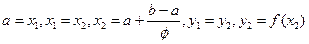
3. Шаг 3.

Если |b - a|< ε, то середина последнего интервала ((x₁ + x₂)/2) является  искомым значением переменной х, обеспечивающим минимум функции, и поиск решения заканчивается. Иначе необходимо осуществить возврат к Шагу 2.

Структурная схема метода представлена на рис. 2.

 

 

Рис. 2. Структурная схема метода «золотого сечения»

 

2.3. Методические рекомендации для написания программы

в среде программирования Delphi (RAD Studio)

 

Возможный вид оконного приложения в среде Delphi представлен на рис. 3. Вид оконного приложения может быть другим.

 

Рис. 3. Возможный вид интерфейса программы

 

Элементы оконного приложения могут быть созданы с использованием следующих компонентов.

Надпись «Нижняя граница» - компонент Label1, свойство Caption.

Надпись «Верхняя граница» - компонент Label2.

Надпись «Точность» - компонент Label3.

Окно для ввода нижней границы – компонент Edit1.

Окно для ввода верхней границы – компонент Edit2.

Окно для ввода точности – компонент Edit3.

Кнопка «Поиск минимума» - компонент Button1, свойство Caption.

Надпись «Промежуточные результаты» - компонент Label4. Надпись Х1 – компонент Label5. Надпись Х2 – компонент Label6.

Окна для вывода промежуточных результатов ListBox1, ListBox2.

Надпись «Результат» - компонент Label7.

Окно для вывода результата (х) – компонент Edit4.

Надпись «Функция» - компонент Label8.

Окно для вывода функции (y) – компонент Edit5.

Кнопка «Выход» - компонент Button2.

Данные, введенные в компоненты Edit, для использования в вычислениях должны быть преобразованы из текстового формата в числовой с использованием следующих функций:

- преобразование строки из Edit1.Text в вещественное число - StrToFloat(Edit1.Text);

- преобразование строки из Edit1.Text в целое число - StrToInt(Edit1.Text).

Преобразование результатов вычислений из числового формата в строковый формат происходит с помощью следующих функций:

- преобразование вещественного числа в текст – функция FloatToStr; например: Edit4.Text := FloatToStr(rez); форматированный вывод: FloatToStrF(rez,ffFixed,8,3);

- преобразование целого числа в текст – функция IntToStr.

Добавление в компонент ListBox промежуточных значений и преобразование вещественного числа в строку осуществляется следующим образом:

ListBox1.Items.Add(FloatToStr(X1));

2.4. Методические рекомендации для написания программы

в среде Visual Studio на языке C#

 

Возможный вид оконного приложения в среде Visual Studio для реализации программы на C# представлен на рис. 4.

Элементы оконного приложения могут быть созданы с использованием следующих компонентов.

Надпись «Введите нижнюю граница» - компонент Label1.

Надпись «Введите верхнюю границу» - компонент Label2.

Надпись «Введите точность» - компонент Label3.

Окно для ввода нижней границы – компонент textBox1.

Окно для ввода верхней границы – компонент textBox2.

Окно для ввода точности – компонент textBox3.

Кнопка «Выход» - компонент Button1.

Кнопка «Поиск экстремума» - компонент Button2.

Надпись Х1 – компонент Label4. Надпись Х2 – компонент Label5.

Окна для вывода промежуточных результатов ListBox1, ListBox2.

Надпись «Результат» - компонент Label6.

Окно для вывода результата (х) – компонент textBox4.

Надпись «Функция» - компонент Label7.

Окно для вывода функции (y) – компонент textBox5.

Для размещения окна формы по центру экрана для свойства формы StartPosition выбирают из списка CenterScreen.

 

 

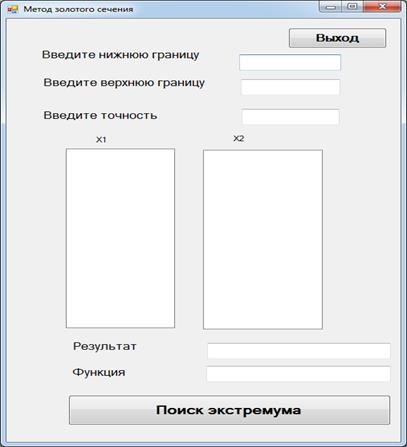
Рис. 4. Оконная форма для ввода данных

 

Элементы программирования на C#

Вещественные переменные описывают с помощью служебного слова double. Например:

double a, b, t, y1, y2;

Ввод данных из поля ввода, например из textBox1 в переменную а, реализуется так:

a = Convert.ToDouble(textBox1.Text);

При этом текстовая переменная преобразуется в вещественное число.

Вычисления с применением математических функций записывают следующим образом:

y1 = -Math.Exp(-x1) * Math.Log(x1);

Оператор цикла с предусловием записывают так:

while (Math.Abs(b - a) >= t)

{

Операторы, повторяющиеся в цикле

}

Вывод переменной (например х1) в компонент listBox1 записывают так:

listBox1.Items.Add(Convert.ToString(x1));

При этом переменная х1 преобразуется в строковый формат представления.

Проверку условия записывают так:

if (y1 <= y2) {операторы, если условие выполняется}

else

{

операторы, если условие не выполняется

}

Вывод результата (функции y) в компонент textBox5 записывают так:

textBox5.Text = Convert.ToString(y);

При этом реализуется преобразование переменной y в строковый формат.

 

 

3. РЕАЛИЗАЦИЯ МЕТОДА ПОИСКА МИНИМУМА

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

С ИСПОЛЬЗОВАНИЕМ МЕТОДА ГРАДИЕНТНОГО

СПУСКА С ПОСТОЯННЫМ ШАГОМ

 

3.1. Теоретические сведения

 

Если в какой-либо точке функция непрерывна и дифференцируема, то в этой точке существует градиент целевой функции. Градиент указывает направление наискорейшего возрастания (подъема) функции, а антиградиент - противоположное направление. Градиент определяется как вектор-столбец частных производных L(x) по x

 

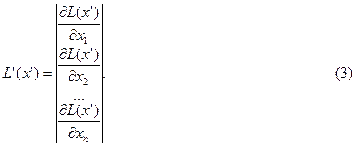
В специальной литературе доказывается, что градиент ортогонален линии уровня (множество точек, для которой целевая функция имеет постоянное значение), проходящей через точку дифференцирования, и направлен в сторону максимума функции (направление наискорейшего подъема). Противоположное направление градиента (антиградиент) указывает направление минимума (направление наискорейшего спуска).

Постановка задачи. Пусть дана функция f(x), ограниченная снизу на множестве Rⁿ и имеющая непрерывные частные производные во всех его точках.

Требуется найти локальный минимум функции f(x) на множестве допустимых решений X = Rⁿ, т.е. найти такую точку х^* ? Rⁿ, что

f(x^*) = min f(x).

x ? Rⁿ

Стратегия поиска. Стратегия решения задачи состоит в построении последовательности точек {x^k}, k = 0,1,… , таких, что f(x^k+1) < f(x^k), k = 0, 1, … . Точки последовательности {x^k} вычисляются по правилу

 

x^k+1 = x^k – t_k Ñf(x^k), k = 0,1,…,                             (4)

 

где точка х⁰ задается пользователем; Ñf(x^k) – градиент функции f(x), вычисленный в точке x^k; величина шага t_k задается пользователем и остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется путем проверки выполнения условия f(x^k+1) - f(x^k) < 0  или f(x^k+1) - f(x^k) <  - ε ǁÑf(x^k)ǁ², 0 < ε < 1.

Построение последовательности {x^k} заканчивается:

- в точке x^k, для которой ‖Ñf(x^k)‖ < ε₁, где ε₁ - заданное малое положительное число (модуль вектора х вычисляется по формуле ‖х‖= ),

- или при k ≥ M, где М – предельное число итераций,

- или при двукратном одновременном выполнении двух неравенств ‖x^k+1 - x^k‖ < ε₂, |f(x^k+1) – f(x^k)| < ε₂, где ε₂ – малое положительное число.

Вопрос о том, может ли точка х^k рассматриваться как найденное приближение искомой точки минимума, требует проведения дополнительных исследований.

Алгоритм. Алгоритм решения задачи состоит из последовательности шагов.

Шаг 1. Задать х⁰, 0 < ε < 1, ε₁ > 0, ε₂ > 0. Например: ε=0.2, ε₁=0.1, ε₂=0.15. Задать М – предельное число итераций (например, М=10). Найти градиент функции в произвольной точке

 

Ñf(x^k) = .

Шаг 2. Положить k=0.

Шаг 3. Вычислить Ñf(x^k).

Шаг 4. Проверить выполнение критерия окончания ‖Ñf(x^k)‖ < ε₁:

- если критерий выполнен, то поиск закончен, х^* = х^k;

- если критерий не выполнен, то перейти к шагу 5.

Шаг 5. Проверить выполнение неравенства k ≥ M:

- если неравенство выполнено, то расчет окончен и х^* = х^k;

- если нет, то перейти к шагу 6.

Шаг 6. Задать величину шага t_k. Например: t_k=0.5.

Шаг 7. Вычислить x^k+1 = x^k – t_k Ñf(x^k).

Шаг 8. Проверить выполнение условия

f(x^k+1) - f(x^k) < 0  (или f(x^k+1) - f(x^k) <  - ε ǁÑf(x^k)ǁ²):

- если условие выполнено, то перейти к шагу 9:

- если условие не выполнено, положить t_k = t_k / 2 и перейти к шагу 7.

Шаг 9. Проверить выполнение условий

‖x^k+1 - x^k‖ < ε₂, |f(x^k+1) – f(x^k)| < ε₂:

- если оба условия выполнены при текущем значении k и при предыдущем значении k (k=k-1), то расчет окончен и х^* = х^k+1;

- если хотя бы одно из условий не выполнено, то положить k = k + 1 и перейти к шагу 3.

Геометрическая интерпретация метода для n=2 приведена на рис. 5.

Рис. 5. Геометрическая интерпретация метода  

 

3.2. Структурная схема алгоритма

 

Структурная схема данного метода представлена на рис. 6.

Основные обозначения на схеме следующие:

- х – исходный вещественный массив;

- х1 – промежуточный вещественный массив х;

- xr – массив- решение (вещественный массив);

- rx – разность массивов х1 и х (вещественный массив);

- g- массив-градиент (вещественный массив);

- k – номер (количество) итерации (переменная целого типа);

- m – максимальное количество итераций (переменная целого типа);

- i- параметр цикла (переменная целого типа);

- t – шаг (вещественная переменная);

- е1, е2 – точности (вещественная переменная);

- mm, mm1 – модуль (нормаль) вектора-градиента и разности массивов х1 и х (вещественные переменные);

- u1, u2 – значения функции для массивов х1 и х (вещественные переменные);

- u – разность u1 и u2 (вещественная переменная);

- flag, flag1 -  логические переменные, используемые для организации итерационного цикла.  

 

Если функция цели имеет вид

F(x1, х2, x3) = 2*(x₁+2)² + 2*(x₂+3)² + 3*(x₃-5)²,

то градиент (вектор частных производных) для неё вычисляют следующим образом:

- для х1 частная производная равна 2*2*(х1+2) = 4х1+8;

- для х2 частная производная равна 2*2*(х2+3) = 4х2+12;

- для х3 частная производная равна 2*3*(х3-5) = 6х3-30.

Таким образом, имеем следующий вектор градиента:

g[1] = 4*x[1]+8;

g[2] = 4*x[2]+12;

g[3] = 6*x[3]-30;

 

Модуль градиента вычисляют по формуле:

 mm = sqrt(g[1]*g[1]+g[2]*g[2]+g[3]*g[3]);

                                                                                                             

 

 

 

 

Рис. 6. Структурная схема градиентного метода (начало)

 

 

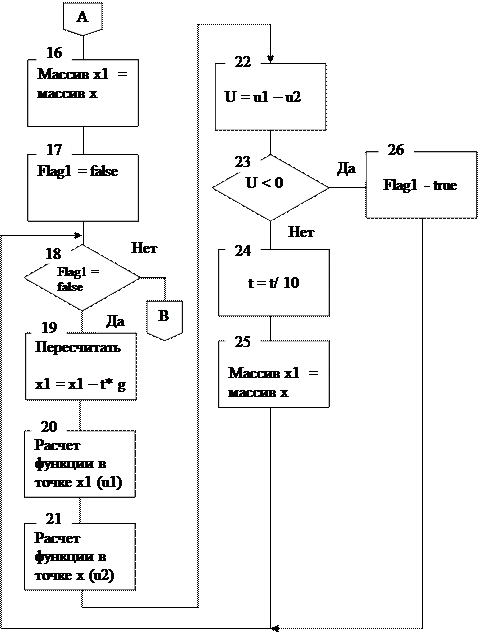
Рис. 6. Структурная схема градиентного метода (продолжение)

 

Рис. 6. Структурная схема градиентного метода (окончание)

 

 

3.3. Методические рекомендации для написания программы

в среде программирования Delphi (RAD Studio)

 

Возможный вид оконного приложения в среде Delphi представлен на рис. 7. Вид оконного приложения может быть другим.

 

Рис. 7. Возможный вид интерфейса для метода

градиентного спуска

 

Элементы оконного приложения могут быть созданы с использованием следующих компонентов.

Надписи «Х1», «Х2», «Х3», «Шаг», «Результаты вычислений» - компоненты Label1, Label2, Label3, Label4, Label5, свойство Caption.

Окна для ввода Х1, Х2, Х3 и шага – компоненты Edit1, Edit2, Edit3, Edit4.

Окно для вывода промежуточных и итоговых результатов ListBox1.

Кнопка «Минимизировать» - компонент Button1, свойство Caption.

Кнопка «Выход» - компонент Button2, свойство Caption.

 

3.4. Методические рекомендации для написания программы

в среде программирования Visual Studio (C#)

 

Возможный вид пользовательского интерфейса представлен на рис. 8.

Элементы оконного приложения могут быть созданы с использованием следующих компонентов.

- надписи с применением компонента label;

- поля для ввода с применением компонента textbox;

- поля для вывода результата с применением компонента listBox;

- кнопки для вызова процедур обработки событий с применением компонента button.

Для размещения окна формы по центру экрана для свойства формы StartPosition выбирают из списка CenterScreen.

 

 

Рис. 8. Вид окна пользовательского интерфейса

 

Элементы программирования на C#

Переменные, используемые в программе, описывают до их использования. Например, описание переменных программы приведено ниже:

       const int n = 3;

       double[] g = new double[n];

       double[] x = new double[n];

       double[] x1 = new double[n];

       double[] xr = new double[n], rx = new double[n];

       int i, m, k;

       double t, e1, e2, mm, mm1, u, u1, u2,ff;

       Boolean flag, flag1;

Во фрагменте описаны целые переменные, массивы, вещественные и логические переменные.

Операторы присваивания приведены ниже:

       e1 = 0.001;

       e2 = 0.015;

       m = 40;

       flag = false;

       k = 0;

Ввод переменных из полей ввода и присвоение их переменным программы:

x[0] = Convert.ToDouble(textBox1.Text);

 x[1] = Convert.ToDouble(textBox2.Text);

 x[2] = Convert.ToDouble(textBox3.Text);

t = Convert.ToDouble(textBox4.Text);