 |
Главная |
Вычисление кратных интегралов
|
из
5.00
|
Обычно при вычислении кратных интегралов методом Монте-Карло используют один из двух способов.
Первый способ.
Пусть требуется вычислить  кратный интеграл
кратный интеграл
 (3.1)
(3.1)
по области G, лежащей в  мерном единичном кубе
мерном единичном кубе

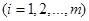
Выберем  равномерно распределённых на отрезке
равномерно распределённых на отрезке 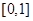 последовательностей случайных чисел
последовательностей случайных чисел

Тогда точки  можно рассматривать как случайные, равномерно распределённые в
можно рассматривать как случайные, равномерно распределённые в  мерном единичном кубе.
мерном единичном кубе.
Пусть из общего числа  случайных точек
случайных точек 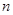 точек попали в область G, остальные
точек попали в область G, остальные  оказались вне G. Тогда при достаточно большом
оказались вне G. Тогда при достаточно большом  имеет место приближенная формула:
имеет место приближенная формула:
 (3.2)
(3.2)
где под  понимается
понимается  мерный объём области интегрирования. Если вычисление объёма
мерный объём области интегрирования. Если вычисление объёма  затруднительно, то можно принять
затруднительно, то можно принять  , и для приближенного вычисления интеграла получим:
, и для приближенного вычисления интеграла получим:
 (3.3)
(3.3)
Указанный способ можно применить к вычислению кратных интегралов и для произвольной области  , если существует такая замена переменных, при которой новая область интегрирования будет заключена в
, если существует такая замена переменных, при которой новая область интегрирования будет заключена в  мерном единичном кубе.
мерном единичном кубе.
Второй способ.
Если функция  , то интеграл (3.1) можно рассматривать как объём тела в
, то интеграл (3.1) можно рассматривать как объём тела в  мерном пространстве, т.е.
мерном пространстве, т.е.
 (3.5)
(3.5)
где область интегрирования  определяется условиями
определяется условиями 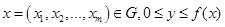
Если в области 
 , то введя новую переменную
, то введя новую переменную  , получим
, получим

где область  лежит в единичном
лежит в единичном 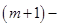 мерном кубе
мерном кубе 
Возьмём  равномерно распределенных на отрезке
равномерно распределенных на отрезке  случайных последовательностей
случайных последовательностей
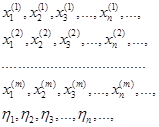
Составим соответствующую последовательность случайных точек 
Пусть из общего числа  случайных точек
случайных точек  точек принадлежат объёму
точек принадлежат объёму  , тогда имеет место приближенная формула
, тогда имеет место приближенная формула
 (3.6)
(3.6)
Практическая часть
Пример 1
Вычислим приближенно интеграл 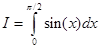
Точное значение его известно: 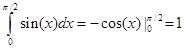
Используем для вычисления две различные случайные величины  , с постоянной плотностью
, с постоянной плотностью  (т.е.
(т.е.  равномерна распределена в интервале
равномерна распределена в интервале 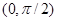 ) и с линейной плотностью
) и с линейной плотностью  .Линейная плотность более соответствует рекомендации о пропорциональности
.Линейная плотность более соответствует рекомендации о пропорциональности  и
и  . Поэтому следует ожидать, что второй способ вычисления даст лучший результат.
. Поэтому следует ожидать, что второй способ вычисления даст лучший результат.
1) Пусть  , формула для разыгрывания
, формула для разыгрывания  имеет вид
имеет вид  . А формула (2.2) примет вид
. А формула (2.2) примет вид  .
.
Пусть  . В качестве значений
. В качестве значений 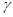 используем тройки чисел из табл. 1 (см. приложение), умноженные на 0.001. Промежуточные результаты сведены в табл. 2.1. Результат расчёта
используем тройки чисел из табл. 1 (см. приложение), умноженные на 0.001. Промежуточные результаты сведены в табл. 2.1. Результат расчёта 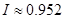
Таблица 2.1

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

| 0.865 | 0.159 | 0.079 | 0.566 | 0.155 | 0.664 | 0.345 | 0.655 | 0.812 | 0.332 |
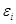
| 1.359 | 0.250 | 0.124 | 0.889 | 0.243 | 1.043 | 0.542 | 1.029 | 1.275 | 0.521 |

| 0.978 | 0.247 | 0.124 | 0.776 | 0.241 | 0.864 | 0.516 | 0.857 | 0.957 | 0.498 |
2) пусть теперь  . Для разыгрывания
. Для разыгрывания 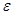 используем формулу
используем формулу
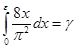 ,
,
откуда получаем

формула (2.2) имеет вид

Пусть  . Числа выберем те же, что и в случае 1. Промежуточные результаты сведены в табл. 2.2. Результат расчёта
. Числа выберем те же, что и в случае 1. Промежуточные результаты сведены в табл. 2.2. Результат расчёта 
Таблица 2.2

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

| 0.865 | 0.159 | 0.079 | 0.566 | 0.155 | 0.664 | 0.345 | 0.655 | 0.812 | 0.332 |
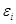
| 1.461 | 0.626 | 0.442 | 1.182 | 0.618 | 1.280 | 0.923 | 1.271 | 1.415 | 0.905 |

| 0.680 | 0.936 | 0.968 | 0.783 | 0.937 | 0.748 | 0.863 | 0.751 | 0.698 | 0.868 |
Как и ожидалось, второй способ вычислений дал более точный результат.
3) По значениям, приведённым в таблицах (2.1) и (2.2) можно приближенно сосчитать дисперсии  для обоих методов расчёта:
для обоих методов расчёта:
для 1:

для 2:

Несмотря на то, что значение  невелико и приближенная нормальность оценки (2.2) не гарантирована, вычислим для обоих методов величины
невелико и приближенная нормальность оценки (2.2) не гарантирована, вычислим для обоих методов величины  . Получим значения 0.103 и 0.027. Также фактические абсолютные погрешности при расчёте
. Получим значения 0.103 и 0.027. Также фактические абсолютные погрешности при расчёте  , равные 0.048 и 0.016, – величины того же порядка. Точные же значения
, равные 0.048 и 0.016, – величины того же порядка. Точные же значения  в рассмотренном примере равны 0.233 и 0.0166. Таким образом, и при оценке дисперсий метод 2 оказался точнее метода 1.
в рассмотренном примере равны 0.233 и 0.0166. Таким образом, и при оценке дисперсий метод 2 оказался точнее метода 1.
Пример 2
Рассмотрим пример:
Требуется вычислить интеграл
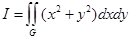 (3.4)
(3.4)
где область G задаётся следующими неравенствами: 
Область интегрирования принадлежит единичному квадрату  . Для вычисления интеграла воспользуемся таблицей случайных чисел (см. приложение), при этом каждые два последовательных числа из этой таблицы примем за координаты случайной точки
. Для вычисления интеграла воспользуемся таблицей случайных чисел (см. приложение), при этом каждые два последовательных числа из этой таблицы примем за координаты случайной точки  .
.
Записываем координаты  и
и  случайных точек в табл. 3.1, округляя до 3 знаков после запятой, и выбираем те из них, которые принадлежат области интегрирования.
случайных точек в табл. 3.1, округляя до 3 знаков после запятой, и выбираем те из них, которые принадлежат области интегрирования.
Заполним табл. 3.1 по правилу:
1) Среди всех значений  выделяем те, которые заключены между
выделяем те, которые заключены между  и
и  .Для этих значений полагаем
.Для этих значений полагаем  , для всех остальных
, для всех остальных 
2) Среди всех значений  . Соответствующих выделенным
. Соответствующих выделенным  , выбираем те, которые заключены между
, выбираем те, которые заключены между 
Для этих значений полагаем  , для всех остальных
, для всех остальных 
Таблица 3.1

| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 0.577 | 0.500 | 1.000 | 1 | 0.716 | 0 | 0.154 | 0 | 0 | |
| 0.737 | 0.500 | 1.000 | 1 | 0.701 | 0 | 0.474 | 0 | 0 | |
| 0.170 | 0.500 | 1.000 | 0 | 0.533 | 0 | ||||
| 0.432 | 0.500 | 1.000 | 0 | 0.263 | 0 | ||||
| 0.059 | 0.500 | 1.000 | 0 | 0.663 | 0 | ||||
| 0.355 | 0.500 | 1.000 | 0 | 0.094 | 0 | ||||
| 0.303 | 0.500 | 1.000 | 0 | 0.552 | 0 | ||||
| 0.640 | 0.500 | 1.000 | 1 | 0.205 | 0 | 0.280 | 1 | 1 | 0.452 |
| 0.002 | 0.500 | 1.000 | 0 | 0.557 | 0 | ||||
| 0.870 | 0.500 | 1.000 | 1 | 0.323 | 0 | 0.740 | 1 | 1 | 0.855 |
| 0.116 | 0.500 | 1.000 | 0 | 0.930 | 0 | ||||
| 0.930 | 0.500 | 1.000 | 1 | 0.428 | 0 | 0.860 | 1 | 1 | 1.048 |
| 0.529 | 0.500 | 1.000 | 1 | 0.095 | 0 | 0.058 | 0 | 0 | |
| 0.996 | 0.500 | 1.000 | 1 | 0.700 | 0 | 0.992 | 1 | 1 | 1.482 |
| 0.313 | 0.500 | 1.000 | 0 | 0.270 | 0 | ||||
| 0.653 | 0.500 | 1.000 | 1 | 0.934 | 0 | 0.306 | 0 | 0 | |
| 0.058 | 0.500 | 1.000 | 0 | 0.003 | 0 | ||||
| 0.882 | 0.500 | 1.000 | 1 | 0.986 | 0 | 0.764 | 0 | 0 | |
| 0.521 | 0.500 | 1.000 | 1 | 0.918 | 0 | 0.042 | 0 | 0 | |
| 0.071 | 0.500 | 1.000 | 0 | 0.139 | 0 | ||||
| всего | 4 | 3.837 | |||||||
3) Вычисляем  . Области тнтегрирования принадлежат только те точки, для которых
. Области тнтегрирования принадлежат только те точки, для которых  . В примере
. В примере 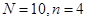
4) Вычисляем значения подынтегральной функции в полученных точках.
После заполнения табл. 3.1 вычисляем площадь области интегрирования  и по формуле (3.2) находим
и по формуле (3.2) находим 
Для сравнения приведём точное значение интеграла 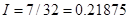
Результат имеет сравнительно небольшую точность потому, что число точек  недостаточно велико.
недостаточно велико.
Пример 3
Рассмотрим пример: найдём приближенно объём, ограниченный поверхностями
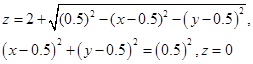
Искомый объём численно равен величине интеграла
 (3.7)
(3.7)
Так как в области V  , вводим новую переменную
, вводим новую переменную  , в результате чего интеграл (3.7) переходит в интеграл
, в результате чего интеграл (3.7) переходит в интеграл
 (3.8)
(3.8)
где  область, ограниченная поверхностями
область, ограниченная поверхностями

т.е.  принадлежит единичному кубу
принадлежит единичному кубу  .
.
Берём теперь три равномерно распределенные на отрезке  последовательности случайных чисел и записываем их в качестве координат
последовательности случайных чисел и записываем их в качестве координат  случайных точек в табл. 3.2. Затем проверяем, какие из этих точек принадлежат области
случайных точек в табл. 3.2. Затем проверяем, какие из этих точек принадлежат области  .
.
Таблица 3.2

| 
| 
| 
| 
| 
| 
| 
| 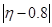
| 
| 
| 
|
| 1 | 0.577 | 0.116 | 0.077 | 0.384 | 0.147 | 1 | 0.667 | 1 | 1 | ||
| 2 | 0.716 | 0.930 | 0.216 | 0.430 | 0.232 | 0.993 | 0.193 | 0.231 | 0 | ||
| 3 | 0.737 | 0.930 | 0.237 | 0.430 | 0.241 | 1 | 0.242 | 1 | 1 | ||
| 4 | 0.701 | 0.428 | 0.201 | 0.072 | 0.045 | 0.940 | 0.140 | 0.122 | 1 | ||
| 5 | 0.170 | 0.529 | 0.330 | 0.029 | 0.110 | 1 | 0.610 | 1 | 1 | ||
| 6 | 0.533 | 0.095 | 0.033 | 0.405 | 0.165 | 1 | 0.131 | 1 | 1 | ||
| 7 | 0.432 | 0.996 | 0.068 | 0.496 | 0.251 | 0 | 0.352 | 1 | 0 | ||
| 8 | 0.263 | 0.699 | 0.237 | 0.199 | 0.096 | 1 | 0.645 | 1 | 1 | ||
| 9 | 0.059 | 0.313 | 0.441 | 0.187 | 0.229 | 1 | 0.646 | 1 | 1 | ||
| 10 | 0.663 | 0.270 | 0.163 | 0.230 | 0.080 | 1 | 0.680 | 1 | 1 | ||
| 11 | 0.355 | 0.653 | 0.145 | 0.153 | 0.046 | 1 | 0.577 | 1 | 1 | ||
| 12 | 0.094 | 0.934 | 0.406 | 0.434 | 0.353 | 0 | 0.716 | 1 | 0 | ||
| 13 | 0.303 | 0.058 | 0.197 | 0.442 | 0.234 | 1 | 0.737 | 1 | 1 | ||
| 14 | 0.552 | 0.003 | 0.052 | 0.497 | 0.250 | 1 | 0.701 | 1 | 1 | ||
| 15 | 0.640 | 0.882 | 0.140 | 0.382 | 0.165 | 1 | 0.169 | 1 | 1 | ||
| 16 | 0.205 | 0.986 | 0.295 | 0.486 | 0.323 | 0 | 0.533 | 1 | 0 | ||
| 17 | 0.002 | 0.521 | 0.498 | 0.021 | 0.248 | 1 | 0.432 | 1 | 1 | ||
| 18 | 0.557 | 0.918 | 0.057 | 0.418 | 0.178 | 1 | 0.263 | 1 | 1 | ||
| 19 | 0.870 | 0.071 | 0.370 | 0.429 | 0.318 | 0 | 0.059 | 1 | 0 | ||
| 20 | 0.313 | 0.139 | 0.187 | 0.361 | 0.185 | 1 | 0.663 | 1 | 1 | ||
|
| |||||||||||
Заполним табл. 3.2 по правилу:
1) выделяем точки, у которых 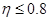 , и полагаем для них
, и полагаем для них 
2) среди выделенных точек области  принадлежат те, для которых выполняется неравенство
принадлежат те, для которых выполняется неравенство  .
.
Для этих точек 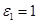 , для остальных
, для остальных 
3) вычисляем  . Области
. Области  принадлежат те точки, для которых
принадлежат те точки, для которых 
4) среди точек, у которых  , области
, области  принадлежат те точки, координаты которых удовлетворяют неравенству
принадлежат те точки, координаты которых удовлетворяют неравенству

Для этих точек  .
.
В примере общее количество точек  , а число точек, принадлежащих области
, а число точек, принадлежащих области  , равно 15. По формуле (3.6) получаем
, равно 15. По формуле (3.6) получаем
 , а точное значение объёма
, а точное значение объёма  равно
равно 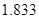
Погрешность формулы (3.6) обратно пропорциональна корню из числа испытаний, т.е.  .
.
Это означает, что для обеспечения большой точности число точек  должно быть очень велико. Но так как приближенные формулы (3.3), (3.6) не зависят от размерности интеграла, метод Монте-Карло оказывается выгодным при вычислении интегралов большой размерности.
должно быть очень велико. Но так как приближенные формулы (3.3), (3.6) не зависят от размерности интеграла, метод Монте-Карло оказывается выгодным при вычислении интегралов большой размерности.
Заключение
Процесс выполнения данной работы представлял большой интерес и послужил хорошей возможностью для приобретения новых знаний и навыков, а также закрепления уже полученных.
Были рассмотрены основные свойства метода Монте-Карло и создана программа, показывающая возможности данного метода при использовании ЭВМ.
Было выяснено, что методом Монте-Карло можно решать разнообразные задачи, в том числе вычисление интегралов, не прибегая к сложным математическим вычислениям. Простота алгоритма метода Монте-Карло позволяет успешно реализовывать их на ЭВМ.
Список литературы
1. Бусленко Н.П. Метод статистического моделирования – М.: Статистика, 1970. – 112 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1966. – 664 с.
3. Епанешников А.М., Епанешников В.А. Программирование в среде TURBO PASCAL 7.0 – М.: Диалог-МИФИ, 1998. – 288 с.
4. Ермаков С.М. Метод Монте-Карло и смежные вопросы – М.: Наука, 1975–472 с.
5. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 367 с.
6. Соболь И.М. Метод Монте-Карло – М.: Наука, 1985. – 80 c.
Приложения
1. Таблица 400 случайных цифр
| 86615 | 90795 | 66155 | 66434 | 56558 | 12332 | 94377 | 57802 |
| 69186 | 03393 | 42505 | 99224 | 88955 | 53758 | 91641 | 18867 |
| 41686 | 42163 | 85181 | 38967 | 33181 | 72664 | 53807 | 00607 |
| 86522 | 47171 | 88059 | 89342 | 67248 | 09082 | 12311 | 90316 |
| 72587 | 93000 | 89688 | 78416 | 27589 | 99528 | 14480 | 50961 |
| 52452 | 42499 | 33346 | 83935 | 79130 | 90410 | 45420 | 77757 |
| 76773 | 97526 | 27256 | 66447 | 25731 | 37525 | 16287 | 66181 |
| 04825 | 82134 | 80317 | 75120 | 45904 | 75601 | 70492 | 10274 |
| 87113 | 84778 | 45863 | 24520 | 19976 | 04925 | 07824 | 76044 |
| 84754 | 57616 | 38132 | 64294 | 15218 | 49286 | 89571 | 42903 |
2. Таблица 40 случайных чисел, равномерно распределенных на отрезке 
| 0.57705 | 0.35483 | 0.11578 | 0.65339 |
| 0.71618 | 0.09393 | 0.93045 | 0.93382 |
| 0.73710 | 0.30304 | 0.93011 | 0.05758 |
| 0.70131 | 0.55186 | 0.42844 | 0.00336 |
| 0.16961 | 0.64003 | 0.52906 | 0.88222 |
| 0.53324 | 0.20514 | 0.09461 | 0.98585 |
| 0.43166 | 0.00188 | 0.99602 | 0.52103 |
| 0.26275 | 0.55709 | 0.69962 | 0.91827 |
| 0.05926 | 0.86977 | 0.31311 | 0.07069 |
| 0.66289 | 0.31303 | 0.27004 | 0.13928 |
3. Листинг программы
Вычисляются значения кратных интегралов из примера 2–3.
program pmk;
uses crt;
var
w, u, h, k, v, y, p, s, g, x, x2, y2, z2, niu, Integral, Integral2:real;
n, m, i, a, b, e1, e2, e, e3, e4, e5:integer;
begin
clrscr;
writeln ('vychisleniye dvoynogo integrala iz primera 1');
writeln ('vvedite kolichestvo sluchaynykh tochek:');
readln(n);
for i:=1 to n do
begin
g:=random;
p:=random;
x:=g;
y:=p;
if ((0.5<=x) and (x<=1)) then e1:=1
else e1:=0;
if ((0<=y) and (y<=2*x-1)) then e2:=1
else e2:=0;
e:=e1*e2;
if e=1 then s:=s+x*x+y*y;
if e=1 then a:=a+1;
v:=1/4;
delay(1000);
end;
Integral:=(v/a)*(s);
writeln ('summa=', s:5:5);
writeln ('dvoynoy integral iz 1 primera =', Integral:5:5);
writeln ('vychisleniye troynogo integrala iz primera 2');
writeln ('vvedite kolichestvo sluchaynykh tochek:');
readln(m);
for i:=1 to m do
begin
w:=random;
u:=random;
h:=random;
x2:=w;
y2:=u;
niu:=h;
if niu<=0.8 then e3:=1;
if (x2–0.5)*(x2–0.5)+(y2–0.5)*(y2–0.5)<=(0.5)*(0.5) then e4:=1
else e4:=0;
e5:=e3*e4;
if (((0.8<niu) and (niu<1)) and ((x2–0.5)*(x2–0.5)+(y2–0.5)*(y2–0.5)+6.25*(niu-0.8)*(niu-0.8)<=(0.5)*(0.5))) then e5:=1;
if e5=1 then b:=b+1;
delay(1000);
end;
Integral2:=2.5*(b/m);
writeln ('kvo pod t =', b:5);
writeln ('troynoy integral iz 2 primera =', Integral2:5:5);
readln;
end.
4. Пример работы программы при 10000 случайных точек

|
из
5.00
|
Обсуждение в статье: Вычисление кратных интегралов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

