 |
Главная |
Теория вопроса и метод выполнения работы
|
из
5.00
|
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ПРОЗРАЧНОЙ ЖИДКОСТИ ПО МЕТОДУ СТОКСА
Цель работы: ознакомиться с методом определения коэффициента вязкости прозрачной жидкости методом движущегося в жидкости шарика.
Оборудование: стеклянный цилиндр, с прозрачной жидкостью; секундомер; микрометр; масштабная линейка; шарики из свинца.
Теория вопроса и метод выполнения работы
Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. К явлениям переноса относятся диффузия, внутреннее трение и теплопроводность.
Явлением внутреннего трения (вязкости) называется появление сил трения между слоями газа или жидкости, движущимся, друг относительно друга, параллельно и с разными по величине скоростями. Слой, движущийся быстрее, действует с ускоряющей силой на более медленно движущийся соседний слой. Силы внутреннего трения, которые возникают при этом, направлены по касательной к поверхности соприкосновения слоев (рис. 1, 2).
Величина силы внутреннего трения  между соседними слоями пропорциональна их площади
между соседними слоями пропорциональна их площади  и градиенту скорости
и градиенту скорости 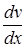 , то есть справедливо соотношение, полученное экспериментально Ньютоном
, то есть справедливо соотношение, полученное экспериментально Ньютоном
 .(1)
.(1)
Величина  называется коэффициентом внутреннего трения или динамическим коэффициентом вязкости. В СИ
называется коэффициентом внутреннего трения или динамическим коэффициентом вязкости. В СИ  измеряется в
измеряется в  .
.
Входящая в (1) величина 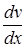 показывает, как меняется скорость жидкости в пространстве при перемещении точки наблюдения в направлении, перпендикулярном слоям. Понятие градиента скорости иллюстрируется рис. 1, 2.
показывает, как меняется скорость жидкости в пространстве при перемещении точки наблюдения в направлении, перпендикулярном слоям. Понятие градиента скорости иллюстрируется рис. 1, 2.

Рис. 1. Постоянный градиент скорости
На рисунке 1 показано распределение скоростей слоев жидкости между двумя параллельными пластинами, одна из которых неподвижна, а другая имеет скорость  . Подобная ситуация возникает в прослойке смазки между движущимися деталями. В этом случае слои жидкости, непосредственно прилегающие к каждой из пластин, имеют одинаковую с ней скорость. Движущиеся слои частично увлекают за собой соседние. В результате в пространстве между пластинами скорость жидкости меняется по направлению
. Подобная ситуация возникает в прослойке смазки между движущимися деталями. В этом случае слои жидкости, непосредственно прилегающие к каждой из пластин, имеют одинаковую с ней скорость. Движущиеся слои частично увлекают за собой соседние. В результате в пространстве между пластинами скорость жидкости меняется по направлению  равномерно. Таким образом, здесь
равномерно. Таким образом, здесь
 .
.
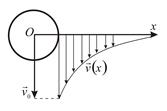
Рис. 2. Переменный градиент скорости
На рисунке 2 показано распределение скоростей жидкости около движущегося в ней вертикально вниз со скоростью  шарика.
шарика.
Предполагается, что скорость  мала, так что завихрения в жидкости не образуются. В этом случае жидкость, непосредственно прилегающая к поверхности шарика, имеет скорость
мала, так что завихрения в жидкости не образуются. В этом случае жидкость, непосредственно прилегающая к поверхности шарика, имеет скорость  . В это движение частично вовлекаются удаленные от шарика слои жидкости. При этом скорость наиболее быстро меняется по направлению
. В это движение частично вовлекаются удаленные от шарика слои жидкости. При этом скорость наиболее быстро меняется по направлению  вблизи шарика.
вблизи шарика.
Наличие градиента скорости у поверхности тела указывает, что на него действует сила внутреннего трения, зависящая от коэффициента вязкости  . Сама величина
. Сама величина  определяется природой жидкости и обычно существенно зависит от ее температуры.
определяется природой жидкости и обычно существенно зависит от ее температуры.
Сила внутреннего трения и коэффициент вязкости жидкости может быть определен различными методами – по скорости истечения жидкости через калиброванное отверстие, по скорости движения тела в жидкости и т.д. В данной работе для определения  используется метод, предложенный Стоксом.
используется метод, предложенный Стоксом.
Рассмотрим для примера равномерное движение маленького шарика радиуса  в жидкости. Обозначим скорость шарика относительно жидкости через
в жидкости. Обозначим скорость шарика относительно жидкости через  . Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рис. 2. В непосредственной близости к поверхности шара эта скорость
. Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рис. 2. В непосредственной близости к поверхности шара эта скорость  равна
равна  , а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии
, а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии  от поверхности шара.
от поверхности шара.
Очевидно, чем больше радиус шара, тем большая масса жидкости вовлекается им в движение, и  должно быть пропорционально радиусу шарика
должно быть пропорционально радиусу шарика  :
:  . Тогда среднее значение градиента скорости на поверхности шара равно
. Тогда среднее значение градиента скорости на поверхности шара равно
 .
.
Поверхность шара  , и полная сила трения, испытываемая движущимся шаром, равна
, и полная сила трения, испытываемая движущимся шаром, равна
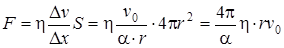 .
.
Более подробные расчеты показывают, что для шара  , окончательно
, окончательно 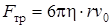 – формула Стокса.
– формула Стокса.
По формуле Стокса можно, например, определить скорости оседания частиц тумана и дыма. Ею можно пользоваться и для решения обратной задачи – измеряя скорость падения шарика в жидкости, можно определить ее вязкость.
Упавший в жидкость шарик движется равноускоренно, но, по мере того, как растет его скорость, будет возрастать и сила сопротивления жидкости до тех пор, пока сила тяжести шарика в жидкости не сравняется с суммой силы сопротивления и силы трения жидкости движению шарика. После этого движение будет происходить с постоянной скоростью  .
.
При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движение, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика. Таким образом, при вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.
Если шарик падает в жидкости, простирающейся безгранично по всем направлениям  , не оставляя за собой никаких завихрений (малая скорость падения, маленький шарик), то, как показал Стокс, сила сопротивления равна
, не оставляя за собой никаких завихрений (малая скорость падения, маленький шарик), то, как показал Стокс, сила сопротивления равна
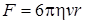 ,(2)
,(2)
где  – коэффициент внутреннего трения жидкости;
– коэффициент внутреннего трения жидкости;  – скорость шарика;
– скорость шарика;  – его радиус.
– его радиус.
Кроме силы  на шарик действует сила тяжести
на шарик действует сила тяжести  и архимедова сила
и архимедова сила  , равная весу
, равная весу  вытесненной шариком жидкости. Для шара
вытесненной шариком жидкости. Для шара
 ;
;  ,(3)
,(3)
где 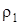 ,
,  – плотность материала шарика и исследуемой жидкости.
– плотность материала шарика и исследуемой жидкости.
Все три силы будут направлены по вертикали: сила тяжести – вниз, подъемная сила и сила сопротивления – вверх. Первое время, после вхождения в жидкость, шарик движется ускоренно. Считая, что к моменту прохождения шариком верхней метки скорость его уже установилась, получим
 ,
,
где 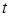 – время прохождения шариком расстояния между метками,
– время прохождения шариком расстояния между метками,  – расстояние между метками.
– расстояние между метками.
Движения шарика возрастает, ускорение уменьшается и, наконец, шарик достигнет такой скорости, при которой ускорение становится равным нулю, тогда
 .(4)
.(4)
Подставляя в равенство (4) значение величин, получим:
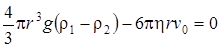 .(5)
.(5)
Решая уравнение (5) относительно коэффициента внутреннего трения, получаем расчетную формулу:
 .(6)
.(6)

Рис. 3. Прибор Стокса
На рисунке 3 представлен прибор, состоящий из широкого стеклянного цилиндра с нанесенными на него двумя кольцевыми горизонтальными метками  и
и 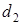 (
(  – расстояние между метками), который наполняется исследуемой жидкостью (касторовое масло, трансформаторное масло, глицерин) так, чтобы уровень жидкости был на 5¸8 см выше верхней метки.
– расстояние между метками), который наполняется исследуемой жидкостью (касторовое масло, трансформаторное масло, глицерин) так, чтобы уровень жидкости был на 5¸8 см выше верхней метки.
|
из
5.00
|
Обсуждение в статье: Теория вопроса и метод выполнения работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

