Задача 3. На использование Н-критерия Крускала-Уоллиса.

Решение

Индивидуальные показатели интеллекта по двум группам представлены в таблице 1, в порядке возрастания. Так как показатели в группе учащихся лицея выше, то эту группу считаем первой.

Таблица 1.

№ показателей	выборка 1 – учащиеся городского лицея	выборка 2 – учащиеся городской школы
1	130	125
2	128	125
3	127	121
4	127	112
5	127	112
6	126	100
7	124	88
8	124	84
9	112	82
10	112	78
11	100	72
12	100
13	99
14	94

Гипотезы к задаче

H ₀: Учащиеся лицея не превосходят учащихся школы по показателям интеллекта.

H ₁: Учащиеся лицея превосходят учащихся школы по показателям интеллекта.

Максимальный показатель во второй выборке – 125. Количество показателей первой выборки, ко­торые больше максимального показателя второй выборки: S ₁ = 6.

Минимальный показатель в первой выборке – 94. Количество показателей второй выборки, ко­торые меньше минимального показателя первой выборки: S ₂ = 5.

Эмпирическое значение критерия определяем по формуле:

Q _эмп = S ₁ + S ₂ = 6 + 5 = 11

По таблице определяем критические значения Q для n₁ = 14, n ₂ = 12:

«Ось значимости»

Ответ

Q _эмп =11, нулевая гипотеза отклоняется и принимается альтернативная гипотеза. Учащиеся лицея превосходят учащихся школы по показателям интеллекта ( a <0,01).

Задача 2. На использование U-критерия Манна-Уитни.

В двух классах средней общеобразовательной школе был проведен следующий эксперимент. В 7-«А» классе обучение велось по традиционной системе, в 7 «Б» — по программе «Развивающего обучения». По окончании эксперимента была проведена контрольная работа, которая дала результаты, показанные в таблице. Результаты контрольной работы оценивались по 10-бальной шкале. Необходимо определить, превосходят ли учащиеся 7 «Б» учащихся 7 «А» по уровню знаний.

                                                                                 Таблица 1

Ученик		1	2	3	4	5	6	7	8	9	10	11	12
Баллы	7–А	9	7	7	8	6	4	4	8	6	6	5	-
	7–Б	5	10	7	8	8	4	6	8	8	9	7	10

 

Решение. При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл.

Классы	Баллы	Ранги Б	Ранги А
Б	10	22,5
Б	10	22,5
А	9		20,5
Б	9	20,5
А	8		16,5
А	8		16,5
Б	8	16,5
Б	8	16,5
Б	8	16,5
Б	8	16,5
А	7		11,5
А	7		11,5
Б	7	11,5
Б	7	11,5
А	6		7,5
А	6		7,5
А	6		7,5
Б	6	7,5
А	5		4,5
Б	5	4,5
А	4		2
А	4		2
Б	4	2
Суммы		169	108

Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания.

Используя предложенный принцип ранжирования, получим таблицу рангов.

Чтобы использовать критерий Манна-Уитни, рассчитаем суммы рангов рассматриваемых выборок. Сумма для первой выборки равна 168,5, для второй – 107,5. Обозначим наибольшую из этих сумм через T_x (T_x=168.5). Среди объёмов n₁ и n₂ выборок наибольший обозначим n_x. Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:

T_x =168,5, n_x = 12 > 11 = n ₂ . Тогда:

Критическое значение критерия находим по прил. 1 и таблице.  Пусть уровень значимости равен 0.05.

Гипотеза H₀ о незначительности различий между баллами двух классов принимается, если U _кр < U _эмп . В противном случае H₀ отвергается и различие определяется как существенное.

Находим по таблице:

Соответствующая ось значимости имеет вид:

Следовательно, различия в уровне знаний по математике среди учащихся можно считать несущественными.

 

Задача 3. На использование Н-критерия Крускала-Уоллиса.

Четыре группы испытуемых выполняли тест Бурдона в разных экспериментальных условиях. Необходимо установить — зависит ли эффективность выполнения теста от условий или, иными словами, существуют ли статистически достоверные различия в успешности выполнения теста между группами. В каждую группу входило четыре испытуемых. Результаты выполнения теста приведены в следующей таблице:

 

№№	1 группа	2 группа	3 группа	4 группа
1	23	45	34	21
2	20	12	24	22
3	34	34	25	26
4	35	11	40	27
Сумма	112	102	123	96

 

Решение. Выдвигаем гипотезы:

Нулевая гипотеза H₀ :между показателями, измеренными в четырех разных условиях существует лишь случайные различия.

Альтернативная гипотеза H₁ :между показателями, измеренными в четырех разных условиях существует не только случайные различия.

Значения выборок объединяем в один ряд, упорядоченный по возрастанию.

Значения выборок ранжируем и ранги выписываем отдельно для каждой группы.

Находим для каждой группы сумму рангов и записываем в последний столбец таблицы.

 

	Данные	11	12	20	21	22	23	24	25	26	27	34	34	34	35	40	45
Ранги	Группа 1			3			6					12			14			35
	Группа 2	1	2										12				16	31
	Группа 3							7	8					12		15		42
	Группа 4				4	5				9	10							28

 

Общая сумма рангов 35+31+42+28 = 136, и по формуле

 следовательно, ранги проставлены правильно.

Вычисляем Н по формуле:

При определении критических значений критерия Н применительно к четырем и более выборкам используют таблицу для критерия хи-квадрат, подсчитав предварительно число степеней свободы v для с = 4.

Тогда v = с – 1=4 – 1=3 Находим по таблице:

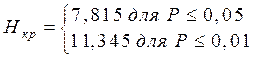
Соответствующая ось значимости имеет вид:

Полученное эмпирическое значение Н_эмп оказалось существенно меньше критического значения для 5% уровня. Следовательно, можно утверждать, что различий по показателю переключаемости внимания между группами нет.

     Переформулируем полученный результат в терминах нулевой и альтернативной гипотез: поскольку между показателями, измеренными в четырех разных условиях, существуют лишь случайные различия, то принимается нулевая гипотеза Н₀, т.е. гипотеза о сходстве. Иными словами, различные условия проведения теста Бурдона не влияют на показатели переключаемости внимания.

Замечание. Если использовать критерии, позволяющие сравнивать только два ряда значений, то полученный выше результат потребовал бы шести сравнений — первая выборка со второй, третьей и т.д.

 

Задача 4. На использование S-критерия тенденций Джонкира.

В выборке из 28 мужчин-руководителей проводилось обследование с помощью 16-факторного личностного опросника Р.Б. Кетелла (форма А). В таблице приведены индивидуальные значения испытуемых по фактору N. Данные сгруппированы по возрастным группам. Можно ли утверждать, что есть определенная тенденция изменения значений фактора N при переходе от группы к группе?

№№  испытуемых	1 группа	2 группа	3 группа	4 группа
	26-31год	32-37лет	38-42года	46-52года
1	2	11	8	11
2	10	7	12	12
3	5	8	14	9
4	8	12	9	9
5	10	12	16	10
6	7	12	14	14
7	12	9	10	13
Суммы	54	71	83	78
Среднее	7,71	10,14	11,86	11,14

Решение

Сначала необходимо проверить, есть ли возможность применить критерий Джонкира.

В данном случае количество групп (с) меньше 6, количество испытуемых в каждой группе ( n ) меньше 10, при этом все группы численно равны. Следовательно, критерий S применим.

Изменим последовательность расположения групп, упорядочив их по нарастанию значений фактора N, для чего придется поменять местами 4-ю и 3-ю группы.

Гипотезы к задаче

Н₀: Тенденция возрастания значений по фактору N при переходе от группы к группе в последовательности 1-2-4-3 является случайной.

Н₁: Тенденция возрастания значений по фактору N при переходе от группы к группе в последовательности 1-2-4-3 не является случайной.

Расчеты для нахождения эмпирического значения критерия отражены в таблице 1.

Таблица 1.

№№  испытуемых	Группа 1		Группа 2		Группа 4		Группа 3
	26-31год		32-37лет		46-52года		38-42года
	Значения	Кол-во более высоких значений справа	Значения	Кол-во более высоких значений справа	Значения	Кол-во более высоких значений справа	Значения
1	2	21	7	14	9	5	8
2	5	21	8	13	9	5	9
3	7	20	9	10	10	4	10
4	8	18	11	7	11	4	12
5	10	12	12	5	12	3	14
6	10	12	12	5	13	3	14
7	12	5	12	5	14	1	16
Суммы	54	109	71	59	78	25	83
Среднее	7,71	15,57	10,14	8,43	11,14	3,57	11,86

Определим величину A:  

Теперь определим величину B по формуле:

 

Определим эмпирическое значение S по формуле:

По таблице из Приложения 1 определим критические значения для данного количества групп (с=4) и данного количества испытуемых в каждой группе (n=7):

«Ось значимости»

Ответ

 S _эмп=92, Н₀ отклоняется. Тенденция возрастания значений по фактору N не является случайной (при a£0,05). Фактор N имеет тенденцию возрастать при переходе от первой группы ко второй, а затем к четвертой; самые высокие значения приходятся на третью возрастную группу.