Решение задач на построение методом инверсии

 

Сущность метода инверсии заключается в следующем.

Наряду с данными и искомыми фигурами рассматриваем фигуры, инверсные им или их частям. Иногда этого оказывается уже достаточно для нахождения таких связей между искомыми и данными, которые нужны для решения задачи. В большинстве случаев решение задачи сводится к построению фигуры, инверсной искомой, в предположении, что уже построена фигура, инверсная данной. Эта последняя задача, при удачном выборе базисной окружности, может оказаться проще данной задачи. Построив фигуру, инверсную искомой, затем строят искомую фигуру. Метод инверсии дает возможность решить ряд наиболее трудных конструктивных задач элементарной геометрии.

Недостатком этого метода является его громоздкость, связанная с необходимостью выполнить большое число построений.

Рассмотрим несколько примеров.

Пример 1. Через две данные точки А и В провести окружность, ортогональную данной окружности щ (О,r) (рис. 33).

Анализ. Если примем окружность щ за базисную окружность, то при инверсии искомая окружность г преобразуется в себя, а точки А и В перейдут в точки Аґ и Вґ на этой окружности. Но окружность г вполне определяется, если известны три точки на ней, например А, В и Аґ. Отсюда вытекает построение.

Построение.

1) Строим точку Аґ, инверсную точке А относительно окружности щ.

2) Строим окружность г, проходящую через точки А, В и Аґ. Г – искомая окружность.

Доказательство. Доказательство вытекает из анализа и построения.

Рис. 33

 

Исследование. Если точка А лежит на окружности щ, то точка Аґ совпадает с точкой А и указанный путь решения непригоден. В этом случае нужно провести аналогичное построение относительно точки В. если обе точки А и В лежат на окружности щ, то построение можно выполнить так: через А и В проводим касательные к окружности щ и отмечаем точку их пересечения О1. О1 – центр искомой окружности.

Эти построения непригодны, если точки А, В и О расположены на одной прямой. Если при этом точки А и В не инверсны, то задача не имеет решения. Если же точки А и В инверсны относительно окружности щ, то задача имеет бесконечное множество решений: любая окружность, проходящая через точки А и В, ортогональна окружности щ.

Пример 2. Даны: точка О и две не проходящие через нее прямые a и b. Провести через точку О такой луч, чтобы произведение его отрезков от точки О до точек пересечения с данными прямыми было равно квадрату данного отрезка.

Анализ. Пусть О – данная точка, а и b – данные прямые, ОАВ – искомый луч, так что ОА 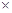ОВ = r2, где r – данный отрезок (рис. 34).

Рис. 34

 

Инверсия относительно окружности щ (О, r) переведет точку А в точку В, а прямую а – в некоторую окружность аґ, проходящую через точку В. таким образом, В ≡ аґ*b.

Построение. Строим последовательно:

1) Окружность щ (О, r);

2) Образ аґ прямой а в инверсии относительно щ;

3) Точку В ≡ аґ*b;

4) Луч ОВ, который и удовлетворяет условию задачи.

Доказательство. Пусть А ≡ ОВ а. Тогда А – прообраз точки В в инверсии относительно щ (О, r), так как прямая а – прообраз окружности аґ. Следовательно, по определению инверсии, ОА 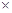ОВ = r2.

Исследование. Возможны следующие случаи:

1) окружность аґ пересекает прямую b; два решения;

2) окружность аґ касается прямой b; одно решение;

3) окружность аґ не имеет общих точек с прямой b; решений нет.

Так как искомая точка В обязательно соответственна точке А в инверсии относительно щ (О, r), то точка В должна быть общей точкой прямой b и окружности аґ. Отсюда следует, что других решений, кроме найденных, задача не может иметь.

Пример 3. Построить окружность, касательную к данной окружности г и проходящую через две данные точки А и В вне данной окружности.

Анализ. Пусть б (рис. 35) – искомая окружность. Желательно преобразовать фигуру так, чтобы окружность б (или окружность г) преобразовалась в прямую.

 

Рис. 35

 

С этой целью примем точку В за центр инверсии, а отрезок ВА – за радиус инверсии. Тогда окружность г преобразуется в некоторую окружность гґ, точка А преобразуется в себя, искомая окружность б – в прямую бґ. Прямая бґ должна пройти через точку А, а также касаться окружности гґ, так как окружность б касается окружности г (рис. 36). Таким образом, задача сводится к построению касательной из построенной точки (Аґ) к построенной окружности (гґ).

Построение. Строим последовательно:

1) Окружность щ с центром в точке В радиуса ВА;

2) Окружность гґ, инверсную окружности г относительно окружности щ;

3) Прямую бґ, проходящую через точку А и касающуюся окружности гґ;

4) Окружность б, инверсную прямой бґ относительно окружности щ. Окружность б искомая.

Рис. 36

 

Доказательство. Прямая бґ касается окружности гґ, поэтому соответствующая ей окружность б касается соответственной окружности г. Прямая бґ проходит через точку А, и поэтому окружность б проходит через ту же точку; во всех случаях, когда прямая бґ не проходит через центр инверсии, то есть через точку В.

Исследование. Из четырех шагов построения шаги 1) и 2) всегда выполнимы, притом однозначно. Рассмотрим построение 3).

Проведение касательной к окружности гґ через точку А зависит от расположения точки А относительно окружности гґ. Можно допустить три предположения: а) точка А на окружности гґ; б) точка А внутри окружности гґ; в) точка А вне окружности гґ.

Случай а) невозможен, так как из Аґ Є гґ следовало бы А Є г, что противоречит условию задачи.

Докажем, что случай б) также невозможен. Применим для этого доказательство «от противного». Допустим, что точка А располагается внутри окружности гґ (рис. 37). Так как точка В, по условию, вне г, то В также вне гґ (это следует из способа построения окружности гґ). Поэтому луч ВАґ встретит окружность гґ в двух точках, причем одна из них внутри окружности щ, а другая вне ее. Обозначим внутреннюю точку пересечения через Рґ, а внешнюю – через Qґ. При инверсии точки Рґ, Qґ и Аґ преобразуются в точки Р, Q и А, причем Q внутри щ, Р вне щ, А на щ, так что А лежит между Р и Q. Окружность гґ, проходящая через Рґ и Qґ, перейдет в окружность г, проходящую через Р и Q. И так как точка А принадлежит хорде РQ окружности г, то А внутри г, вопреки условию задачи.

Таким образом, возможен лишь случай в), то есть А вне гґ. Поэтому из точки А всегда можно провести две касательные к окружности гґ.

Перейдем к четвертому шагу. При инверсии прямая бґ преобразуется в окружность лишь в том случае, когда эта прямая не проходит через центр инверсии. Если же прямая бґ проходит через точку В, то прямая ВА касательная к окружности бґ. Но при инверсии прямая ВА преобразуется в себя, а окружность гґ - в окружность г. Следовательно, если прямая бґ проходит через точку В, то окружность г касается прямой ВА (и наоборот). В этом последнем случае прямая бґ инвертируется в прямую. Таким образом, приходим к следующему выводу: при данном способе построения мы получаем единственное решение, если прямая АВ касается окружности г, и два решения во всяком другом случае.

 

Рис.37

 

Решая задачу каким-либо иным способом, мы не получим новых решений. В самом деле, если бы задача имела более одного решения в случае, когда АВ касается г, или более двух решений в любом ином случае, то после инверсии относительно окружности щ оказалось бы, что через точку Аґ (Аґ ≡ А) проходило бы не менее трех касательных к окружности гґ, что невозможно.

Заметим, что данную задачу можно решить, принимая за центр инверсии точку на данной окружности г. При этом задача сводится к следующей: построить окружность, касающуюся данной прямой и проходящую через две данные точки. Эта задача может быть решена без привлечения метода инверсии.

 

Задача Аполлония

 

Методом инверсии может быть решена в общем случае задача Аполлония о касании окружностей:

Построить окружность, касающуюся трех данных окружностей.

Эта задача впервые была решена известным греческим геометром Аполлонием Пергским в III в. до н. э. в сочинении, которое до нас не дошло, но о котором упоминают некоторые древние математики (например, Папп). Способ, с помощью которого решил эту задачу Аполлоний, неизвестен. Многие задачи из числа рассматриваемых в школьном курсе геометрии представляют частные или предельные случаи задачи Аполлония. Частные случаи возникают при специальном расположении данных окружностей, предельные – когда все или некоторые из данных окружностей вырождаются в точки (радиус окружностей неограниченно уменьшается) или прямые (радиус неограниченно возрастает).

Прежде, чем решить задачу Аполлония в общем случае, рассмотрим некоторые частные и предельные случаи.

Задача 1. Построить окружность, проходящую через три данные точки.

Решение общеизвестно.

Задача 2. Построить окружность, касающуюся трех данных прямых. Решение этой задачи также общеизвестно. Она может иметь до четырех решений.

Задача 3. Построить окружность, проходящую через данную точку и касающуюся двух данных параллельных прямых.

Анализ. Пусть дана точка Р и и две параллельные прямые а и b. Обозначим расстояние между данными прямыми через d. Тогда радиус искомой окружности должен быть равен d/2. задача сводится к построению центра окружности, который должен удовлетворять двум условиям: 1) он должен быть одинаково удален от прямых а и b; 2) он должен отстоять от точки Р на расстоянии d/2. отсюда вытекает построение.

Построение.

1. АВ ┴ b, А Є а;

2. С Є АВ, АС = СВ;

3. с – прямая, С Є с, с ║а, с ║b;

4. щ (Р, d/2);

5. О1 = щ ∩ с;

6. щ1 (О1, О1Р) – искомая.

 

Рис. 38

 

Доказательство. Окружность щ1 касается прямых а и b, так как расстояния ее центра О1 от этих прямых одинаковы и равны d/2. эта окружность проходит через точку Р по построению.

Исследование. Возможны три случая.

1. Точка р расположена между данными прямыми а и b. Указанный способ построения дает два решения: щ1 (О1, О1Р) и щ2 (О2, О2Р). Других решения нет, ибо если бы существовали три окружности, удовлетворяющие условиям задачи, то их центры О1, О2 и О3 должны были бы лежать на одной прямой с. С другой стороння, мы должны были бы иметь О1Р = О2Р = О3Р = АС, то есть точки О1, О2 и О3 должны были бы лежать на одной окружности (Р, АС), так что возникает противоречие.

2. Точка Р - на одной из прямых а или b. Задача имеет одно решение.

3. Точка Р – вне полосы, ограниченной прямыми а и b. Задача не имеет решений.

Задача 4. Построить окружность, проходящую через две данные точки и касающуюся данной прямой.

Эта задача может быть решена методом инверсии, если за центр инверсии принять одну из данных точек, а ее расстояние до данной прямой принять за радиус инверсии. Она может быть решена и без инверсии.

Задача 5. Построить окружность, касающуюся данной окружности и проходящую через две данные точки. Эта задача решена в предыдущем пункте в предположении, что данные точки расположены вне данной окружности. В других случаях решение аналогично или еще проще.

Задача 6. построить окружность, касающуюся трех данных окружностей, проходящих через одну общую точку Р.

Если принять общую точку трех данных окружностей г1, г2 и г3 за центр инверсии, то эти окружности преобразуются в три прямые. Таким образом, задача сводится к построению окружности, касающейся трех построенных прямых. Искомая окружность – образ этой окружности в данной инверсии.

Переходим к решению задачи Аполлония в общем случае, причем остановимся лишь на основных моментах этого решения, не вникая в отдельные его детали.

Решение, которое мы дадим, основано на предварительном решении двух вспомогательных задач (представляющих предельный и частный случаи общей задачи).

1-я вспомогательная задача: построить окружность, касающуюся двух параллельных прямых и данной окружности.

Задача обычно решается методом геометрических мест. Пусть а и b – данные прямые, г (О, r) – данная окружность (рис. 39).

 

Рис. 39

 

Из произвольной точки А на прямой а опускаем перпендикуляр АВ на прямую b. Через середину С отрезка АВ проводим прямую с параллельно а. строим окружность д (О, r + АС) (или радиуса │r - АС│). Отмечаем точку пересечения этой окружности с прямой с; это и будет центр искомой окружности.

Эта задача может иметь до четырех различных решений.

2-я вспомогательная задача: построить окружность, касающуюся трех данных окружностей, если две из них взаимно касаются.

Эта задача решается методом инверсии. Пусть г1, г2 и г3 – данные окружности, причем г1 и г2 касаются в точке Т (рис. 40).

Рис. 40

 

Примем точку Т за центр инверсии, а за радиус инверсии – произвольный отрезок (удобно избрать его так, чтобы базисная окружность щ пересекла окружности г1 и г2). При инверсии окружности г1 и г2 преобразуются в пару параллельных прямых гґ1 и гґ2, а окружность г3 – в некоторую окружность (или прямую) гґ3. построить окружность гґ, касающуюся прямых гґ1 и гґ2 и линии гґ3, мы умеем (см. 1-ю вспомогательную задачу). При инверсии этой окружности она преобразуется в окружность (или прямую) г, которая будет касаться трех данных окружностей г1, г2 и г3.

Решение задачи Аполлония в общем случае сводится к этой 2-й вспомогательной задаче. Мы воспользуемся для этого приемом, иногда называемым «методом расширения».

Для определенности рассмотрим тот случай, когда каждая из трех данных окружностей расположена вне двух других (рис. 41).

Рис. 41

 

В других случаях решение проводится аналогично.

Пусть г1 (О1, r1), г2 (О2, r2) и г3 (О3, r3) –данные окружности. Пусть, далее, прямая О1О2 пересекает окружность г1 в точках А1 и Аґ1, а окружность г2 – в точках А2 и Аґ2. из четырех отрезков А1А2, Аґ1Аґ2, Аґ1А2 и А1Аґ2 выберем кратчайший. Пусть это будет отрезок А1А2. обозначим через Т его середину. Увеличим радиусы всех данных окружностей на отрезок А1Т, то есть построим окружности гґ1 (О1, r1 + А1Т), гґ2 (О2, r2 + А1Т), гґ3 (О3, r3 + А1Т). из них окружности г1 и гґ2 касаются в точке Т. мы можем теперь построить окружность гґ, касающуюся трех окружностей гґ1, гґ2 и гґ3 (см. 2-ю вспомогательную задачу). Обозначим центр окружности гґ через О, а радиус - через rґ. Если затем построить концентрическую ей окружность г (О, rґ + А1Т), то эта последняя будет касаться трех данных окружностей.

Число всех возможных решений задачи Аполлония зависит от взаимного расположения данных окружностей. Приведем без доказательства несколько примеров.

1. Если окружность г2 расположена внутри окружности г1, а окружность г3 вне окружности г1 (рис. 42), то задача Аполлония вовсе не имеет решения. Это относится в частности, и к случаю, когда все три данные окружности концентрические.

2. Если две окружности г1 и г2 касаются, а третья окружность г3 пересекает их в точке их касания, то задача Аполлония имеет два решения Г1 и Г2 (рис. 43).

3. Если каждая из данных окружностей расположена вне двух других, причем касательная к каждым двум из данных окружностей не имеет обшей точки с третей окружностью, то задача имеет восемь решений (рис. 44).

4. Если три данные окружности попарно касаются в одной точке, то можно провести бесконечно много окружностей, касающихся каждой из данных (рис. 45).

 

Рис. 42

Рис. 43

 

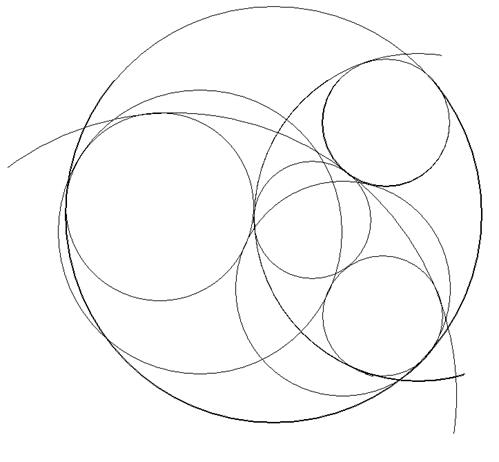
Рис. 44

Рис. 45

 

Полное исследование показывает, что если задача Аполлония имеет лишь конечное число решений, то их не более восьми.

Приложение.

Рассмотрим некоторые задачи, для решения которых используется понятие и метод инверсии.

Задача 1. Дан квадрат, две вершины которого лежат на окружности инверсии, а третья – в центре инверсии. Построить фигуру, ему инверсную.

Анализ. Пусть щ (О, R) – базисная окружность, ОАВС – данный квадрат. Точка А Є щ, точка С Є щ. При инверсии точка А переходит в точку Аґ, точка С – в Сґ, точка В – в Вґ, а ОС переходит в прямую ОL∞, ОА – в ОК∞, АВ переходит в дугу m, СВ переходит в дугу n. Таким образом, фигура определяется как СґnВґmАґВ, которая является инверсией квадрата ОАВС.

 

Рис. 1

Построение. (рис. 1).

1. щ (О, R) базисная окружность;

2. В → Вґ, А ≡ Аґ, С ≡ Сґ;

3. СВ → СnВґ;

4. АВ → АґmВґ;

5. СґnВґmАґВ – искомая фигура.

Доказательство. Доказательство следует из анализа и построения.

Исследование. Задача всегда имеет решение и притом единственное.

Задача 2. Дан квадрат, однв вершина которого совпадает с центром инверсии, а противоположная вершина лежит на окружности инверсии. Построить фигуру, ему инверсную.

Анализ. Пусть щ (О, R) – базисная окружность, ОАВС – данный квадрат, В Є щ. При инверсии точка В переходит в точку Вґ, В ≡ Вґ, точка А переходит в точку Аґ, Аґ  l, В  l, точка С переходит в точку Сґ, Сґ  l. АВ переходит в дугу АґmB окружности щ1 (А, ОА), ВС переходит при инверсии в дугу СґnВ окружности щ2 (С, ОС). ОА – часть луча, поэтому при инверсии ОА преобразуется во внешнюю его часть АґК∞, а ОС – в СґL∞. Таким образом, инверсная фигура определяется как К∞АґmВґnСґL∞.

Построение. (рис. 2)

1. щ (О, R) – базисная окружность;

2. В ≡ Вґ, А ≡ Аґ, С ≡ Сґ, В  l, Аґ  l, Сґ  l;

3. АВ → АґmBґ;

4. ОС → ВґnCґ;

5. ОА → АґК∞;

6. ОС → СґL∞;

7. К∞АґmВґnСґL∞ - искомая фигура.

Доказательство. Доказательство следует из анализа.

Рис. 2

 

Исследование. Задача всегда имеет решение и притом единственное.

Задача 3. Построить фигуру, инверсную окружности, концентрической базисной.

Анализ. Пусть щ (О, Р) – базисная окружность инверсии, щ1 (О1, R1) – данная окружность. Так как окружность щ (О, R1) не проходит через центр инверсии, то преобразуется в окружность. Для построения искомой окружности надо найти точки Аґ и Вґ - инверсные точкам А и В, где А и В – диаметрально противоположные точки, а отрезок АґВґ - являются диаметром искомой окружности.

Построение.

1. щ (О, Р) базисная окружность, щ1 (О1, R1) – данная окружность, причем R1 ≠ R2;

2. О  m – произвольная прямая;

3. А = m 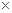щ1, В = m щ2;

4. Точка Аґ - инверсна точке А, Вґ - Инверсна точке В;

5. щ1ґ (О, ) – искомая окружность (рис 3).

Доказательство следует из анализа.

Рис 3

 

Исследование. Задача всегда имеет единственное решение.

Задача 4. Точка описывает хорду базисной окружности, отличную от диаметра. Построить линию, которую описывает инверсная точка.

Анализ. Пусть щ (О, Р) – базисная окружность инверсии, АВ – хорда, причем О АВ. Точка М описывает хорду АВ.

Заметим, что А = Аґ, В = Вґ. Прямая АВ не проходит через центр О, значит преобразуется в окружность щ1, которая проходит через центр.

Но так как дана не вся прямая, а только хорда АВ, то она преобразуется в дугу относительно окружности щ1 (концы дуг А и В), причем, во внешнюю дугу относительно окружности щ (О, Р), так как данная точка М расположена внутри окружности щ (О, Р).

Построение.

1. щ (О, Р), АВ – данная хорда;

2. щ1 – окружность, которая проходит через точки О, А, В;

3. АmВ – внешняя относительно щ, которая является искомой фигурой (рис. 4).

Рис 4

 

Доказательство следует из анализа.

Исследование. Задача всегда имеет единственное решение.

Задача 5. Найти такую точку, чтобы касательные, проведенные из нее к двум данным окружностям были равны ее расстоянию от данной точки.

Анализ. щ1 (О1, R1), щ2 (О2, R2) – данные окружности. Пусть точка А – искомая, тогда АК = АМ = АN. АК – касательная к щ1, АМ – касательная к щ2, то есть точка А а12 – радикальная ось окружности щ1 и щ2 и А а20 – радикальная ось щ2 и точки N, отсюда следует, что А = а12  а20.

Построение.

1. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, N – данная точка;

2. а12 – радикальная ось щ1 и щ2;

3. а20 – радикальная ось щ2 и N;

4. А = а12  а20, А – искомая точка (рис. 5).

Рис. 5

 

Доказательство. Точка А – радикальный центр щ1, щ2 и N.

Исследование.

1. Если щ1 и щ2 - концентрические, то задача не имеет решения.

2. Если N внутри щ1 (О1, R1) или щ2 (О2, R2), то решений нет.

3. Если радкальные оси параллельны, то решений нет.

4. Если радикальные оси совпадают, то задача имеет бесконечное множество решений.

Задача 6. Построить фигуру, инверсную сектору базисной окружности.

Анализ. Пусть щ (О, R) – данная базисная окружность, АmВО – данный сектор.

При инверсии точка А переходит в точку Аґ, часть луча ОА переходит во внешнюю его часть АґК∞. дуга АmВ при инверсии преобразуется в себя.

Точка В преобразуется в точку Вґ. ОВ преоюразуется в ВґL∞. Таким образом сектор базисной окружности АmВО преобразуется в фигуру, определяемую внешней частью луча, АґК∞, ВґL∞ и дугой АґmВґ.

Построение.

1. щ (О, R) – базисная окружность;

2. А ≡ Аґ, В ≡ Вґ;

3. ОА → АґК∞;

4. ОВ → ВL∞;

5. АmВ → АґmВґ;

6. К∞АґmВґL∞ - искомая фигура (рис. 6).

Доказательство. Доказательство следует из анализа и построения.

Исследование. Задача имеет всегда решение и притом единственное.

 

Рис. 6

 

Задача 7. Даны две окружности, касающиеся друг друга в точке А. приняв точку А за полюс инверсии построить фигуру, инверсную двум окружностям.

Анализ. Пусть щ1 (О1, R1), щ2 (О2, R2) – данные окружности, щ (А, R) - базисная окружность. В = щ щ2, С = щ щ2, D = щ щ1, К = щ щ1. при инверсии точки В, С, D и К преобразуются в себя, так как они принадлежат щ (А, R). Так как окружности щ1 и щ2 проходят через центр базисной окружности, то они преобразуются в прямые : l1 B, l1  C, l2 D, l2  К.

Построение.

1. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, щ1  щ2 = А, щ (А, R) - базисная окружность;

2. В = В = щ щ2, В → Вґ;

С = С = щ щ2, С → Сґ;

3. D = щ щ1, D → Dґ;

К = К = щ щ1, К → Кґ;

4. l1  Вґ, l1 Сґ, l2  Dґ, l2  Кґ, l1 и l2 – искомые прямые (рис 7).

 

Рис. 7

 

Доказательство.Доказательство следует из анализа и построения.

Исследование. Задача имеет единственное решение.

Задача 8. через данную точку А провести окружность, ортоганальную двум данным окружностям.

Анализ. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, точка А - данная точка.

Примем щ1 и щ2 за базисные, тогда точка А при инверсии преобразуется в точку Аґ, Аґ О1А, и А преобразуется Аґґ, Аґґ О2А.

А, Аґ, Аґґ щ (О, ОА), щ – искомая окружность.

Построение.

1. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, А – данная точка;

2. А → Аґ, Аґ О1А;

3. А → Аґґ, Аґґ О2А;

4. А, Аґ, Аґґ щ (О, ОА);

щ (О, ОА) – искомая окружность (рис. 8).

Рис. 8

 

Доказательство. Окружность, проходящая через три взаимноинверсные точки, ортоганальна двум данным окружностям. А, Аґ, Аґґ - взаимноинверсные точки.

Исследование. Задача имеет единственное решение.

Задача 9. Зная радиус инверсии, расстояние двух точек А иВ от центра инверсии и расстояние АВ, вычислить расстояние между точками Аґ и Вґ, соответственно инверсными точкам А и В.

Анализ. щ (О,R) – базисная окружность, А и В – данные точки. ОА = а, ОВ = b, АС = с. При инверсии точка А преобразуется в точку Аґ, В преобразуется в Вґ.

Из подобия треуголиников ОАВ и ОАґВґ следует, что , АґВґ = ; ОАґ 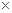ОА = R2; ОАґ = , АґВґ = 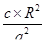 (рис. 9).

 

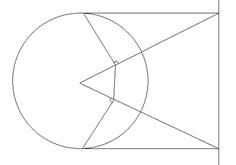
Рис. 9

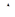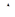Доказательство. Доказательство следует из свойств взаимноинверсных точек А и Аґ, В и Вґ и подобия ОАВ и ОАґВґ.

Исследование. Задача имеет единственное решение.

Задача 10. Даны окружность щ1 (О1, R1) и прямая l. Построить окружность инверсии щ (О, R), относительно которой щ1 (О1, R1) и прямая l были бы взаимноинверсны.

Анализ. щ1 (О1, R1) – данная окружность, l – данная прямая. m – произвольная прямая, m l. А m, А l.

При инверсии точка А преобразуется в точку Аґ, Аґ щ1, Аґ = щ1  m. l ║lґ, lґ  m, lґ А. О = m  щ1, В = щ2 (О2, )  lґ.

ОВ – радиус искомой окружности инверсии.

Построение.

1. щ1 (О1, R1) – данная окружность, l – данная прямая;

2. m l, m – произвольная прямая, m  l = А, m щ1 = О;

3. l ║lґ, lґ  m, Аґ lґ;

4. щ2 (О2, );

5. В = щ2 lґ;

6. щ (О, ОВ) – искомая окружность (рис. 10).

 

Рис. 10

Доказательство. Так как по условию щ1 (О1, R1) и прямая l взаимноинверсны, то щ1 (О1, R1) проходит через центр окружности инверсии, значит взяв произвольную точку А l, мы должны построить касательную к искомой окружности в точке В. АґВ О1Аґ, О1А, Аґ принадлежит одной прямой m.

Исследование. Задача имеет единственное решение.

Задача 11. Дана окружность щ (О, R) и АВС, где А, В, С щ. Построить фигуру, инверсную вписанному треугольнику АВС.

Анализ. АВС – данный треугольник, А, В, С щ (О, R). При инверсии точки, принадлежащие базисной окружности преобразуется в себя, то есть А ≡ Аґ, В ≡ Вґ, С ≡ Сґ. Прямая, не проходящая через центр инверсии преобразуется в окружность, проходящую через центр инверсии, то есть АВ преобразуется в дугу АmВ окружности г1, ВС преобразуется в дугу ВnС окружности г2, АС преобразуется в дугу АkС окружности г3. таким образом АВС преобразуется при инверсии в три дуги.

Построение.

1. щ (О, R) – базисная окружность,  АВС, А,В,С щ;

2. А ≡ Аґ, В ≡ Вґ, С ≡ Сґ;

3. АВ → АmВ, АmВ г1 (О, R1),

ВС → ВnС, ВnС  г2 (О, R2),

АС → АkС, АkС  г3 (О, R3);

4. АґmВґnCґkAґ - искомая фигура (рис 11).

Доказательство.

Доказательство следует из анализа.

Исследование.

Задача всегда имеет решение и притом единственное.

Рис 11

 

Задача 12. Даны точка О и две не проходящие через нее прямые а и b. Провести через точку О такой луч, чтобы произведение его отрезков от точки О до точек пересечения с данными прямыми было равно квадрату данного отрезка.

Анализ. Пусть точка О – данная точка, а и b – данные прямые, ОВ - искомый луч, такой что ОА 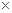ОВ = r2, где r – данный отрезок.

Инверсия относительно окружности щ (О, r) переведет точку А в точку В, а прямую а – в некоторую окружность г, проходящую через точку В. Таким образом, В ≡ г b.

Построение.

1. щ (О,r) – базисная окружность;

2. а → г;

3. В ≡ г  b;

4. ОВ – искомый луч (рис 12).

 

Доказательство.

Пусть А = ОВ  а, тогда А – прообраз точки В в инверсии относительно щ (О, r), так как прямая а – прообраз окружности г, то по определению инверсии ОА 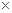ОВ = r2.

Исследование.

1. Если г  b, то задача имеет два решения;

2. Если окружность г касается b, то задача имеет одно решение;

3. Если г не пересекается с b, то решений нет.

Заключение

 

Геометрические построения могут сыграть серьезную роль в математической подготовке школьника. Задачи на построение, решаемые с помощью инверсии обычно не допускают стандартного подхода к ним и формального восприятия их учащимися. Такие задачи удобны для закрепления теоретических знаний учащихся по любому разделу школьного курса геометрии. Решая геометрические задачи на построение, учащиеся приобретают много полезных чертежных навыков.

В данной работе было рассмотрено понятие инверсии как метода, с помощью которого решаются некоторые задачи на построение, рассмотрены основные свойства и теоремы, на которые опирается данный метод. Также в дипломной работе рассмотрена задача Аполлония, решение которой и является основой метода инверсии, приведены примеры решения задач на построение с помощью инверсии. В приложении дипломной работы представлены решения некоторых более сложных задач.

Данная тема, на мой взгляд, подходит к проведению факультативных занятий по геометрии в 8 классе, т. к. в 7 классе были изучены основные моменты планиметрии, которые необходимо знать для решения задач на построение, но при этом следует для начала провести курс по изучению темы инверсии. Это имеет место, так как в это время лучше всего нужно развивать мыслительную деятельность учеников, учить ребят доказывать, размышлять, развивать основные навыки, необходимые для дальнейшего лучшего усвоения геометрии. Но это важно еще и потому, что на решение таких задач в курсе планиметрии практически нет времени.

Геометрические построения в настоящее время не связаны непосредственно с наиболее актуальными проблемами математики. Но в процессе изучения усваиваются понятия и приобретаются некоторые навыки, имеющие значения и за пределами этого вопроса. Одним из широко распространенных в современной математике понятий является понятие алгоритма. Изучение геометрических построений является хорошим средством подготовки к усвоению этого понятия. Действительно, цель решения каждой геометрической задачи как раз и состоит в получении некоторого алгоритма. Разрешимость геометрической задачи на построение понимается именно как алгоритмическая разрешимость. Весьма поучительно рассмотрение задач, связанных с доказательством невозможности выполнения какого-либо построения данными средствами, так как вопросы разрешимости той или иной задачи при тех или иных допущениях встречающихся в самых различных разделах математики. Геометрические построения играют также особую роль, как средство доказательства существования геометрической фигуры обладающей указанными свойствами. Геометрические построения составляют также теоретическую основу практической графики.

Список используемой литературы

 

1. А. Адлер, Теория геометрических построений, М., Учпедгиз, 1940;

2. Б. И. Аргунов, М. Б. Балк, Геометрические построения на плоскости, изд. 2, Учпедгиз, 1957;

3. Н. Ф. Четверухин, Методы геометрических построений, М., Учпедгиз, 1952;

4. Б. И. Аргунов, М. Б. Балк, Элементарная геометрия, М., Просвещение, 1966;

5. А. В. Погорелов, Геометрия, изд.2, М., Наука, 1984;

6. И. Я. Бакельман, Инверсия;

7. С. Л. Певзнер, Инверсия и ее приложения, Хабаровск, 1988;

8. И. М. Яглом, Геометрические преобразования, Т.П.М., Гостехиздат, 1956;

9. Д. И. Перепелкин, Курс элементарной геометрии, И.Г.М., Гостехиздат, 1948;

10. Б.В. Кутузов, Геометрия. Пособие для учительских и педагогических институтов, М., Учпедгиз, 1950;

11. П. С. Моденов, А. С. Пархоменко, Геометри<