 |
Главная |
Теорема о непрерывности, произведения частного функций в точке (формулировка, доказательство).
|
из
5.00
|
Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции, теоремы об эквивалентных бесконечно малых функциях (с доказательством одной из них).
Сравнение бесконечно малых функций:
1. Функция  называется бесконечно малой при
называется бесконечно малой при  (или в точке х=а), если
(или в точке х=а), если 
Пример. Функция  яляется бесконечно малой при
яляется бесконечно малой при 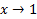 , так как
, так как 
2. Бесконечно малые функции одного порядка
Функции  и
и 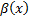 называются бесконечно малыми одного порядка малости при
называются бесконечно малыми одного порядка малости при  , если
, если 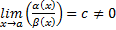
3. Бесконечно малые функции более низкого и высокого порядков
Если  , то
, то  является бесконечно малой более высокого порядка при
является бесконечно малой более высокого порядка при  , чем
, чем 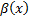 , а
, а 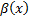 – бесконечно малой более низкого порядка по сравнению с
– бесконечно малой более низкого порядка по сравнению с  :
: 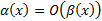 при
при 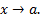
4. Если  , то
, то  – бесконечно малая низшего порядка малости при
– бесконечно малая низшего порядка малости при  по сравнению с
по сравнению с 
5. Если  ,
,  то
то  называется бесконечно малой порядка k по сравнению с
называется бесконечно малой порядка k по сравнению с 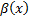 при
при 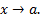
Эквивалентные бесконечно малые функции.
Если  , то бесконечно малые функции
, то бесконечно малые функции  и
и 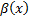 называются эквивалентными или равносильными бесконечно малой одного порядка при
называются эквивалентными или равносильными бесконечно малой одного порядка при 
 .
.
Теоремы об эквивалентных бесконечно малых функциях:
1. Для того, чтобы две бесконечно малые функции  и
и 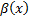 были эквивалентны необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка малости, чем каждая из них:
были эквивалентны необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка малости, чем каждая из них: 
2. Предел отношения двух бесконечно малых не изменяется, если любую из них заменить эквивалентной ей бесконечно малой.
Дано: 

Доказать: 
Доказательство.




Приращение аргумента и приращение функции, их геометрическая иллюстрация. Два равносильных определения функции.
 – приращение (изменение) независимой переменной.
– приращение (изменение) независимой переменной.
 – приращение функции в точке
– приращение функции в точке  , соответствует приращению
, соответствует приращению  .
.
Функция 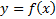 называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента
, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 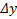 .
.
 (
(  )
)
Функция 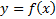 называется непрерывной в точке
называется непрерывной в точке  , если существует предел
, если существует предел  и этот предел равен значению
и этот предел равен значению  функции в точке
функции в точке  .
.


|

|

|

|
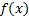
|
| y |
| x |

|

|
| y=f(x) |
Каждая элементарная функция непрерывна в каждой точке, где она определена.







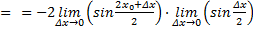

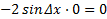
Определение непрерывности функции в точке.
I.

|
 определена в т. определена в т. 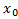
|
| |

|
| y=f(x) |

|
| x |
| y |
 называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке некоторой ее окрестности, существует предел функции
, если она определена в этой точке некоторой ее окрестности, существует предел функции 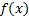 при
при  и это предел равен значению функции в точке
и это предел равен значению функции в точке  .
.
II.
| y |

|
| x |
| |

|

|
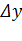
|

|
 (
(  ) )
|
 называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента
, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 
Теорема о непрерывности, произведения частного функций в точке (формулировка, доказательство).
Теорема.
Сумма, произведение и частное двух непрерывных функций – непрерывны.
Доказательство:
Пусть  . Тогда, по теореме о пределе произведения:
. Тогда, по теореме о пределе произведения:

Теорема:
Пусть функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  . Тогда сложная функция
. Тогда сложная функция  , состоящая их непрерывных функций, непрерывна в точке
, состоящая их непрерывных функций, непрерывна в точке  .
.
Доказательство:
Так как  – непрерывна, то
– непрерывна, то  , то есть при
, то есть при  имеем
имеем  . Поэтому (так как
. Поэтому (так как  – непрерывна) имеем:
– непрерывна) имеем:

9. Определение производной. Определение касательной и нормали к кривой. Геометрический смысл производной. Уравнения касательной и нормали к графику 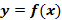 в данной точке (с обоснованием).
в данной точке (с обоснованием).

|
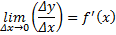
|
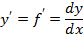
|
 функции
функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю.
называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю.
Таким образом, по определению

Касательная к графику функции  в некоторой его точке
в некоторой его точке  , для которой
, для которой  , есть прямая, проходящая через эту точку и имеющая угловой коэффициент
, есть прямая, проходящая через эту точку и имеющая угловой коэффициент  кас, равный
кас, равный  .
.

Нормалью к кривой называется прямая, проходящая через эту точку касания перпендикулярно касательной.

 кас
кас 

 н
н 



| с |
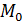
|
| нормаль |
| касательная |

|

|

|

|
 н н  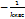 
|

|
Геометрический смысл производной
Значение производной в точке  равно угловому коэффициенту касательной, проведенной к графику функции в этой точке.
равно угловому коэффициенту касательной, проведенной к графику функции в этой точке.

|

|

|

|

|
10. Таблица производных элементарных функций. Вывод производных для  ,
,  ,
, 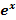 ,
,  .
.

Теорема 1. Производная синуса равна косинусу:
 Доказательство. Пусть аргумент х получил приращение
Доказательство. Пусть аргумент х получил приращение  . Тогда функция . Тогда функция  получит приращение получит приращение
 Воспользовавшись первым замечательным пределом и свойствами предела функции, получаем
Воспользовавшись первым замечательным пределом и свойствами предела функции, получаем
 Теорема доказана.
Теорема доказана.
|
Теорема 2. Производная тангенса:
 Доказательство.
Доказательство.
 Теорема доказана
Теорема доказана
|
Теорема 3. Производная 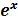 :
:

Доказательство. Найдем сначала приращение функции  в точке
в точке  :
:
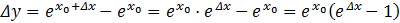
Находим:

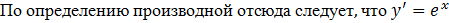 т. е.
т. е.  при любом
при любом  .
.
Теорема доказана
Теорема 4. Производная  :
:

Доказательство.


Теорема доказана
|
из
5.00
|
Обсуждение в статье: Теорема о непрерывности, произведения частного функций в точке (формулировка, доказательство). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

