 |
Главная |
Глава I Основные положения математической физики и теории дифференциальных уравнений
|
из
5.00
|
Собственные колебания пластин
Выполнила:
студентка V курса математического факультета
Чураева Анна Сергеевна
Научный руководитель: старший преподаватель кафедры математического анализа и МПМ С.А. Фалелеева
Рецензент: старший преподаватель кафедры математического анализа и МПМ Л.В. Ончукова
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой М.В. Крутихина
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение........................................................................................................... 3
Глава I Основные положения математической физики и теории дифференциальных уравнений.................................................................................................... 4
1.1 Поперечные колебания. Начальные и граничные условия..................... 4
1.2 Метод разделения переменных или метод Фурье................................... 6
1.3 Однородные линейные уравнения второго порядка с постоянными коэффициентами......................................................................................... 8
Глава II Нахождение функций, описывающих собственные колебания мембран 11
2.1 Основные определения............................................................................ 11
2.2 Собственные колебания прямоугольной мембраны.............................. 12
2.3 Собственные колебания круглой мембраны.......................................... 19
Заключение.................................................................................................... 28
Библиографический список........................................................................... 29
Приложение................................................................................................... 30
Введение
Математическая физика ставит своей задачей возможно более точное изучение явлений природы. С этой целью она использует аппарат математики. Объектом изучения математической физики могут служить только те явления природы, которые поддаются измерению. Например, механическое движение, звук, теплота, свет и т. д.
Цели работы:
Изучить математическую литературу по данной теме.
2. Освоить основные методы решения задач математической физики и применить их к решению задач.
Задачи работы:
1. Решить двумерное уравнение колебаний мембраны при дополнительных условиях для прямоугольной и круглой мембраны.
2. Сравнить полученные результаты для обоих случаев с аналогичными задачами, решенными для других дополнительных условий.
Методы работы:
· Изучение специальной литературы;
· Решение задач.
Глава I Основные положения математической физики и теории дифференциальных уравнений
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т. д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Дифференциальным уравнением с частными производными называется равенство, содержащее неизвестную функцию от нескольких переменных, независимые переменные и частные производные неизвестной функции по независимым переменным. Решением уравнения с частными производными называется функция, обращающая это уравнение в тождество [4].
1.1 Поперечные колебания. Начальные и граничные условия
При математическом описании физического процесса нужно, прежде всего, поставить задачу, т.е. сформировать условия, достаточные для однозначного определения процесса. Дифференциальные уравнения с частными производными имеют, вообще говоря, бесконечное множество решений. Поэтому в том случае, когда физическая задача приводится к уравнению с частными производными, для однозначной характеристики процесса необходимо задать некоторые дополнительные условия.
В случае обыкновенного дифференциального уравнения 2-го порядка частное решение определяется начальными условиями, например, заданием значений функции и ее первой производной при «начальном» значении аргумента. Для уравнения с частными производными возможны различные формы дополнительных условий.
 Рассмотрим их для задачи о поперечных колебаниях струны (под струной понимаем тонкую упругую нить). Каждую точку струны длины l можно охарактеризовать значением ее абсциссы x. Для определения положения струны в момент времени t достаточно задать компоненты вектора смещения точки x в момент t . Тогда
Рассмотрим их для задачи о поперечных колебаниях струны (под струной понимаем тонкую упругую нить). Каждую точку струны длины l можно охарактеризовать значением ее абсциссы x. Для определения положения струны в момент времени t достаточно задать компоненты вектора смещения точки x в момент t . Тогда 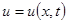 будет задавать отклонение струны от оси абсцисс.
будет задавать отклонение струны от оси абсцисс.
|
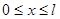 закреплены, то должны выполняться граничные условия
закреплены, то должны выполняться граничные условия
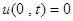 ,
, 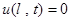 .
.
Так как процесс колебания струны зависит от ее начальной формы и распределения скоростей, то следует задать начальные условия:
|
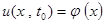 ,
,
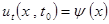 .
.
Таким образом, дополнительные условия состоят из граничных и начальных условий, где 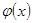 и
и 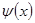 – заданные функции точки.
– заданные функции точки.
|
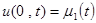 ,
, 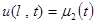 ,
,
где 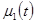 и
и 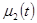 - заданные функции времени t.
- заданные функции времени t.
Возможны и другие типы граничных условий. Рассмотрим, например, задачу о продольных колебаниях пружины, один конец которой закреплен (точка подвеса), а другой конец свободен. Закон движения свободного конца не задан и зачастую является искомой функцией.
В точке подвеса x =0 отклонение
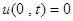 ;
;
на свободном конце x = l натяжение пружины
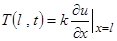
равно нулю (нет внешних сил), так что математическая формулировка условия свободного конца имеет вид
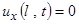 .
.
Если конец x =0 движется по определенному закону 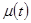 , а при x = l задана сила
, а при x = l задана сила 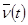 , то
, то
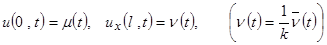 .
.
Типичным является также условие упругого закрепления, скажем для x = l
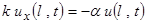 или
или 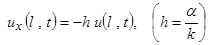 ,
,
при котором конец x = l может перемещаться, но упругая сила закрепления вызывает на этом конце натяжение, стремящееся вернуть сместившийся конец в прежнее положение.
Если точка (система), относительно которой имеет место упругое закрепление, перемещается, и ее отклонение от начального положения задается функцией 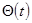 , то граничное условие принимает вид
, то граничное условие принимает вид
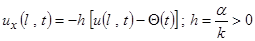 .
.
Условие упругого закрепления при x =0 имеет вид
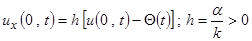 .
.
Таким образом, имеют место три основных типа граничных условий, например, при x =0:
§ граничные условия 1-го рода 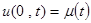 - заданный режим,
- заданный режим,
§ граничное условие 2-го рода 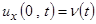 - заданная сила,
- заданная сила,
§ граничное условие 3-го рода 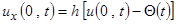 - упругое закрепление.
- упругое закрепление.
Аналогично задаются граничные условия и на втором конце x = l . Если функция, задаваемая в правой части ( 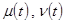 или
или 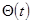 ), равны нулю, то граничные условия называются однородными [8].
), равны нулю, то граничные условия называются однородными [8].
1.2 Метод разделения переменных или метод Фурье
Одним из наиболее распространенных методов решения уравнений с частными производными является метод разделения переменных или метод Фурье.
Пусть требуется найти функцию 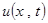 , удовлетворяющую для t >0 уравнению
, удовлетворяющую для t >0 уравнению
|
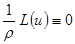
в области D и дополнительным начальным и граничным условиям, где 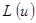 дифференциальное уравнение с частными производными второго порядка.
дифференциальное уравнение с частными производными второго порядка.
Попытаемся с помощью суперпозиции всех линейно независимых частных решений описанного типа (т. е. удовлетворяющих граничному условию) удовлетворить и начальным условиям. Для этого будем искать нетривиальные частные решения уравнения (1.2.1), удовлетворяющие граничным условиям, в классе функций вида 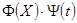 (где
(где 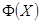 непрерывны в
непрерывны в 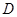 ,
, 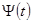 непрерывны в
непрерывны в 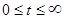 ). Подставляя функцию
). Подставляя функцию 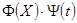 в уравнение (1.2.1) и деля обе части уравнения на
в уравнение (1.2.1) и деля обе части уравнения на 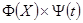 , получаем
, получаем
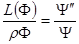 .
.
Чтобы это равенство было тождественно (т.е. чтобы функция 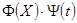 удовлетворяла уравнению (1.2.1) при всех
удовлетворяла уравнению (1.2.1) при всех 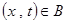 ) необходимо и достаточно, чтобы обе дроби были равны одной и той же константе
) необходимо и достаточно, чтобы обе дроби были равны одной и той же константе
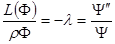 .
.
|
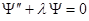 ,
,
|
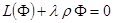 ,
,
причем функция 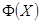 должна удовлетворять граничным условиям. Соответствующая краевая задача для уравнения (1.2.3) имеет нетривиальные решения не при всех значениях
должна удовлетворять граничным условиям. Соответствующая краевая задача для уравнения (1.2.3) имеет нетривиальные решения не при всех значениях 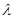 . Те значения
. Те значения 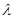 , при которых она будет иметь нетривиальные решения, называются собственными значениями краевой задачи, а соответствующие им решения
, при которых она будет иметь нетривиальные решения, называются собственными значениями краевой задачи, а соответствующие им решения 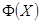 уравнения (1.2.3) – собственными функциями краевой задачи.
уравнения (1.2.3) – собственными функциями краевой задачи.
Суть метода Фурье:
ищем решение уравнения (1.2.1), удовлетворяющее только граничным условиям, среди функций вида 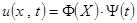 . Для функции
. Для функции 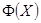 получаем краевую задачу;
получаем краевую задачу;
решаем краевую задачу для функции 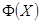 . Пусть
. Пусть 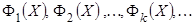 суть собственные функции этой задачи, а
суть собственные функции этой задачи, а 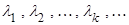 - отвечающие им собственные значения;
- отвечающие им собственные значения;
для каждого собственного значения 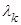 находим решение уравнения (1.2.3);
находим решение уравнения (1.2.3);
таким образом, частным решением уравнения (1.2.1), удовлетворяющим только граничному условию, являются функции вида 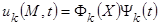 ;
;
возьмем сумму таких частных решений по всем собственным функциям 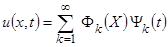 .Данная функция будет являться общим решением рассматриваемой задачи. Причем коэффициенты выбираются таким образом, чтобы эти суммы были решениями начальной задачи [2].
.Данная функция будет являться общим решением рассматриваемой задачи. Причем коэффициенты выбираются таким образом, чтобы эти суммы были решениями начальной задачи [2].
1.3 Однородные линейные уравнения второго порядка с постоянными коэффициентами
При решении задач математической физики часто приходят к линейным дифференциальным уравнениям второго порядка. Уравнение
|
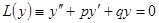
является однородным линейным уравнением второго порядка с коэффициентом при старшей производной равным единице, а 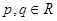 . Рассмотрим решение уравнения (1.3.1), оно может быть сведено к алгебраическим операциям и получено в элементарных функциях.
. Рассмотрим решение уравнения (1.3.1), оно может быть сведено к алгебраическим операциям и получено в элементарных функциях.
В силу общих свойств линейного уравнения, нам достаточно найти два частных решения, образующих фундаментальную систему решений.
Покажем, что выражение
|
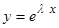 ,
,
где 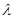 – действительное число, будет удовлетворять нашему уравнению.
– действительное число, будет удовлетворять нашему уравнению.
Продифференцируем по x выражение (1.3.2):
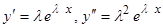 .
.
Подставляем полученные выражения в (1.3.1):
|
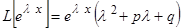 .
.
Обозначим через 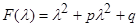 - это есть характеристический многочлен, соответствующий оператору L. Тогда (1.3.3) запишется в виде
- это есть характеристический многочлен, соответствующий оператору L. Тогда (1.3.3) запишется в виде 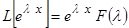 .
.
Характеристический многочлен получается из оператора L [ y ], если производные различных порядков в этом уравнении заменить равными степенями величины 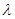 :
: 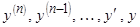 на
на 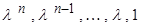 .
.
|
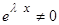 , следовательно
, следовательно
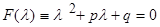 .
.
Уравнение (1.3.4) – есть алгебраическое уравнение с неизвестным 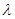 , оно называется характеристическим уравнением. Если мы в качестве постоянной
, оно называется характеристическим уравнением. Если мы в качестве постоянной 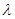 в выражение
в выражение 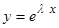 возьмем корень
возьмем корень 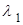 характеристического уравнения (1.3.4), то
характеристического уравнения (1.3.4), то 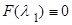 , т.е.
, т.е. 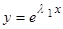 будет решением дифференциального уравнения (1.3.1).
будет решением дифференциального уравнения (1.3.1).
Уравнение (1.3.4) – уравнение 2-ой степени, следовательно, имеет 2 корня. Если все корни различны, то каждый из них соответствует частному решению дифференциального уравнения (1.3.1).
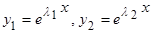
Следовательно, общее решение уравнения (1.3.1) будет
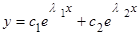 ,
,
где 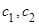 - произвольные постоянные, а
- произвольные постоянные, а 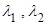 - решения характеристического уравнения (1.3.4) [6].
- решения характеристического уравнения (1.3.4) [6].
|
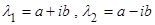 , то они будут сопряженными, т.к. коэффициенты уравнения действительные числа. В таком случае, общим решением уравнения (1.3.5) будет
, то они будут сопряженными, т.к. коэффициенты уравнения действительные числа. В таком случае, общим решением уравнения (1.3.5) будет
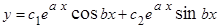 .
.
Если корни характеристического уравнения чисто мнимые, т.е. 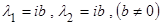 . Общим решением уравнения (1.3.1) будет
. Общим решением уравнения (1.3.1) будет
|
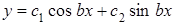 .
.
Если предположить, что характеристическое уравнение имеет равные корни 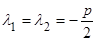 , то одно частное решение будет иметь вид
, то одно частное решение будет иметь вид
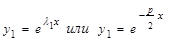 .
.
Второе частное решение будет
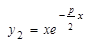 .
.
Тогда общее решение уравнения (1.3.1) можно представить в виде
|
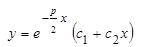 .
.
Глава II Нахождение функции, описывающей собственные колебания мембраны
2.1 Основные определения
В этой главе использованы следующие обозначения
· 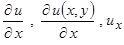 - частная производная функции
- частная производная функции 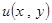 по
по 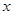 ;
;
· 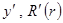 - производная функция одной переменной.
- производная функция одной переменной.
Мембраной называется плоская пластинка, не сопротивляющаяся изгибу и сдвигу. Мы будем рассматривать поперечные колебания мембраны, в которых смещение перпендикулярно к плоскости мембраны. Отклонение точек мембраны от плоскости xOy будем обозначать через функцию 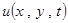 , которая зависит от координат точки ( x , y ) и от времени t. Вывод дифференциальных уравнений задач математической физики сопровождается целым рядом допущений как механических, так и геометрических. Так при выводе уравнения колебания прямоугольной мембраны мы пренебрегли квадратом частных производных
, которая зависит от координат точки ( x , y ) и от времени t. Вывод дифференциальных уравнений задач математической физики сопровождается целым рядом допущений как механических, так и геометрических. Так при выводе уравнения колебания прямоугольной мембраны мы пренебрегли квадратом частных производных
|
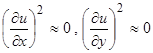 .
.
В результате получается следующее уравнение колебаний прямоугольной мембраны
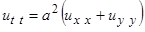 .
.
В случае рассмотрения мембраны круглой формы полезно перейти к полярным координатам. Пусть мембрана в состоянии покоя занимает круг радиуса 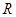 с центром в начале координат. Введем полярные координаты
с центром в начале координат. Введем полярные координаты 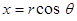 ,
, 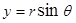 . Уравнение границы круга будет при этом
. Уравнение границы круга будет при этом 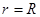 . Отклонение точек мембраны является теперь функцией полярных координат
. Отклонение точек мембраны является теперь функцией полярных координат 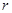 и
и 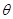 и времени t:
и времени t:
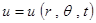 .
.
Выражение для оператора 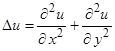 в полярных координатах имеет вид
в полярных координатах имеет вид
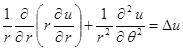 ,
,
Тогда уравнение колебаний мембраны (2.1.1) перепишется в виде
|
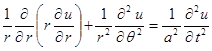 .
.
В данной главе нам еще понадобится определение ортогональных функций в следующем виде:
Система функций 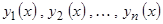 называется ортогональной на интервале
называется ортогональной на интервале 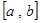 , если интеграл от произведения любых двух различных функций системы равен нолю:
, если интеграл от произведения любых двух различных функций системы равен нолю: 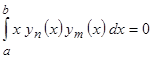 (
( 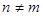 ). Это условие ортогональности отличается от обычного тем, что под интегралом содержится множитель
). Это условие ортогональности отличается от обычного тем, что под интегралом содержится множитель 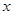 , в таких случаях говорят об ортогональности с весом
, в таких случаях говорят об ортогональности с весом 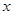 [1].
[1].
2.2 Собственные колебания прямоугольной мембраны
Процесс колебания плоской однородной мембраны описывается уравнением
|
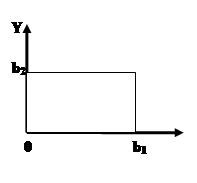
|
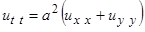
Пусть в плоскости ( x , y ) расположена прямоугольная мембрана со сторонами b1 и b2, закрепленная по краям. Ее колебание вызывается с помощью начального отклонения и начальной скорости.
Для нахождения функции 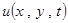 , характеризующей отклонение мембраны от положения равновесия (прогиб), нужно решить уравнение колебаний при заданных начальных условиях
, характеризующей отклонение мембраны от положения равновесия (прогиб), нужно решить уравнение колебаний при заданных начальных условиях
|
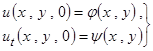
и граничных условиях
|
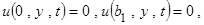
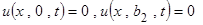 .
.
Краткое решение задачи (2.2.1) – (2.2.3) приведено в книге [8], где были получены следующие результаты.
Функция 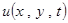 имеет вид
имеет вид
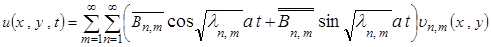 ,
,
где 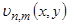 - собственные функции, соответствующие собственным значениям
- собственные функции, соответствующие собственным значениям 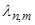 (полученным в результате применения метода Фурье) и определяющиеся формулой
(полученным в результате применения метода Фурье) и определяющиеся формулой
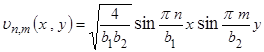 .
.
А коэффициенты 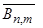 и
и 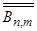 равны:
равны:
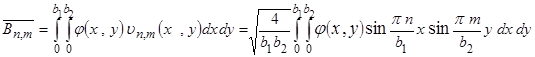 ,
,
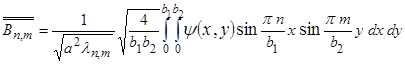 .
.
Найдем решение задачи при других граничных условиях.
Итак, для нахождения функции 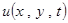 , характеризующей прогиб мембраны мы должны решить уравнение колебаний мембраны (2.2.1) при заданных начальных условиях
, характеризующей прогиб мембраны мы должны решить уравнение колебаний мембраны (2.2.1) при заданных начальных условиях
|
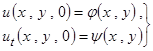
и граничных условиях
|
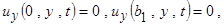
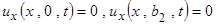 .
.
|
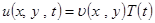
|
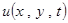 в уравнение (2.2.1) и, поделив обе части уравнения на
в уравнение (2.2.1) и, поделив обе части уравнения на 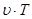 (при этом мы не теряем решений, т. к.
(при этом мы не теряем решений, т. к. 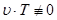 ), получаем
), получаем
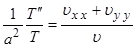 .
.
Чтобы функция (2.2.6) была решением уравнения (2.2.1), равенство (2.2.7) должно удовлетворяться тождественно, т.е. для любых значений переменных 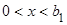 ,
, 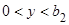 ,
, 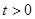 . Правая часть равенства (2.2.7) является функцией только переменных ( x , y ), а левая – только t. Фиксируя, например, некоторые значения x и y и меняя t (или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно
. Правая часть равенства (2.2.7) является функцией только переменных ( x , y ), а левая – только t. Фиксируя, например, некоторые значения x и y и меняя t (или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно 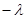 .
.
|
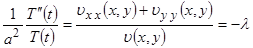 ,
,
где 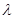 - постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
- постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
|
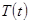 :
:
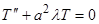 ,
,
а для функции 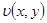 следующую краевую задачу:
следующую краевую задачу:
|
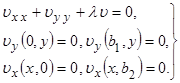
Таким образом, сама задача о собственных значениях состоит в решении однородного уравнения в частных производных при заданных граничных условиях. Снова применим метод разделения переменных. Пусть
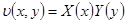
|
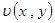 в уравнение
в уравнение 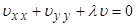 и, поделив обе части уравнения на
и, поделив обе части уравнения на 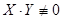 , приведем его к виду
, приведем его к виду
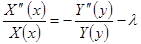 .
.
Правая часть равенства (2.2.10) является функцией только переменной y, а левая – только x. Фиксируя, например, некоторые значения x и меняя 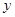 (или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно
(или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно 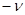 .
.
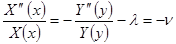
Тогда из данного соотношения получаем два однородных дифференциальных уравнения второго порядка:
1. 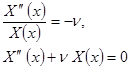
2. 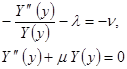
где 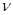 и
и 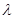 - постоянные разделения переменных, причем
- постоянные разделения переменных, причем 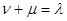 . При этом граничные условия для
. При этом граничные условия для 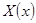 и
и 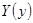 вытекают из соответствующих условий для функции
вытекают из соответствующих условий для функции 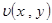 .
.
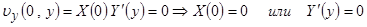 ,
,
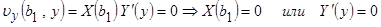 ,
,
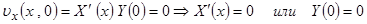 ,
,
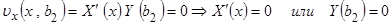 .
.
Получаем следующие одномерные задачи на собственные значения:
(2.2.11) 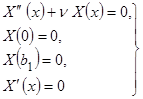
(2.2.12) 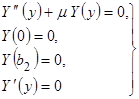
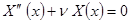 - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Таким образом, общее решение данного уравнения зависит от параметра
- линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Таким образом, общее решение данного уравнения зависит от параметра 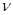 . Рассмотрим отдельно случаи, когда параметра
. Рассмотрим отдельно случаи, когда параметра 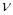 отрицателен, равен нулю, положителен.
отрицателен, равен нулю, положителен.
1) При 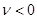 задача не имеет нетривиальных решений. Общее решение уравнения
задача не имеет нетривиальных решений. Общее решение уравнения 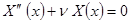 имеет вид
имеет вид
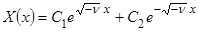 ,
,
т. к. характеристическое уравнение 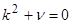 имеет корни
имеет корни 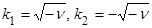 .
.
Учитывая граничные условия, получаем:
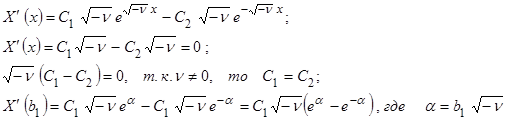
т.к. 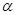 - действительно и положительно, то
- действительно и положительно, то 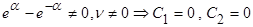 .
.
2) При 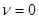 нетривиальных решений тоже не существует.
нетривиальных решений тоже не существует.
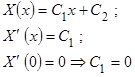
3) При 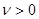 общее решение уравнения
общее решение уравнения 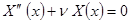 имеет вид
имеет вид
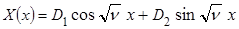 .
.
Учитывая граничные условия, получаем:
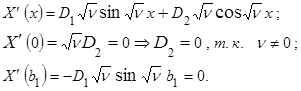
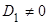 , т.к. мы ищем нетривиальные решения,
, т.к. мы ищем нетривиальные решения, 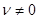 , следовательно
, следовательно
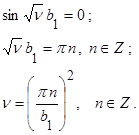
Итак, только при значениях равных 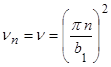 , существуют нетривиальные решения задачи (2.2.11) и имеют вид
, существуют нетривиальные решения задачи (2.2.11) и имеют вид
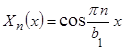 .
.
Они определяются с точностью до произвольного сомножителя, который мы положили равным единице.
Аналогично получаем решение задачи (2.2.12):
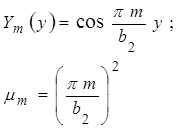
Собственным значениям 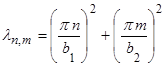 , таким образом, соответствуют собственные функции
, таким образом, соответствуют собственные функции
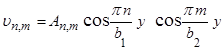 ,
,
где 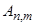 - некоторый постоянный множитель. Выберем его так, чтобы норма функций
- некоторый постоянный множитель. Выберем его так, чтобы норма функций 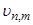 с весом единица была равна единице
с весом единица была равна единице
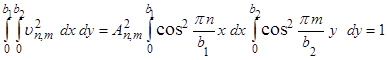 .
.
Вычислим отдельно интегралы в равенстве:
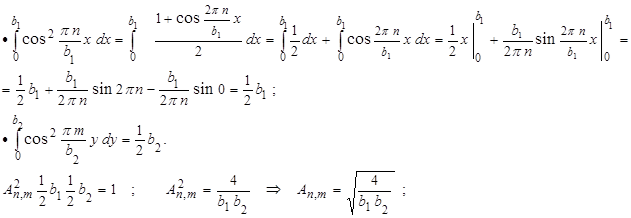
|
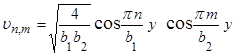 .
.
Число собственных функций, принадлежащих 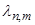 зависит от количества целочисленных решений n и m уравнения
зависит от количества целочисленных решений n и m уравнения
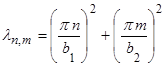 .
.
Собственным значениям 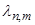 соответствуют решения уравнения
соответствуют решения уравнения 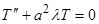 :
:
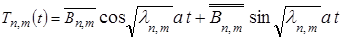 ,
,
где 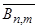 и
и 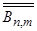 - произвольные константы.
- произвольные константы.
Возвращаясь к начальной задаче для уравнения 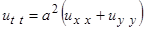 с дополнительными условиями (2.2.4) – (2.2.5), получаем, что частные решения будут иметь вид
с дополнительными условиями (2.2.4) – (2.2.5), получаем, что частные решения будут иметь вид
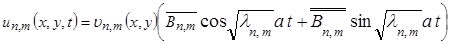 .
.
Тогда общее решение запишется в виде
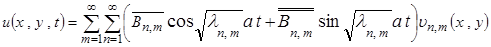 ,
,
где 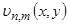 определяется формулой (2.2.13), а коэффициенты
определяется формулой (2.2.13), а коэффициенты 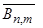 и
и 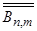 равны:
равны:
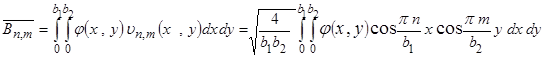 ,
,
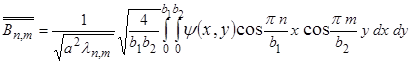 .
.
В задачах, рассмотренных в этом параграфе, необходимо было найти функцию, описывающую отклонение мембраны от положения равновесия при одинаковых начальных условиях, но при различных граничных условиях. В результате были получены две разные функции. Таким образом, можно сказать, что прогиб мембраны напрямую зависит от граничных условий.
2.3 Собственные колебания круглой мембраны
Сравним теперь результаты решения двух задач о нахождении функции, характеризующей прогиб мембраны, также при заданных различных граничных условиях, одинаковых начальных условиях, но уже для круглой мембраны.
|
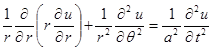 .
.
Будем искать решение этого уравнения при заданных начальных условиях
|
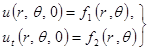
|
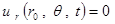 .
.
Применим метод разделения переменных. Пусть
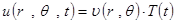 .
.
Подставляем полученное выражение для функции 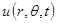 в уравнение (2.3.1), получаем:
в уравнение (2.3.1), получаем:
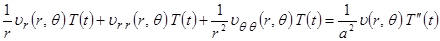 .
.
|
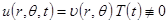 , полученное равенство можно поделить на
, полученное равенство можно поделить на 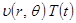 . Тогда
. Тогда
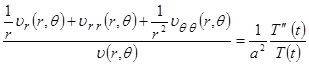 .
.
Из соотношения (2.3.4) получаем однородное дифференциальное уравнение второго порядка для функции 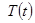
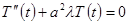 ,
,
|
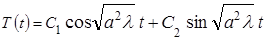 ,
,
и следующую задачу на собственные значения для функции 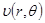 :
:
|
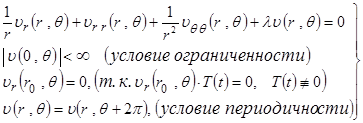
К задаче (2.3.6) снова применим метод Фурье для нахождения функции 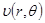 . Пусть
. Пусть 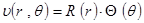 , подставляем в уравнение для функции
, подставляем в уравнение для функции 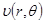 .
.
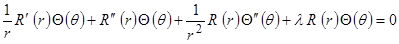
Поделим данное равенство на 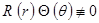 :
:
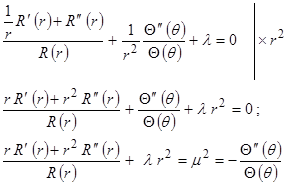
Так как левая часть соотношения ( 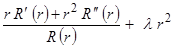 ) функция только переменной r, а правая (
) функция только переменной r, а правая ( 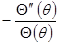 ) - только переменной
) - только переменной 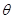 , то равенство должно сохранять постоянное значение, пусть оно равно
, то равенство должно сохранять постоянное значение, пусть оно равно 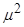 . При данном предположении получаем:
. При данном предположении получаем:
1) однородное дифференциальное уравнение второго порядка для нахождения функции 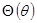 :
:
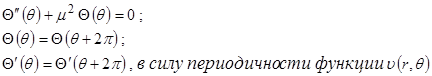
Нетривиальные периодические решения для 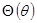 существуют лишь при
существуют лишь при 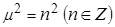 и имеют вид (см. 2.2):
и имеют вид (см. 2.2):
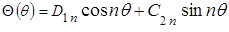 .
.
2) уравнение для определения функции 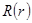
|
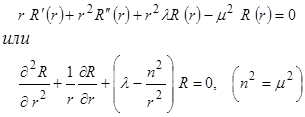
|
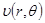 получаем граничные условия для функции
получаем граничные условия для функции 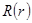 :
:
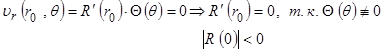
Таким образом, требуется решить задачу о собственных значениях.
Введем новую переменную


