Пример. Пусть имеется система линейных уравнений

 

 

Представим эту систему в матричном виде

 

 

Если ввести пространство матриц – столбцов R, то  где

 

 

и  Здесь оператор А – матрица размера n x n

 

 

Если матрица А невырождена, то обратная матрица и является обратным оператором:

 

Определение. Линейное пространство R называется метрическим, если каждой паре элементов х, y Î R ставится в соответствие вещественное число r (x, y) – расстояние между x и y – удовлетворяющее условиям:

 

1. r (x, y) ³ 0, если r (x, y) = 0, то x = y;

2. r (x, y) = r (y, x);

3. r (x, y) £ r (x, z) + r (z, y) (неравенство треугольника).

 

Если введением расстояния пространство R превращено в метрическое пространство, то говорят, что в пространстве R введена метрика.

В радиотехнике элементами пространства являются сигналы (токи или напряжения), математическими моделями которых являются функции времени x(t), y(t), ... . Рассмотрим следующее пространство сигналов.

1. С_{[a, b]} - пространство непрерывных на промежутке [a, b] функций с метрикой:

 

 y(t)

r(x,y)

 

2. L²_{(a, b)} - пространство интегрируемых в квадрате функций (x(t) Î L²_{(a, b)}, если  с метрикой

 

 

Определение. Элементы линейного пространства R называются линейно независимыми, если из условия

 

 

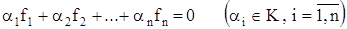
следует, что

 

a₁ = a₂ = . . . = a_n = 0.

 

В противном случае элементы f₁, f₂, . . . , f_n считаются линейно зависимыми.

Максимальное число линейно независимых элементов определяет размерность dim R пространства R и образуют базис этого пространства. Если m = dim R, то пространство обозначается R_m.

 

2. Линейные нормированные пространства

 

Определение. Линейное пространство R называется нормированным, если каждому элементу х Î R ставится в соответствие вещественное число  ("длина" элемента х), называемое нормой х, которое удовлетворяет условиям:

1. 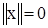, тогда х = 0;

2.  (однородность нормы);

3.  (неравенство треугольника).

Положив для

 

 

превращаем нормированное пространство R в метрическое.

Можно и метрическое пространство R превратить в нормированное, если метрика удовлетворяет условиям:

 

 положив

 

Рассмотренные ранее пространства сигналов С_[a,b] и L²_(a,b) становятся соответственно нормированными, если

 

и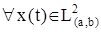

 

Если положить а = ¥, b = ¥, то квадрат этой нормы в теории сигналов носит название энергии сигнала.

 

так как такая энергия выделяется на резисторе с сопротивлением в 1 Ом при напряжении x(t) на его зажимах.

Пример. Имеется треугольный импульс длительности t:

 

 

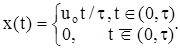
Вычислить энергию и норму сигнала.

Решение.

 

 

3. Линейное унитарное пространство

 

Определение. Линейное нормированное пространство R называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов x, y Î R ставит в соответствие действительное или комплексное число (x, y), удовлетворяющее условиям

 

1. (x, y) = (y, x)* ( _* - знак комплексного сопряжения);

2. (a₁ х₁ + a₂ х₂, y) = a₁(x₁, y) + a₂(x₂, y) (a₁, a₂ Î K);

3. (x, x) ³ 0, если (х, х) = 0, то х = 0.

 

В унитарном пространстве норма вводится следующим образом

 

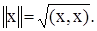
Теорема 1. Для " х, y унитарного пространства R справедливо неравенство Шварца

 

 

Равенство имеет место лишь для линейно зависимых элементов.

Теорема 2. Для " х, y унитарного пространства R имеет место неравенство

 

 

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).

Теорема 3. Для " х, y унитарного пространства R выполняется равенство параллелограмма

 

 

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).

Определение. Два элемента х, y Î R (x ¹ 0, y ¹ 0) называются ортогональными, если (х, y) = 0.

Система элементов e₁, e₂, . . . , e_n, . . . унитарного пространства R называется ортонормированной, если

 

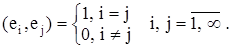
Пусть система элементов х₁, х₂, . . . , х_n, . . . ортогональна ((x_i, x_j)=0, i ¹ j), тогда ее можно нормировать, положив

 

 

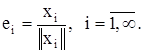
Из ортонормированности системы следует ее линейная независимость. Обратно – любую линейно независимую систему можно ортонормировать. Процесс ортонормированности следующий. Если система элементов y₁, y₂, . . . , y_n, . . . –линейно независимая, то система e₁, e₂, . . . , e_n, . . ., где

 

 

становится ортонормированной.

Пусть теперь f – любой элемент унитарного пространства R, a e₁, e₂, ..., e_n,... – ортонормированная система этого пространства. Величина

 

 

носит название коэффициента Фурье, а ряд

 

 

носит название ряда Фурье. Ряд Фурье наилучшим образом аппроксимирует f (приближается к f). Это значит, если рассматривать норму разности элемента f и ряда Фурье

 

то наименьшее значение норма примет при