Перевод чисел из троичной симметричной системы в десятичную

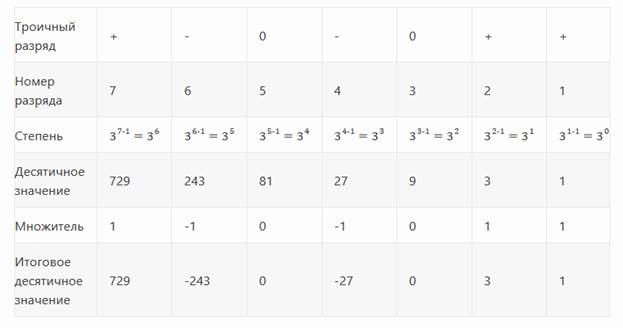
В общем виде число в троичной системе можно представить как сумму произведений значения разряда на соответствующую этому разряду степень числа 3.

Иными словами, вещественное число X можно записать в виде:

здесь .

Рассмотрим троичное число +-0-0++.

Подробнее

Перевод целых чисел из десятичной системы в троичную симметричную (уравновешенную) систему

Для перевода из десятичной системы в троичную уравновешенную с/с, можно воспользоваться следующим алгоритмом:

1. Исходное число (в десятичной системе) делим на 3.

2. Если остаток от деления равен 2, то к результату добавляем +1.

3. Если результат от деления больше 2, выполняем его деление на 3.

4. Пункты 2, 3 выполняем до тех пор, пока не получим результат от деления меньше 3 (см. п.3).

5. После выполнения процедур сначала выписываем результат от последнего деления, при этом если результат равен двум то его выписываем как +-, затем выписываем остатки от предыдущих операций, так что первый остаток от деления был выписан последним (то есть выписываем снизу вверх), при этом все остатки равные двум выписываются как значение - (см. п.2, мы делали заём из остатка в результат).

6. Значения равные 1 выписываются как +, 0 оставляем как есть (0 и в троичной системе 0).

Пример 1. Перевести число 155 в троичную уравновешенную с/с.

Перевод вещественных чисел

Рассматриваемый ниже способ перевода в троичную уравновешенную систему предложен известным программистом Дональдом Кнутом. Его суть заключается в следующем. Сначала записываем произвольное число в обычной троичной системе счисления (A).

Очевидно, что если к этому числу A добавить другое число B и затем его же вычесть, то в результате получится то же самое число A. Возьмем в качестве B бесконечное число, состоящее из одних единиц
. Теперь вычтем из суммы число B, причем

2-1=+1(+),

1-1=0,

0-1=-1(-).

Рассмотрим два несложных примера

Пример 2. Перевести число 0.57 в троичную уравновешенную с/с.

Пример 3. Перевести число 26 .57 в троичную уравновешенную с/с.

Отрицательные числа

Ключевая особенность троичной системы — наличие знака числа в самом алфавите, т.е. однозначно определяется знак числа по самому числу. Если ведущий ненулевой разряд отрицателен, то и само число является отрицательным. Изменение знака числа производится инвертированием каждого разряда числа: положительный разряд меняется на отрицательный и наоборот, ноль остается без изменений.

Округление

Другой важной особенностью троичной системы является механизм округления чисел — простым отбрасыванием младших разрядов получается наилучшее при данном оставшемся количестве цифр приближение этого числа и округление не требуется. Это следствие того, что абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа ( 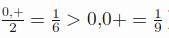), соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Округлим троичное число 0,++++=0,493827 до 3 знаков после запятой: 0,+++=0,48148 , до 2 знаков дает: 0,++=0,4444(4) , до 1 знака — 0,+=0,3333(3) .

Сложение

Сложение производится по общим правилам для позиционных систем.

Примечание: следует отметить, что разрядная сетка с двумя разрядами не переполняется вплоть до 4 слагаемых. Таким образом наименьшим оптимальным сумматором можно считать сумматор для четырёх одноразрядных операндов: «+» + «+» + «+» + «+» = «+-» + «+-» = «++»

Вычитание

Операция вычитание выполняется как сложение с инвертированием вычитаемого или уменьшаемого «+0-» - «-+» = «+0-» + «+-» = «+0+».

Умножение

Умножение производится по общим правилам для позиционных систем.

Умножение 8 (+0-) на 8 (+0-), в результате получаем 64.

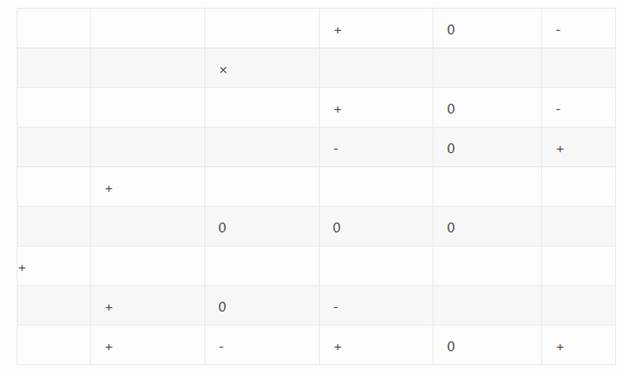
Примечание: умножение в троичной системы на  , где n>0, n∈N , сводится к добавлению к числу n – младших разрядов с нулевым значением: 4=++ ; 12=++0 ; 36=++00 , также эта операция называется троичный сдвиг влево.

Деление

Деление производится по общим правилам для позиционных систем. При делении столбиком, если разрядность остатка от деления не уменьшилось, необходимо произвести его деление без добавления следующего разряда делимого, а результат записать под предыдущем результатом, затем необходимо сложить полученные результаты поразрядно (можно заменять операцию вычитания – операцией сложения, для этого вычитаемое необходимо инвертировать, после чего можно производить сложение).

Пример: разделим 25 на 5.

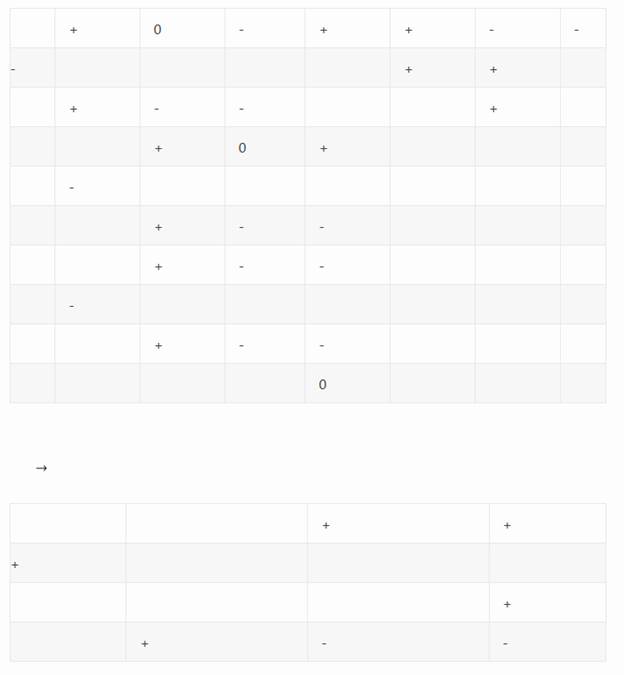
В результате второй операции вычитания получается остаток с разрядностью равной разрядности делителя, т.е. необходимо произвести деление остатка без займа следующего разряда делимого. Полученный результат записываем под предыдущим результатом.

Примечание: деление числа на , где n>0, n∈N, осуществляется сдвигом вправо: ;  ;  ; = +,-.