 |
Главная |
Шаг 2. Решается задача квадратической минимизации
|
из
5.00
|
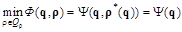 .
.
Шаг 3. На каждом итерационном шаге находится вектор направления убывания  функции
функции  .
.
 , (3.47)
, (3.47)
где малая величина 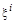 выбирается особым образом и зависит от линейного размера i-го ребра «гиперкуба».
выбирается особым образом и зависит от линейного размера i-го ребра «гиперкуба».
Находим точку  пересечения вектора
пересечения вектора  и границ данной ячейки оптимизации. На отрезке
и границ данной ячейки оптимизации. На отрезке  модифицированным методом «золотого сечения» производим поиск минимального значения функции
модифицированным методом «золотого сечения» производим поиск минимального значения функции  .
.
Шаг 4. Полученную точку принимаем за начальную 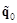 , и процесс повторяется с самого начала до тех пор, пока либо координаты точки совпадут с координатами, полученными на предыдущем этапе, и это будет решение, либо минимум окажется на границе, и мы переходим к следующей ячейке сетки.
, и процесс повторяется с самого начала до тех пор, пока либо координаты точки совпадут с координатами, полученными на предыдущем этапе, и это будет решение, либо минимум окажется на границе, и мы переходим к следующей ячейке сетки.
Таким способом удается достаточно точно выявить множество решений.

Рис. 3.2. Область локальной оптимизации
Этап 3. Проводится анализ полученного множества и на основе СТЭК выявляются равновесные решения, обладающие преимуществами по всем показателям.
Для СТЭК-3 этап 3 состоит из следующих шагов.
Шаг 1. Попарное сравнение всех решений и отбрасывание тех, чьи значения хуже по всем показателям (доминируемые точки).
Шаг 2. Формирование «идеальной точки»  (см. рис. 3.1)
(см. рис. 3.1)
 , (3.48)
, (3.48)
которая представляет собой вершину прямоугольной m-мерной пирамиды, образованной пересечением m плоскостей, перпендикулярных осям координат и проходящими через минимальные значения показателей (см. рис. 3.4).

Рис. 3.3. Формирование идеальной точки и проекций
Шаг 3. Выбор из прореженного множества решений  (доминирующих точек) точки, наиболее близкой к «идеальной», т.е. удовлетворяющей условию
(доминирующих точек) точки, наиболее близкой к «идеальной», т.е. удовлетворяющей условию
 . (3.49)
. (3.49)
Этап 4. Формирование проекции типа (рис 3.3б). Формирование оптимальных ПКЗУ ММС. Моделирование оптимальных траекторий ММС.
Блок-схема алгоритмической процедуры метода дана на рис. 3.4, 3.5.
Программное обеспечение алгоритма реализовано в рамках ПС MATLAB. Программы, программные модули даны в [45]. Применение данного подхода в задаче группового перехвата цели с учетом противодействия рассмотрено в [45] и в следующем пункте 3.4.
Повышение быстродействия алгоритма. В соответствии с рис. 3.5 для увеличения быстродействия алгоритма применены аппроксимация описания ММС, минимаксный подход для уменьшения области начальных условий и оценивается возможность параллельной реализации этапа 2 алгоритма (см. пункт 3.5).
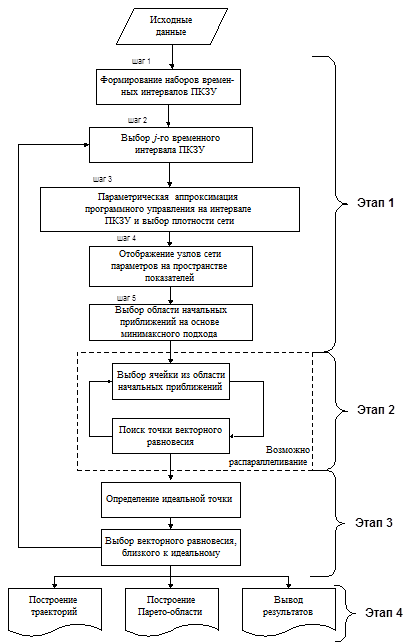
Рис. 3.4. Блок-схема алгоритма управления на основе векторного равновесия
с элементами анализа результатов

Рис. 3.5. Блок-схема алгоритма поиска векторного равновесия
с данным начальным приближением (этап 2)
3.4. Решение задачи коалиционного перехвата подвижной цели
с учетом противодействия на этапе ближнего наведения ЛА
3.4.1. Математическая модель ММС
С учетом приведенного выше формального описания модели ММС составим математическую модель перехвата высокоманевренными ЛА подвижной цели.
Динамическая модель ММС. Движение центров масс (ЦМ) ЛА описывается системой нелинейных дифференциальных уравнений в нормальной земной системе координат (СК) 0ДXДYДZД:
 (3.50)
(3.50)
где [XДi, YДi, ZДi], (i = 1…3) – координаты ЦМ ЛА; Vi – скорость ЛА;
Qi – угол наклона траектории полета ЛА; Yi – угол поворота траектории.
Далее будем предполагать, что каждый из ЛА движется без скольжения (bi = 0) и величины скоростей не меняются в течении всего времени взаимодействия коалиций (|Vi| = const).
Вектор состояния системы имеет вид:
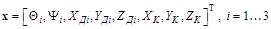 , (3.51)
, (3.51)
где XK, YK, ZK – координаты центра коалиции истребителей-перехватчиков (ИП):


В качестве вектора наблюдаемого выхода будем рассматривать расстояния между подсистемами ИП – цель и внутри коалиции ИП:
 , (3.55)
, (3.55)
где rj – расстояние между j-м ИП и целью:
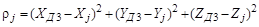 , (3.56)
, (3.56)
rK – расстояние от центра коалиции ИП до цели:
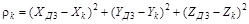 , (3.57)
, (3.57)
R – расстояние между ИП:
 . (3.58)
. (3.58)
Изменение положения ЛА в пространстве обеспечивается системой управления ЛА путем изменения величины перегрузки и ее направления (за счет «накренения» gi ЛА) (рис. 3.6). Поэтому вектор управления имеет вид
 , (3.59)
, (3.59)
где nyi = ni×cos(gi); nzi = ni×sin(gi).
| Вектор ограничений определяет конфигурацию истребителей-перехватчиков (ИП) внутри коалиции. Для звена – пары ЛА, находящегося в боевом порядке «фланг», система ИП представляет собой конфигурационно-пространственную линию, вписанную в шар или шаровой слой с центром в точке [XK, YK, ZK]. Для звена из трех ЛА данная точка – центр равностороннего треугольника. |  Рис. 3.6. Формирование вектора управления
Рис. 3.6. Формирование вектора управления
|
Ограничения, накладываемые на подсистему для поддержания данного боевого порядка, имеют вид:
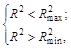 (3.60)
(3.60)
т.е. внутри коалиции ИП не могут удаляться друг от друга на расстояние более чем Rmax и сближаться менее Rmin.
Другими естественными ограничениями являются требования положительной высоты полета ЛА:
 . (3.61)
. (3.61)
Приведя ограничения (3.60) и (3.61) к стандартному виду, запишем вектор ga:
 (3.62)
(3.62)
Таким образом, полностью описана модель, характеризующая динамические особенности каждого из участников взаимодействия и всей системы в целом.
Векторный показатель и коалиционная структура системы естественно определяются из условия задачи. К первой коалиции относятся два истребителя-перехватчика. При этом она объединяет показатели: промах ИП относительно цели (его необходимо минимизировать) и энергетические затраты (их также необходимо минимизировать).
Поэтому вектор показателей первой коалиции:
 , (3.63)
, (3.63)
где lj – некоторые коэффициенты.
При помощи коэффициентов lj можно гибко менять смысл вектора интегральных показателей: при малых lj интегральные показатели в большей степени отслеживают промах, а не энергетические затраты, когда же lj>>1, на передний план выступает минимизация энергетических затрат при перехвате цели. Кроме этого, при l1¹l2 можно задать режим перехвата цели звеном с разделением функций ЛА «ведущий-ведомый» (l1 = l2 задают режим полета звена с равноправными ЛА). При разделении функций ЛА в звене основная задача по перехвату цели лежит на «ведущем», а «ведомый» выступает в качестве прикрытия «ведущего». Поэтому «ведущий» должен в большей степени учитывать промах при противодействии, чем «ведомый».
В интересах цели – уклониться от коалиции противника и удалиться от нее на максимально возможное расстояние при контролируемых энергетических затратах, поэтому
 . (3.64)
. (3.64)
Окончательно векторный показатель системы принимает вид
 (3.65)
(3.65)
ММС представляет собой две коалиции, векторный функционал которой не поддается скаляризации. Это связано, например, с тем, что тактические приемы коалиции ИП не только неизвестны заранее цели, но и могут меняться во время взаимодействия.
Формирование параметризованного ПКЗУ. Взаимодействие подсистем осуществляется на конечном интервале времени [t0,T]; t0 = 0 определяет момент начала взаимодействия подсистем, а Т – время окончания взаимодействия. Время Т определяется начальными условиями взаимодействия и параметрами управления, применяемыми каждой коалицией.
Разобьем интервал [t0,T] на n вложенных интервалов [tj-1,T]. Зададим на каждом интервале [tj-1,T] ПКЗУ программу управления в виде:
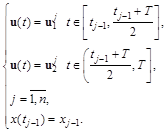 (3.66)
(3.66)
Как было показано в предыдущем параграфе, вектор управления однозначно определяется величиной нормальной перегрузки и углом крена ЛА. Поэтому запишем вектор оптимизируемых параметров в виде
 , (3.67)
, (3.67)
где  – вектор, заданный на интервале [tj-1,tП],
– вектор, заданный на интервале [tj-1,tП], 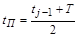 , j = 1…n;
, j = 1…n;
 – вектор, заданный на интервале
– вектор, заданный на интервале 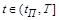 .
.
Выражение (3.66) примет вид:
 (3.68)
(3.68)
Поэтому задача выбора оптимальных параметров решается для области допустимых стратегий Q, состоящей из векторов вида (3.67) на интервале [tj-1,T],  .
.
Оптимальный вектор параметров q* в соответствии с (3.68) однозначно определяет оптимальный вектор управления u* = u(q*), который применяется на интервале [tj-1,tj]. После этого повторяется процедура поиска вектора оптимальных параметров для следующих интервалов. При этом начальные условия для вектора состояния динамической системы на всех последующих интервалах выбираются из условия:

где 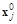 – начальные условия вектора состояния системы на интервале [tj,tj+1],
– начальные условия вектора состояния системы на интервале [tj,tj+1], 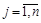 ;
;  – конечное значение вектора состояния системы на интервале [tj-1,tj],
– конечное значение вектора состояния системы на интервале [tj-1,tj], 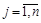 .
.
3.4.2. Анализ эффективности коалиционного перехвата
подвижной цели
Выбор плотности параметрической сети и точности определения векторного равновесия (ВР) для анализа эффективности ММС. При поиске ВР-точек на области параметров Q используется «сеть» размерности nq и густоты l (см. рис. 3.1).
Густота сети l неявно характеризует точность определения области показателей I в целом, а также Парето-множества и ВР-точек в частности. Помимо этого густота сети и размерность области Q напрямую связаны с интервалом времени оптимизации, поэтому уменьшение шага сети ведет к значительному увеличению времени поиска обобщенного равновесия, так как количество областей локальной оптимизации («ячеек сети») определяется из выражения
 , (3.69)
, (3.69)
где nq – размерность области параметров Q; li – густота сети по i-й координате; 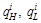 – верхняя и нижняя границы i-го компонента вектора параметров на области Q.
– верхняя и нижняя границы i-го компонента вектора параметров на области Q.

Рис. 3.7. Отображение сети пространства параметров на пространство показателей
На рис. 3.7 и рис. 3.8 даны допустимая область пространства показателей для разной плотности сети параметров на пространстве параметров Q.

Рис. 3.8. Отображение сети пространства параметров на пространство показателей
Таблица 3.1
Варианты «сетей» значений параметров
| Параметр | Диапазон изменения | Рис. 3.7 | Рис. 3.8 | |
| qL | qH | Количество интервалов | ||

| – 3 | 8 | 3 | 5 |
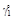
| – 60 | 60 | 1 | 1 |

| – 3 | 8 | 3 | 5 |

| – 60 | 60 | 1 | 1 |
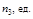
| – 1 | 5 | 2 | 3 |

| – 30 | 30 | 1 | 1 |
| Число «ячеек» в сети | 324 | 5625 | ||
Из рисунков видно, что более густая сеть точнее отображает всю область пространства показателей. Однако нас интересует не вся область, а только ее часть – Парето-множество и точки векторного Нэш-равновесия. А их с достаточной точностью можно определить и при менее густой сети, выиграв при этом во времени поиска решения. Так, оптимизация на сети из 324 «ячеек» выполняется в 17 раз быстрее, чем на сети из 5625 ячеек.
Анализ эффективности перехвата для догонных, поперечных и встречных курсов. В программной реализации алгоритма векторной Нэш-оптимизации (ВНО) рассматривается случай коалиционного перехвата цели (типа бомбардировщик F-111) двумя высокоманевренными летательными аппаратами (типа МиГ-21) в режиме ближнего наведения перехватчиков.
Расчет динамики конфликта проводился в [54] при следующих конфигурациях коалиций: перехват истребителями-перехватчиками цели «вдогон» (а), на поперечных (б) и встречных (в) курсах (рис. 3.9).

Рис. 3.9. Начальные конфигурации коалиций
Исходные данные и диапазоны изменения параметров для указанных конфигураций приведены в соответствующих таблицах (см. табл. 3.2, – табл. 3.4).
Таблица 3.2
Начальные условия
| Конфигурация | 
| 
| 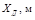
| 
| 
| |
| ИП1 | АБВ | 0 | 0 | 0 | 3200 | – 50 |
| ИП2 | АБВ | 0 | 0 | 0 | 3200 | 50 |
| Цель | А | 0 | 0 | 5000 | 2000 | 0 |
| Б | 0 | – 90 | 5000 | 2000 | 0 | |
| В | 0 | 180 | 5000 | 2000 | 0 |
Таблица 3.3
Значения параметров-констант
| № | Параметр | Значение |
| 1 | 
| 600 |
| 2 | 
| 600 |
| 3 | 
| 300 |
| 4 | 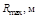
| 2000 |
| 5 | 
| 50 |
| 6 | 
| 1 |
| 7 | 
| 1 |
| 8 | 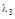
| 1 |
| 9 | 
| 9,8 |
Таблица 3.4
Диапазоны изменения оптимизируемых параметров
| № | Параметр | qL | qH |
| 1 | 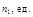
| – 3 | +8 |
| 2 | 
| – 3 | +8 |
| 3 | 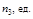
| – 1… – 3 | +5 |
Продолжение табл. 3.4
| 4 | 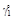
| – 60 | +60 |
| 5 | 
| – 60 | +60 |
| 6 | 
| – 30 | +30 |
Для всех исходных конфигураций коалиций были получены параметризованные программно-корректируемые законы управления для интервалов времени (где T определяется из условия сближения центра коалиции перехватчиков и цели на минимальное расстояние) в соответствии с алгоритмом, изложенным в пункте 3.3.
|
из
5.00
|
Обсуждение в статье: Шаг 2. Решается задача квадратической минимизации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

