 |
Главная |
Постановка и формализация задач оптимального преследования и уклонения летательных аппаратов
|
из
5.00
|
7.2.1. Краткая характеристика противодействующих объектов
и множеств допустимых управлений
Противодействующими аэродинамическими объектами являются летательный аппарат-перехватчик P и летательный аппарат-цель E. Параметры и координаты перехватчика будут записываться с индексом «Р», а цели – с индексом «Е». В задаче преследования P является союзником, а E – противником.
Известно [143], что для воздействия на величину скорости полета необходимо изменить тангенциальную силу, действующую на ЛА в направлении движения, а для изменения направления полета необходимо приложить к ЛА силу, перпендикулярную вектору скорости, т.е. нормальную силу. Диапазон располагаемых нормальных перегрузок современных целей и ракет-перехватчиков на этапе наведения на порядок шире диапазона располагаемых тангенциальных перегрузок. Это позволяет сделать вывод об эффективности использования нормальных перегрузок для решения типовых задач преследования и уклонения. Поэтому в качестве вектора управления  принимается вектор нормальной перегрузки
принимается вектор нормальной перегрузки 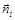 .
.
Для P рассматриваются два возможных способа управления: «управление в полярных координатах» для летательных аппаратов обычной самолетной схемы и «управление в декартовых координатах» для летательных аппаратов с крестообразным крылом.
Для создания нормальной перегрузки требуемой величины  и требуемого направления
и требуемого направления  в обычной самолетной схеме (с крыльями, расположенными в одной плоскости) используются угол атаки
в обычной самолетной схеме (с крыльями, расположенными в одной плоскости) используются угол атаки 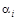 и угол крена
и угол крена  («управление в полярных координатах»). Поскольку между
(«управление в полярных координатах»). Поскольку между  и
и  , а также
, а также  и
и  существуют определенные связи, то вектор
существуют определенные связи, то вектор 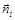 характеризуется величиной нормальной перегрузки
характеризуется величиной нормальной перегрузки  и углом
и углом  , задающим положение
, задающим положение  в плоскости, ортогональной вектору скорости
в плоскости, ортогональной вектору скорости 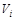 (рис. 7.7).
(рис. 7.7).
Базой для отсчета угла  является вертикальная плоскость. Таким образом, вектор управления имеет вид
является вертикальная плоскость. Таким образом, вектор управления имеет вид
 (7.34)
(7.34)
Множество допустимых управлений  является кругом плоскости, ортогональной вектору
является кругом плоскости, ортогональной вектору  , и определяется следующим образом (рис. 7.8):
, и определяется следующим образом (рис. 7.8):
 . (7.35)
. (7.35)
Угол 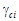 неограничен и его требуемое значение всегда можно найти в диапазоне
неограничен и его требуемое значение всегда можно найти в диапазоне  . Предполагается, что влияние угла скольжения
. Предполагается, что влияние угла скольжения  несущественно и им можно пренебречь.
несущественно и им можно пренебречь.
|
| |
| Рис. 7.7. Введенные системы координат | Рис. 7.8. Допустимое множество |
Для создания нормальной перегрузки требуемой величины и требуемого направления у ЛАi с крестообразным крылом используются угол атаки  и угол скольжения
и угол скольжения  . Поскольку между
. Поскольку между  и
и  , а также между
, а также между  и
и  существуют определенные связи, то вектор
существуют определенные связи, то вектор  создается в результате геометрического сложения перегрузок
создается в результате геометрического сложения перегрузок  и
и  , формируемых в двух взаимно-перпендикулярных плоскостях («управление в декартовых координатах»). Вектор управления имеет вид
, формируемых в двух взаимно-перпендикулярных плоскостях («управление в декартовых координатах»). Вектор управления имеет вид
 (7.36)
(7.36)
где 
При этом накренение ЛА уже не требуется. Более того, предполагается, что угол крена жестко стабилизирован и равен нулю.
Для того чтобы использовать математическое описание вектора управления в виде (7.36) для ЛАi с управлением в «полярных координатах», необходимо определить  по следующим соотношениям:
по следующим соотношениям:
 , (7.37)
, (7.37)
 . (7.38)
. (7.38)
Тогда множество допустимых управлений  вида (7.35) будет определяться
вида (7.35) будет определяться
 , (7.39)
, (7.39)
где символ  обозначает евклидову норму, т.е.
обозначает евклидову норму, т.е.
 . (7.40)
. (7.40)
В качестве ЛА-противника будет всегда рассматриваться объект, для которого известно ограничение на нормальную к вектору скорости 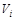 перегрузку. Поэтому и для ЛА-противника вектор управления имеет вид (7.36), а множество допустимых управлений
перегрузку. Поэтому и для ЛА-противника вектор управления имеет вид (7.36), а множество допустимых управлений  имеет вид (7.39).
имеет вид (7.39).
Если длительность этапа управляемого движения невелика, то множества допустимых управлений (множества располагаемых перегрузок)  изменяются незначительно и этими изменениями можно пренебречь.
изменяются незначительно и этими изменениями можно пренебречь.
Алгоритмы преследования и уклонения являются позиционными
«в обратных связях», поэтому возмущения, возникающие в системе P – E из-за неидеальной работы системы стабилизации ЛА-союзника и возможного неоптимального поведения ЛА-противника, учитываются при формировании закона управления.
7.2.2. Уравнения движения
Вводятся в рассмотрение следующие системы координатных осей (рис. 7.7):
·  – нормальная земная система координат (СК), центр которой зафиксирован произвольным образом;
– нормальная земная система координат (СК), центр которой зафиксирован произвольным образом;
·  – нормальная подвижная СК, центр которой совпадает с центром масс Р, а оси параллельны осям нормальной земной СК;
– нормальная подвижная СК, центр которой совпадает с центром масс Р, а оси параллельны осям нормальной земной СК;
·  – определяется аналогично
– определяется аналогично  . Центр совпадает с центром масс Е.
. Центр совпадает с центром масс Е.
· 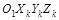 – траекторная подвижная СК, центр которой совпадает с центром масс P, ось
– траекторная подвижная СК, центр которой совпадает с центром масс P, ось  лежит в вертикальной плоскости и может служить для отсчета величины
лежит в вертикальной плоскости и может служить для отсчета величины  , а ось
, а ось 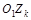 , лежащая в горизонтальной плоскости (
, лежащая в горизонтальной плоскости ( 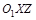 ), образует с осями
), образует с осями  и
и  правую систему;
правую систему;
·  – определяется аналогично СК
– определяется аналогично СК  , но для Е;
, но для Е;
·  – земная неподвижная СК, центр которой с положением центра масс Р в начальный момент времени
– земная неподвижная СК, центр которой с положением центра масс Р в начальный момент времени  , а оси совпадают с осями траекторной СК
, а оси совпадают с осями траекторной СК  ;
;
·  – определяется аналогично СК
– определяется аналогично СК  , но для E.
, но для E.
Координаты центров масс E и P в системе  задаются как
задаются как  – для P и
– для P и  – E. Положение СК
– E. Положение СК  относительно
относительно  задается углами
задается углами  и
и 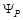 .
.
Углы 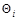 являются углами наклона траекторий ЛА, а
являются углами наклона траекторий ЛА, а  – углами поворота траекторий ЛАi ( i = Р,Е).
– углами поворота траекторий ЛАi ( i = Р,Е).
Положение точки 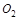 относительно
относительно  задается параметрами
задается параметрами  . Положение точки
. Положение точки 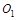 относительно
относительно  задается параметрами
задается параметрами  (на рис. 7.7 не показаны
(на рис. 7.7 не показаны  ).
).
Движение центров масс P и E в системе координат  описывается системой нелинейных дифференциальных уравнений [143]:
описывается системой нелинейных дифференциальных уравнений [143]:
 (7.41)
(7.41)
где  – ускорение свободного падения;
– ускорение свободного падения; 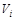 – скорость ЛА.
– скорость ЛА.
Вектор управления ЛАi является двумерным

Ограничение на управление имеет вид (7.39) или (7.36).
При активном маневрировании E на малой высоте полета возможно столкновение с Землей, поэтому необходимо формировать закон управления 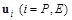 с учетом требования
с учетом требования
 (7.42)
(7.42)
Предполагается, что высота полета P всегда положительна и поэтому подобное ограничение на движение P не накладывается.
7.2.3. Критерии управления
Вектором координат ЛАi в СК  будем называть
будем называть
 (7.43)
(7.43)
Вектором позиции ЛАi в СК будем называть
 (7.44)
(7.44)
где  – вектор скорости ЛАi, а Vi – модуль скорости ЛАi.
– вектор скорости ЛАi, а Vi – модуль скорости ЛАi.
Множество позиционных стратегий ЛАi обозначается
 (7.45)
(7.45)
Множество программных стратегий ЛАi обозначается
 (7.46)
(7.46)
Предполагается, что ЛА-союзнику в каждый момент управляемого движения  точно известны векторы позиций и множества допустимых управлений P и E. Процесс принятия решения от замера позиций до выдачи оптимального управления осуществляется мгновенно. Способы определения векторов позиций рассматриваются ниже.
точно известны векторы позиций и множества допустимых управлений P и E. Процесс принятия решения от замера позиций до выдачи оптимального управления осуществляется мгновенно. Способы определения векторов позиций рассматриваются ниже.
Расстояние между P и E обозначается
 (7.47)
(7.47)
Пусть управляемое движение системы (7.41) началось в некоторый момент времени  , и зона перехвата P имеет радиус действия L.
, и зона перехвата P имеет радиус действия L.
Тогда целью управления P является обеспечение в некоторый момент времени  условия
условия
 (7.48)
(7.48)
которое называется L-встречей, при этом E стремится не допустить выполнения условия (7.48).
Введем критерии управления.
1. Пусть  – момент времени, когда выполняется условие (рис. 7.9)
– момент времени, когда выполняется условие (рис. 7.9)
 . (7.49)
. (7.49)
Конечный промах  определим следующим образом:
определим следующим образом:
 (7.50)
(7.50)
Тогда в качестве первого критерия управления принимается
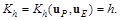 (7.51)
(7.51)

Рис. 7.9. Минимальный промах и время до L-встречи
Таким образом, P стремится достичь минимально-возможного конечного промаха h, а E – наоборот, стремится увеличить конечный промах, причем никаких дополнительных условий на момент  конечного промаха не накладывается.
конечного промаха не накладывается.
2. Пусть  – момент времени, когда впервые выполняется условие (7.48) (рис. 7.9), где
– момент времени, когда впервые выполняется условие (7.48) (рис. 7.9), где
 (7.52)
(7.52)
То есть
 . (7.53)
. (7.53)
P стремится обеспечить выполнение условия (7.48), причем за минимальное время, а E стремится не допустить L-встречи (7.48) или хотя бы отдалить ее во времени. Поэтому в качестве второго критерия управления принимается
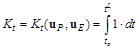 . (7.54)
. (7.54)
Следует заметить, что момент существует всегда, поскольку для каждой пары траекторий P и E всегда найдется момент времени, когда расстояние (7.47) между ними минимально. Момент существует только в том случае, если выполняется условие (7.48), а если 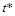 – единственный, то
– единственный, то  .
.
Сформулируем задачи преследования и уклонения в соответствии с введенными критериями  (7.51) и
(7.51) и  (7.54).
(7.54).
Задача 1:  . В классе позиционных стратегий
. В классе позиционных стратегий  требуется найти оптимальное управление
требуется найти оптимальное управление  , удовлетворяющее условию
, удовлетворяющее условию
 (7.55)
(7.55)
и условию (7.42), какими бы ни были начальные позиции объектов.
Вектора управления  являются двумерными
являются двумерными
 . (7.56)
. (7.56)
Допустимые множества управлений  задаются в виде (7.39)
задаются в виде (7.39)
 . (7.57)
. (7.57)
Задача 1:  . Формулируется аналогично задаче 1:
. Формулируется аналогично задаче 1:  , но вместо критерия
, но вместо критерия  используется критерий
используется критерий  (7.54).
(7.54).
Задача 2:  . В классе позиционных стратегий
. В классе позиционных стратегий  требуется найти оптимальное управление
требуется найти оптимальное управление  , удовлетворяющее условию
, удовлетворяющее условию
 (7.58)
(7.58)
и условию (7.42), какими бы ни были начальные позиции объектов. Вектора управления  являются двумерными
являются двумерными
 .
.
Допустимые множества управлений  задаются в виде (7.39).
задаются в виде (7.39).
Задача 2:  . Формулируется аналогично задаче 2:
. Формулируется аналогично задаче 2:  , но вместо критерия
, но вместо критерия  используется критерий
используется критерий  (7.54).
(7.54).
7.2.4. Анализ условий существования равновесия
(седловой точки)
Приведенное ниже доказательство базируется на приведенных в п. 7.1.1 теоремах существования равновесия. В антагонистической дифференциальной игре имеет место равенство
 , (7.59)
, (7.59)
если оптимальные управления 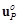 ,
,  доставляют седловую точку [129, 242].
доставляют седловую точку [129, 242].
Соотношение (7.59) соответствует выполнению равенства
 (7.60)
(7.60)
где  – функция Гамильтона для данной игры.
– функция Гамильтона для данной игры.
В случае терминального показателя (7.51)  , гамильтониан имеет вид
, гамильтониан имеет вид
 (7.61)
(7.61)
где  – сопряженный вектор,
– сопряженный вектор,  – векторная запись уравнений (7.51).
– векторная запись уравнений (7.51).
Поскольку движение всей системы (7.41) есть две отдельные траектории P и E (т.е. уравнения, описывающие движения одного объекта, не зависят от вектора управлений другого), то уравнение (7.61) представимо в виде (7.62)
 . (7.62)
. (7.62)
Поскольку 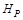 явно зависит только от
явно зависит только от  , а
, а  – только от
– только от 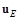 , то
, то
 ; (7.63)
; (7.63)
 . (7.64)
. (7.64)
Таким образом,
 ; (7.65)
; (7.65)
 . (7.66)
. (7.66)
Поскольку правые части уравнений (7.65) и (7.66) равны друг другу и выполняется условие «разделения» (см. замечание 4 в утв. 7.2) и, кроме того, объекты однотипны [98, 129], то, в случае  , имеет место седловая точка.
, имеет место седловая точка.
При интегральном показателе (7.54) 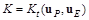 Гамильтониан имеет вид
Гамильтониан имеет вид
 . (7.67)
. (7.67)
Повторяя выкладки (7.62), можно показать, что в случае интегрального критерия также имеет место седловая точка.
Оптимальные стратегии 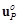 ,
,  , доставляющие седловую точку (7.59), обладают тем свойством, что P (E) невыгодно отклоняться от оптимальной стратегии
, доставляющие седловую точку (7.59), обладают тем свойством, что P (E) невыгодно отклоняться от оптимальной стратегии 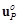 (
(  ), поскольку при таком отклонении выигрыш E (P) только увеличится, а собственный выигрыш уменьшится. Кроме того, оптимальные стратегии
), поскольку при таком отклонении выигрыш E (P) только увеличится, а собственный выигрыш уменьшится. Кроме того, оптимальные стратегии 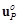 и
и  являются устойчивыми по отношению к получаемой информации об используемой противником стратегии.
являются устойчивыми по отношению к получаемой информации об используемой противником стратегии.
Свойство (7.59) означает, что решение задач преследования может быть получено из известного решения задач уклонения (и наоборот).
Если заменить множества  на
на  (или любое другое), а
(или любое другое), а  на
на  (или любое другое), то свойство (7.59) принимает вид
(или любое другое), то свойство (7.59) принимает вид
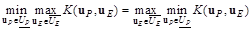 . (7.68)
. (7.68)
Свойство (7.68) будет использовано в дальнейшем.
7.3. Оценка области достижимости центра масс
летательного аппарата со стационарным множеством допустимых управлений
7.3.1. Общая характеристика способа оценки
области достижимости
Область достижимости  в момент времени
в момент времени  из начальной точки
из начальной точки 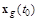 и начального момента
и начального момента  определяется как множество значений вектора координат
определяется как множество значений вектора координат  в момент времени
в момент времени  , полученные при всевозможных допустимых законах управлениях
, полученные при всевозможных допустимых законах управлениях  и начальном условии
и начальном условии 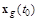 . Динамика области достижимости (ОД) может быть описана динамикой ее границ [193]. Граница ОД определяется траекториями предельного быстродействия [118, 193]. Если движение исследуемого объекта описывается линейной системой уравнений, то существуют относительно простые способы построения границы ОД с использованием фундаментальной матрицы решений [118, 129]. Эта методика существенно использует выпуклость ОД линейных систем. Для нелинейных систем свойство выпуклости ОД, в общем случае, не имеет места. Поэтому для них задача определения границ ОД, или граничных управлений (т.е. приводящих на границу ОД), может быть сформулирована в следующем виде [118, 264]. Необходимо в пространстве координат
. Динамика области достижимости (ОД) может быть описана динамикой ее границ [193]. Граница ОД определяется траекториями предельного быстродействия [118, 193]. Если движение исследуемого объекта описывается линейной системой уравнений, то существуют относительно простые способы построения границы ОД с использованием фундаментальной матрицы решений [118, 129]. Эта методика существенно использует выпуклость ОД линейных систем. Для нелинейных систем свойство выпуклости ОД, в общем случае, не имеет места. Поэтому для них задача определения границ ОД, или граничных управлений (т.е. приводящих на границу ОД), может быть сформулирована в следующем виде [118, 264]. Необходимо в пространстве координат  каким-либо образом задать направление
каким-либо образом задать направление  , например, задав прямую, проходящую через начальное положение центра масс ЛА
, например, задав прямую, проходящую через начальное положение центра масс ЛА  и некоторую другую точку
и некоторую другую точку 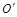 этого пространства (рис. 7.10), и решить две отдельные задачи:
этого пространства (рис. 7.10), и решить две отдельные задачи:
1) найти управление, максимизирующее расстояние  , пройденное объектом за фиксированное время
, пройденное объектом за фиксированное время  в направлении
в направлении  ;
;
2) найти управление, минимизирующее расстояние  , пройденное объектом за фиксированное время
, пройденное объектом за фиксированное время  в направлении
в направлении  .
.
|
| |
Рис. 7.10. Задача достижения экстремума расстояния в направлении  за фиксированное время Т за фиксированное время Т
| Рис. 7.11. Поточечная оценка ОД |
Варьируя направлением  в пространстве координат и каждый раз решая эти две поставленные задачи, можно сделать поточечную [193] оценку ОД для фиксированного
в пространстве координат и каждый раз решая эти две поставленные задачи, можно сделать поточечную [193] оценку ОД для фиксированного  (рис. 7.11).
(рис. 7.11).
При решении обеих задач весьма желательно выявить структурные свойства оптимального в смысле общих критериев (max  и min
и min  ) управления, не зависящие от конкретного направления
) управления, не зависящие от конкретного направления  и времени
и времени  . Знание структуры граничного управления существенно упрощает определение границ ОД в фиксированный момент времени
. Знание структуры граничного управления существенно упрощает определение границ ОД в фиксированный момент времени  . Заметим, что решению задачи минимизации
. Заметим, что решению задачи минимизации  соответствует управление со структурными свойствами предельного быстродействия, а решению задачи максимизации
соответствует управление со структурными свойствами предельного быстродействия, а решению задачи максимизации  – в общем случае, некоторая другая структура управления, которую также необходимо определить.
– в общем случае, некоторая другая структура управления, которую также необходимо определить.
Рассмотрим кратко вопрос существования оптимальных управлений в рамках данных задач.
В общем случае существуют такие направления 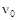 ,
,  , для которых вообще не найдется никаких управлений, удовлетворяющих краевым условиям за фиксированное время
, для которых вообще не найдется никаких управлений, удовлетворяющих краевым условиям за фиксированное время  . Также возможна ситуация, когда существует единственное допустимое управление.
. Также возможна ситуация, когда существует единственное допустимое управление.
В этом случае оно является решением для обеих задач (см.  ,
,  ). Наконец, существуют такие направления (от
). Наконец, существуют такие направления (от 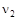 до
до  ), для которых допустимое управление не единственно. Тогда решения поставленных задач существуют и совпадать не могут.
), для которых допустимое управление не единственно. Тогда решения поставленных задач существуют и совпадать не могут.
Формирование управляющего воздействия  или
или  в каждый момент управляемого движения
в каждый момент управляемого движения 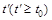 основывается на гипотезе посто-
основывается на гипотезе посто-
янcтва скорости  обоих объектов в прогнозируемом времени
обоих объектов в прогнозируемом времени  на программном такте ПКЗУ
на программном такте ПКЗУ 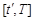 , где
, где  , т.е.
, т.е.  , но вектор скорости изменяется.
, но вектор скорости изменяется.
Кроме того, величина скорости изменяется при изменении программного такта.
Поэтому структуры граничного управления объекта, определяющие поточечную оценку границ  , должны быть найдены с учетом этой гипотезы. Таким образом, динамика центра масс ЛА с постоянной скоростью движения
, должны быть найдены с учетом этой гипотезы. Таким образом, динамика центра масс ЛА с постоянной скоростью движения 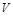 в нормальной земной СК
в нормальной земной СК 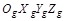 описывается дифференциальными уравнениями
описывается дифференциальными уравнениями
 (7.69)
(7.69)
|
| |
| Рис. 7.12. Области суб- и супер-достижимости | Рис. 7.13. Новые множества допустимых управлений |
Используя подход [183, 258], определим понятия субдостижимости  , супердостижимости
, супердостижимости 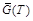 следующим образом:
следующим образом:
 . (7.70)
. (7.70)
Здесь  – область достижимости объекта (7.69). Таким образом, субдостижимость
– область достижимости объекта (7.69). Таким образом, субдостижимость  оптимально оценивает ОД ЛА
оптимально оценивает ОД ЛА  снизу и дает гарантированную оценку того, что
снизу и дает гарантированную оценку того, что  заведомо не меньше, чем
заведомо не меньше, чем  .
.
Супердостижимость  оптимально оценивает ОД ЛА
оптимально оценивает ОД ЛА  сверху и дает гарантированную оценку того, что
сверху и дает гарантированную оценку того, что  заведомо не больше, чем
заведомо не больше, чем 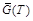 (рис. 7.12). На рис. 7.12
(рис. 7.12). На рис. 7.12  – символ границы области
– символ границы области  .
.
Учитывая минимаксный или максиминный характер решаемых задач, для игрока-союзника необходимо использовать оценку снизу – субдостижимость 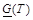 , а для игрока-противника – использовать оценку сверху – супердостижимость
, а для игрока-противника – использовать оценку сверху – супердостижимость  .
.
Проведем анализ системы (7.69), учитывая, что:
 ; (7.71)
; (7.71)
 (7.72)
(7.72)
Располагаемая перегрузка  определяет максимально возможную, нормальную к скорости
определяет максимально возможную, нормальную к скорости  , перегрузку, действующую на ЛА в процессе полета при отсутствии ускорения свободного падения
, перегрузку, действующую на ЛА в процессе полета при отсутствии ускорения свободного падения  . Оно изменяет максимально возможную нормальную перегрузку на величину
. Оно изменяет максимально возможную нормальную перегрузку на величину  :
:
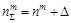 , (7.73)
, (7.73)
причем
 . (7.74)
. (7.74)
Введем обозначение (рис. 7.15)
 ; (7.75)
; (7.75)
 , (7.76)
, (7.76)
тогда 
или
 (7.77)
(7.77)
Таким образом, в процессе полета максимально возможная действующая на ЛА нормальная перегрузка будет не меньше величины  (оценка снизу), но и не больше величины
(оценка снизу), но и не больше величины  (оценка сверху). Это позволяет получить новое математическое описание движения центра масс ЛА для определения его суб- и супердостижимости, которое в нормальной земной неподвижной СК
(оценка сверху). Это позволяет получить новое математическое описание движения центра масс ЛА для определения его суб- и супердостижимости, которое в нормальной земной неподвижной СК 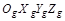 имеет следующий вид:
имеет следующий вид:
 (7.78)
(7.78)
Ограничения на управление имеют вид
 (7.79)
(7.79)
и
 (7.80)
(7.80)
– для определения субдостижимости, или
 (7.81)
(7.81)
– для определения супердостижимости.
Необходимо отметить, что описание в виде (7.69) будет справедливым для любой неподвижной СК (в том числе и для 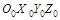 , поскольку сила тяжести в уравнениях отсутствует (но ее действие учтено в ограничениях (7.80) и (7.81)).
, поскольку сила тяжести в уравнениях отсутствует (но ее действие учтено в ограничениях (7.80) и (7.81)).
Направление  однозначно определяется прямой (
однозначно определяется прямой ( 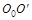 ). Координаты точки
). Координаты точки 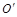 в СК
в СК  обозначим
обозначим 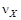 ,
,  ,
,  .
.
Введем угол  , определяемый согласно
, определяемый согласно
 =
=  . (7.82)
. (7.82)
Введем дополнительные СК (рис. 7.14, 7.15):
·  – неподвижная земная СК, задаваемая поворотом системы
– неподвижная земная СК, задаваемая поворотом системы  вокруг оси
вокруг оси  на угол
на угол  ;
;
·
|
из
5.00
|
Обсуждение в статье: Постановка и формализация задач оптимального преследования и уклонения летательных аппаратов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы





