Пример 1. Рассмотрим алгебру множеств – модель булевой алгебры.

А £ В если А Ì В.

1. А Ú В=В

2. А Ù В=А

3. А Ú В= U

4. А Ù В `= Æ

Любая конечная булева алгебра может содержать лишь 2 в степени n элементов, где n – натуральное число.

Пример 2. 1)Множество делителей 70-ти D =<1,2,5,7,10,14,35,70>. Множество A =<2,5,7> -множество атомов решетки D .

10 = 2 Ú 5

14 = 2 Ú 7

35 =5 Ú 7

70 = (2 Ú 5) Ú 7

    70

10  14 35

 

2  5  7

 

    1

2) Множество А = {2,5,7}    

Отношение вложенности.

     {2,5,7}

{2,5} {2,7} {5,7}

 {2} {5}  {7}

         Æ

Эта решетка изоморфна предыдущей.

Алгебра множеств и алгебра высказываний являются моделями абстрактной булевой алгебры. Все абстрактные булевы алгебры (которые состоят из одинакового числа элементов) изоморфны.

 

1.3Минимальные формы булевых многочленов

Определение. Понятие булева многочлена определяется рекурсивно. Пусть Х _n = { x ₁ ,…, x_n } – множество из n символов (называемых неизвестными или переменными), которое не содержит символов 0 и 1. Булевы многочлены над Х _n суть объекты, которые могут быть получены последовательным применением следующих правил:

(I) х₁, х₂, …, х _n , 0,1 – булевы многочлены;

(II) если p и q – булевы многочлены, то таковыми являются и

( p ) Ù ( q ), ( p ) Ú ( q ), ( p ) ¢ .

Обозначим множество всех булевых многочленов над Х _n через Р _n.

Пример. Вот несколько примеров булевых многочленов над {х₁, х₂}: 0,1, х₁, х_2, х₁ Ù х₂, х₁ Ú х₂, х₁ ¢ , х₁ ¢ Ù х₂.

Так как любой булев многочлен над x ₁ ,…, x_n модно рассматривать как булев многочлен над x ₁ ,…, x_n , x_{n +1}, мы имеем

Р₁ Ì Р₂ Ì … Ì Р _n Ì Р _{n +1} Ì …

Булев многочлен можно упростить с помощью аксиом булевой алгебры. В процессе упрощения часто трудно решить, какие аксиомы и в каком порядке должны быть использованы. Но существуют некоторые систематические методы упрощения булевых многочленов. Недостатком большинства этих методов является возможность их практического внедрения, когда число переменных слишком велико. Соответствующая проблематика в теории булевых алгебр носит общее название проблема оптимизации или минимизации булевых многочленов; она важна для таких приложений, как упрощение переключательных схем.

Определение.  Назовем литералом любую переменную х _i и ее дополнение  х _i ¢, а также 0 и 1. Под произведением понимается произведение нескольких литералов, т.е. булев многочлен, в котором нет знака +. Дизъюнктивным выражением или просто выражением назовем буле многочлен, являющийся суммой произведений. Слагаемые в таком выражении назовем дизъюнктами.

Обсуждая упрощение булевых многочленов, мы ограничимся важным случаем сведения дизъюнктивных выражений к «минимальным выражениям» относительно специального условия минимальности. Обозначим через d_f общее число литералов в выражении f, а через e_f – число дизъюнктов. Мы говорим, что выражение f проще выражения j, если d_f £ d_g , e_f £ e_g и хотя бы одно из этих неравенств строгое. Выражение f называется минимальным, если не существует выражения, которое было бы эквивалентно f и проще f. Таким образом, мы будем искать «кратчайшее» выражение с наименьшим возможным числом литералов, которое было бы эквивалентно f. Такое минимальное выражение не всегда определено однозначно. Я опишу один из нескольких существующих методов упрощения. Он основан на работе Куайна и был улучшен Мак-Класки, поэтому называется методом Куайна - Мак-Класки.

Определение. многочлен p влечет многочлен q, если для любых b ₁ ,…., b_n Î В

р_в ( b ₁ , …, b_n ) = 1 влечет q _в ( b ₁ , …, b_n ) = 1;

в этом случае р называется импликантом для q. Простым импликантом многочлена р называется произведение 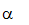, которое влечет р, но если в 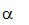вычеркнуть хотя бы один сомножитель, то результат уже не влечет р. Произведение, сомножители-литералы которого образуют подмножество сомножителей-литералов другого произведения, называется подпроизведением последнего.

Пример. Произведение х₁х₃ является подпроизведением как х₁х₂х_3, так и х₁х₂ ¢ х₃, и влечет выражение

р = х₁х₂х₃ + х₁х₂ ¢ х₃ + х₁ ¢ х₂ ¢ х₃ ¢ ,

поскольку (х₁х₃)(1, i ₂ , 1) = 1 и р(1, i ₂ , 1) = 1, а для других значений аргументов х₁х₃ дает 0. Ни х_1, ни х₃ не влекут р; например, х₁(1, 1, 0) = 1, но р(1, 1, 0) = 0, поэтому х₁х₃ – простой импликант для р.

Теорема. Любой многочлен р Î P_n эквивалентен сумме всех своих простых импликантов.

Выражение, являющееся суммой простых импликантов для р, называется неприводимым, если оно эквивалентно р, но пересекает быть таковым, если удалить хотя бы одно слагаемое. Минимальное выражение должно быть неприводимым. Поэтому, чтобы определить минимальное выражение, мы находим все неприводимые выражения, а среди них ищем выражение с наименьшим числом литералов. Изложим теперь принадлежащий Куайну метод определения простых импликантов.

Простые импликанты получаются из дизъюнктивной нормальной формы d булева многочлена р применением (слева направо) правила

yz + yz ¢ ~ y ,

когда это возможно. Более общо, мы используем правило

   (*)

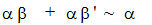где 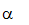и - произведения. следующий пример поможет понять смысл описываемой процедуры.

Пример. Пусть р – булев многочлен, имеющий следующую дизъюнктивную нормальную форму:

d = wxyz ’ + wxy ’ z ’ + wx ’ yz + wx ’ yz ’ + w ’ x ’ yz + w ’ x ’ yz ’ + w ’ x ’ y ’ z

Мы используем правило и законы идемпотентности для тех (из общего числа ( 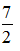) = 21) пар дизъюнктов в d, для которых это возможно, тем самым «укорачивая» произведения. например, превый и второй дизъюнкты при использовании (*) дают wxz ’. Если в процессе упрощения слагаемые используются хотя бы один раз, то оно помечается. Так как знак + стоит вместо Ú, выражение может быть использовано любое число раз, но помечается не более одного раза. Таким образом, все помеченные произведения содержат более короткие произведения и поэтому не могут быть простыми импликантами. В целом в первом раунде этого процесса мы переходим

от wxyz ’ и wxy ’ z ’ к wxz ’

от wx ’ yz и wx ’ yz ’ к wx ’ y

от wxyz ’ и wx ’ yz ’ к wyz ’

от w ’ x ’ yz и w ’ x ’ yz ’ к w ’ x ’ y

от w ’ x ’ yz и w ’ x ’ y ’ z к w ’ x ’ z

от wx ’ yz и w ’ x ’ yz к x ’ yz

от wx ’ yz ’ и w ’ x ’ yz ’ к x ’ yz ’

Здесь использованы, и потому должны быть помечены, все семь слагаемых.

В общем, эта процедура повторяется снова и снова с использованием только помеченных выражений (которые становятся короче). Прочие произведения суть простые импликанты и остаются неизменными.

В нашем примере второй раунд упрощения осуществляет переход

от wx ’ y и w ’ x ’ y к x ’ y

от x ’ yz и x ’ yz ’ к x ’ y

Четыре выражения - wx ’ y, w ’ x ’ y, x ’ yz, x ’ yz ’ – помечены. Остальные произведения, а именно wxz ’, wyz ’, w ’ x ’ z не могут быть упрощен. следовательно, р эквивалентно такой сумме простых импликантов:

р ~ wxz ’ + wyz ’ + w ’ x ’ z + x ’ y .

Как уже было сказано, Мак-Класки улучшил это метод. Чтобы описать улучшенный алгоритм, используем многочлен

d = wxyz ’ + wxy ’ z ’ + wx ’ yz + wx ’ yz ’ + w ’ x ’ yz + w ’ x ’ yz ’ + w ’ x ’ y ’ z

Шаг 1. Считая переменные упорядоченными по алфавиту (или по номерам), поставим в соответствие каждому произведению последовательность символов из {0, 1, -}: вместо x_i ’ и x_i запишем 0 и 1 соответственно, а вместо опущенных переменных запишем черточку. Например, вместо w ’ x ’ y ’ z запишем 0001, а вместо w ’ x ’ z – 00-1.

Шаг 2. Произведения, рассматриваемые как троичные n-ки, разбиваются на классы эквивалентности в соответствии с числом единиц. Упорядочим классы по возрастанию этого числа. В нашем примере:

w ’ x ’ y ’ z 0 0 0 1

w ’ x ’ yz ’0 0 1 0

w ’ x ’ yz 0 0 1 1

wx ’ yz ’1 0 1 0

wx ’ yz 1 0 1 1

wxyz ’1 1 1 0

wxy ’ z ’1 1 0 0

Шаг 3.Используя правило (*), нужно складывать только произведения из соседних классов, т.е. когда числа единиц в соответствующих последовательностях отличаются лишь на 1. При этом мы должны сравнивать выражения из соседних классов, имеющих черточки в одних и тех же позициях. Если два таких выражения отличаются точно в одной позиции, то они имеют вид р = i ₁ i ₂ … i_r … i_n и q = i ₁ i ₂ … i_r ’… i_n, где все i_k лежат в {0, 1, -}, а i_r лежит в {0, 1}. Тогда (*) сводит p, q к i ₁ i ₂ … i_{r -1} - i_{r +1} … i_n, причем p и q должны быть помечены. В рассматриваемом примере это дает такие четверки (метки относятся к следующему раунду, тогда как в предыдущем списке все произведения следовало пометить):

0 0 - 1

0 0 1 - ü

- 0 1 0 ü

- 0 1 1 ü

1 0 1 - ü

1 - 1 0

1 1 - 0

Помеченные выражения не являются простыми импликантами и во втором раунде этого шага дают единственное выражение

- 0 1 -

Итак, мы нашли все простые импликанты, а именно

0 0 1 - w’x’z

- 0 1 0 wyz’

- 0 1 1 wxz’

1 0 1 - x’y

Так как сумма всех простых импликантов необязательно является минимальным выражением, алгоритм требует выполнения ещё одного шага.

Шаг 4. В силу теоремы сумма всех простых импликантов для р эквивалентна р. поэтому для каждого слагаемого дизъюнктивной нормальной формы d многочлена р должен существовать простой импликант, являющийся произведением этого слагаемого. для выявления возникшего соответствия удобно использовать таблицу простых импликантов. столбцы этой таблицы индексируются дизъюнктами из d, а строки – простыми импликантами, вычисленными в шаге 3. на пересечении i -й строки и j-го столбца ставится крестик û, если простой импликант из i -й строки является подпроизведением произведения из j-го столбца. Говорят, что одно произведение покрывает, если первое является подпроизведением второго. Для того, чтобы найти сумму простых импликантов, которая будет эквивалентна d , мы из множества всех простых импликантов выбираем подмножество таким образом, чтобы каждое слагаемое в d покрывалось по крайней мере одним импликантом из подмножества. Тогда минимальной формой будет сумма простых импликантов с наименьшим числом членов и наименьшим числом букв. Простой импликант называется главным членом, если он покрывает произведение, не покрываемое никаким другим простым импликантом; сумма всех главных членов называется ядром. сначала мы находим ядро, затем обозначаем через q ₁ ,…, q_k произведения, не покрываемые простыми импликантами из ядра; простые импликанты, не входящие в ядро, обозначим через р₁,…,р _m. Далее формируем таблицу, столбцы которой индексируются элементами q_i, а строки – элементами р _i. Крестик û на месте (i , j) указывает, что р_i покрывает q_j .

Теперь образуем произведение сумм. Каждый сомножитель соответствует одному из q_j и является суммой тех р_i, который покрывают этот q_j. Используя законы булевой алгебры, мы преобразуем это выражение в простейшую возможную сумму произведений. Каждое из этих произведений представляет подмножество элементов р _i, которые покрывают все q_j. Далее рассматриваем произведения с наименьшим числом сомножителей. Из этих кратчайших произведений выбираем те, что содержат наименьшее общее число литералов. Теперь каждое из полученных произведений переписываем в виде суммы составляющих его простых импликантов, складываем с ядром, получая минимальную сумму произведений, эквивалентную р.