 |
Главная |
Лабораторная работа №9. Решение задачи нелинейного программирования методом штрафных функций
|
из
5.00
|
Рассмотрим пример из п.6.8.
Метод реализован в Straf.pas.
Описание типов.
TPoint = Array of Extended – для хранения вектора значений.
TPurposeFunction = Function (P: TPoint): Real – целевая функция.
TQ = Array of Function (P: TPoint): Real – массив ограничений.
TB = Array of Real – правые части ограничений.
TdF = Array of Function (P: TPoint): Real – производные целевой функции.
TdQ = Array of Array of Function (P: TPoint): Real – производные ограничений.
Используемые глобальные переменные:
- PurposeFunction: TPurposeFunction – хранит целевую функцию;
- IterCount: Integer – хранит количество итераций.
Описаны следующие функции.
Функция Function CurrentStraf (var P: TPoint; L: TPoint; Q: TQ; B: TB; dF: TdF; dQ: TdQ; Lambda: Real; E: Real ): Real – реализует метод Штрафных функций. Возвращает оптимальное значение функции.
Параметры функции:
- P – на входе содержит начальную точку, на выходе получает оптимальную точку;
- L – содержит весовые коэффициенты;
- Q – содержит матрицу коэффициентов системы ограничений;
- B – содержит правые части ограничений;
- dF – содержит производные целевой функции;
- dQ – содержит производные ограничений;
- Lambda – содержит штрафной параметр;
- E – задает точность вычислений.
Текст программы.
unit Straf;//Метод штрафных функций
{****************************************************************************
Целевая функция описывается в вызывающем модуле , переменной PurposeFunction
присваивается имя функции в вызывающем модуле. Для запуска метода должны быть
описаны : начальная точка, функции ограничения, правые части ограничений,
производные целевой функции по каждой переменной, производные каждого ограничения
по каждой переменной, заданы весовые коэф-ты, штрафной параметр Lambda.
*****************************************************************************}
interface
Type
TPoint = Array of Real; //Тип массив значений всех переменных
TPurposeFunction = Function(P : TPoint) : Real; //Тип целевая функция
TQ = Array of Function(P : TPoint) : Real;// Массив функций - ограничений
TB = Array of Real;//Массив Bi - правая часть в ограничениях
TdF = Array of Function(P : TPoint) : Real;//Массив производных целевой
//функции по всем переменным
TdQ = Array of Array of Function(P : TPoint) : Real;//Производные
// каждого ограничения по каждой переменной
Var PurposeFunction : TPurposeFunction;//Целевая функция
IterCount : Integer;
{*****************************Процедура поиска***********************************************}
Function CurrentStraf(var P : TPoint;L : TPoint;Q : TQ; B : TB; dF : TdF; dQ : TdQ; Lambda : Real;E : Real ) : Real;
//P - Задается начальная точка, на выходе содержит значение конечной точки
//L - Весовые коэффициенты
//Q - Ограничения
//B - Правые части ограничений
//dF - Производные целевой функции
//dQ - Производные ограничений
//Lambda - штрафной параметр
//E - заданная точность
implementation
Function NormaV(P1,P2 : TPoint) : Real; //Нахождение нормы ветора,
//заданного разницей векторов P1 и P2
Var I : Integer;
Begin
Result:=abs(P1[0]-P2[0]);
For I:=1 to High(P1) do If abs(P1[I]-P2[I])>Result Then Result:=abs(P1[I]-P2[I]);
End;
{***Проверка векторов-градиентов целевой функции и функций-ограничений на коллинеарность*******}
Function Collin(P : TPoint;dF : TdF; dQ : TdQ; E : Real) : Boolean;
//P - Текущая точка
//dF - Производные целевой функции
//dQ - Производные ограничений
//E - Степень точности
Var I,J : Integer;
gradF : Array of Real;//Градиент целевой функции
gradQ : Array of Array of Real;//Градиенты ограничений
TT : Array Of Real;
Begin
SetLength(gradF,High(P)+1);
SetLength(TT,High(P)+1);
SetLength(gradQ,High(dQ)+1,High(P)+1);
For I:=0 to High(P) do
Begin
gradF[I]:=dF[I](P);//Вычисление градиента целевой функции в текущей точке
End;
For I:=0 to High(dQ) do //Цикл по функциям - ограничениям
Begin
For J:=0 to High(P) do //Цикл по каждой переменной I-ой функции
Begin
GradQ[I][J]:=dQ[I][J](P);//Вычисление градиентов функций-ограничений в текущей точке
End;
End;
{Result:=True;
For I:=0 to High(P) do //Номер переменной целевой функции
For J:=0 to High(dQ) do //Номер ограничения
For K:=1 to High(P) do //Номер переменной в J-ом ограничении
If (GradQ[J][0]=0) OR (GradQ[J][K]=0) Then Begin Result:=False;Exit; End Else
if (GradF[I]/GradQ[J][0])-(GradF[I]/GradQ[J][K])>E Then Result:=False; }
Result:=True;
For I:=0 to High(P) do //Номер переменной целевой функции
For J:=0 to High(dQ) do //Номер ограничения
TT[I]:=(GradF[I]/GradQ[J][I]);
For I:=1 To High(TT) do
if (TT[0]-TT[I])>E Then Result:=False;
End;
Function CurrentStraf;
Var I,J : Integer;
Li : Real;//Текущий весовой коффициент
P1,P2 : TPoint;//Новая точка
dQSum : Real;//Сумма производных ограничений по текущей
// переменной в текущей точке
g : Real;
Begin
SetLength(P1,High(P)+1);
SetLength(P2,High(P)+1);
P2:=Copy(P);
For I:=0 to High(P) do
Begin
dQSum:=0;
For J:=0 to High(Q) do
Begin
{Если точка находится в области допустимых решений то текущий весовой коэффециент равен нулю}
If B[J]-Q[J](P)>=0 Then Li:=0 Else Li:=L[J];
dQSum:=dQSum+Li*dQ[J][I](P);//Вычисление второго слагаемого
End;
P1[I]:=P[I]+Lambda*(dF[I](P)+dQSum);//Переход к новой точке
If P1[I]<0 Then P1[I]:=0;//Выбирается максимум из 0 и P1[I]
//и заносится в P1[I]
End;
G:=0;
For I:=0 to High(Q) do G:=G+B[I]-Q[I](P1);
IterCount:=1;
While (Abs(G)>E) And (Not Collin(P1,dF,dQ,E)) do //Пока вектора
//градиенты не будут коллинеарны...
Begin
P:=Copy(P1); //Переход к новой текущей точке
For I:=0 to High(P) do
Begin
dQSum:=0;
For J:=0 to High(Q) do
Begin
If B[J]-Q[J](P)>=0 Then Li:=0 Else Li:=L[J];
dQSum:=dQSum+Li*dQ[J][I](P);//Вычисление второго слогаемого
End;
P1[I]:=P[I]+Lambda*(dF[I](P)+dQSum);//Переход к новой точке
If P1[I]<0 Then P1[I]:=0;//Выбирается максимум из 0 и P1[I] и заносится в P1[I]
End;
Inc(IterCount);
G:=0;
For I:=0 to High(Q) do G:=G+B[I]-Q[I](P1);
End;
P:=Copy(P1);
Result:=PurposeFunction(P);//Вычисление значения целевой функции
// в точке максимума
End;
end.
Результат работы программы.
Оптимальное решение: x=(0.670,0.669).
Оптимальное значение функции: 0,442.
Варианты заданий.
1  2
2 







 3
3  4
4 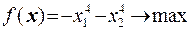

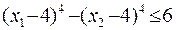


5 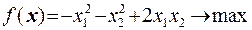 6
6 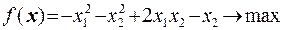






7  8
8 
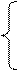




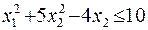


9 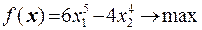 10
10 


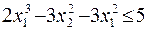
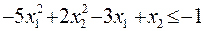




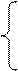
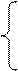 11
11 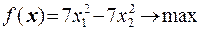 12
12 

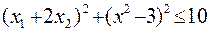

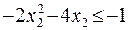


13 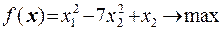 14
14 
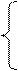
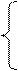

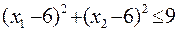
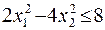
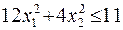


 15
15 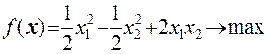 16
16 
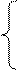
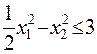
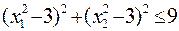



17 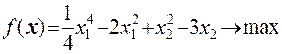 18
18 








 20
20  19
19 






 21
21  22
22 


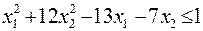
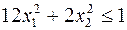
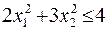
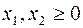

23 



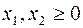
 24
24 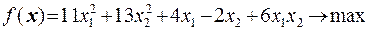
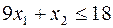

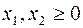
 25
25 
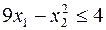
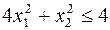
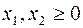
26 


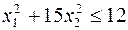

27 




28 
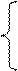


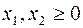
 29
29 



30 
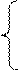


|
из
5.00
|
Обсуждение в статье: Лабораторная работа №9. Решение задачи нелинейного программирования методом штрафных функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

