Метод скользящего суммирования.

       Задана стандартная последовательность статистически независимых случайных чисел {x_i} с нулевым математическим ожиданием и единичной дисперсией.

        Необходимо найти алгоритм формирования из неё последовательности чисел {y_i} с заданной корреляционной функцией и нормальным распределением. Воспользуемся для этого формулой скользящего суммирования

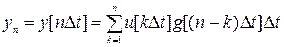 или

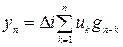            (1)

в развернутом виде , видно что процесс {y_k} получается скользящим суммированием {u_k} с весом g_n-k.      

В соответствии с этой формулой последовательность {y_i} формируется следующим образом:

y₁=С₁x₁+ С₂x₂+…+ С_nx_n,

y₂=С₁x₂+ С₂x₃+…+ С_nx_n+1, (2)

y_i=С₁x_i+ С₂x_i+1+…+ С_nx_n+i-1.

Отсюда для i-того дискретного значения получаем 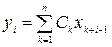            (3)

Если число слагаемых достаточно велико (n>8), то согласно центральной предельной теореме {y_i} можно считать последовательностью с нормальным распределением. Как видно из (3), задача формирования {y_i} с заданной корреляционной функцией R(τ) сводится к определению коэффициентов C_k. Для расчета C_k можно воспользоваться несколькими методами, в частности:

       а) решать нелинейную систему алгебраических уравнений с помощью соотношения (2);

       б) разлагать спектральную плотность G(ω) в ряд Фурье.          

       Рассмотрим первый метод. Вычислим корреляционную функцию ряда {y_i}. Для i=1 из (3) получаем R[0]= 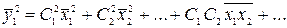Так как {x_i} имеет единичную дисперсию, 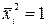, а поскольку x_i (i= 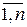) - статистически независимые, 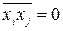. Поэтому

,

,

,

………………………………………………………

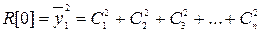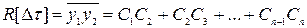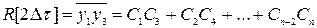………………………………………………………                   (4)       

,

,

.

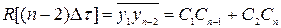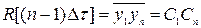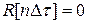Мы получаем систему n нелинейных алгебраических уравнений относительно коэффициентов 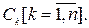 Левая часть уравнений определяется дискретными значениями R[iΔτ], аппроксимирующими заданную корреляционную функцию R(τ) (рис. 2), и поэтому считается известной. В результате решения этой системы можно найти все n коэффициентов C_k.

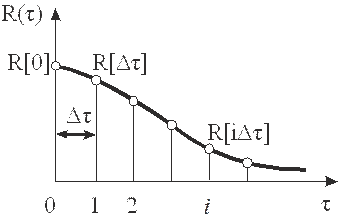
Рис. 2.

Пример. 1. Алгоритм цифрового моделирования нормального процесса с корреляционной функцией треугольной формы (рис. 3). В этом случае

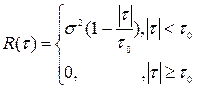.     (5)

где τ₀ - время корреляции моделируемого процесса. Нетрудно убедиться, что все коэффициенты C_k здесь оказываются одинаковыми и для определения одного из них достаточно воспользоваться любым уравнением системы (4). Например, из первого уравнения получаем

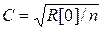,    (6)       

где в соответствии с (5) 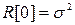. Число n суммируемых дискретных значений исходного процесса {x_i} выбирается из условия достаточно хорошей аппроксимации корреляционной функции R(τ) её дискретными значениями R[iΔτ]. В общем случае n=τ₀/Δτ (рис. 3), следовательно,

.

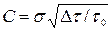Отсюда алгоритм формирования случайной последовательности в соответствии с (3) имеет вид

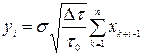       (7)

При цифровом моделировании случайного процесса y(t) интервал дискретизации по времени Δt при формировании ординат y_i следует выбирать из условия Δt<<τ₀, где τ₀ – время корреляции.

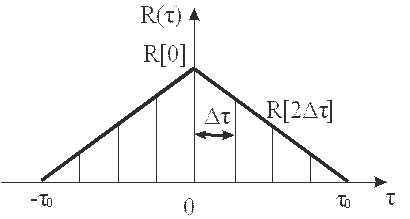
Рис. 3.

       Рассмотрим вычисление коэффициентов C_k вторым способом. Воспользуемся для этого соотношением , определяющим структуру формирующего фильтра. Для четного K(jω) импульсная реакция такого фильтра

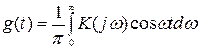. (8)

Случайный процесс на выходе при белом шуме на входе описывается выражением

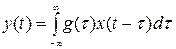. (9)

Предположим, что спектр G(ω) импульсной реакции g(t) ограничен частотой ω_Г и спектр шума x(t) также ограничен. Тогда в соответствии с теоремой Котельникова подынтегральную функцию можно заменить дискретным рядом ординат, следующих через интервалы Δt=π/ω_Г. Тогда в соответствии с формулой (1) интеграл (9) можно точно представить суммой

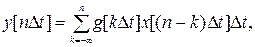
где Δt=π/ω_Г. Отсюда

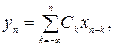  (10)

Где 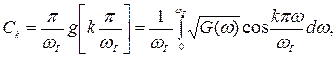(11)

 

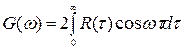                                             (12)

Таким образом, для заданной корреляционной функции R(τ) вначале находим G(ω), затем C_k и далее последовательность y_n.

       Пример. 2. Моделирование «белого» шума.

       При формировании идеального белого шума на ЦВМ выборки независимых дискретных значений случайных чисел пришлось бы брать через бесконечно малые интервалы Δt, что практически нереализуемо. Поэтому задачу о моделировании на ЦВМ белого шума решают приближенно, выбирая независимые случайные числа через конечные интервалы Δt. Чтобы шум можно было считать белым, его спектр G(ω) в полосе пропускания исследуемой системы должен быть равномерным, а ширина спектра должна значительно превышать шумовую полосу системы.

       Спектральная плотность последовательности импульсов со случайной амплитудой и фиксированной длительностью Δt (рис. 4) определяется соотношением

G(ω)=(σ²_x/ω²Δt)(1-cosωΔt),        (13)

где σ²_x – дисперсия исходной последовательности чисел {x_i}. В области нулевых частот спектральная плотность этой последовательности

G(0)=2σ²_xΔt.        (14)

Отсюда находим дисперсию σ²_x случайных чисел {x_i} при заданной спектральной плотности G(0) дискретного процесса и выбранном интервале дискретизации.

       Подставляя (14) в (11), после интегрирования получаем

С_k=(2σ²_xΔt/kπ)sinkπ.

Это соотношение совместно с (10) образует алгоритм формирования на ЦВМ белого шума.

 

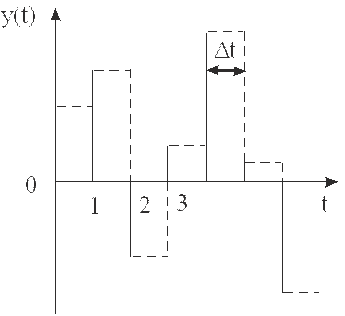
Рис. 4.

Примеры моделирования случайных величин.

Пример 1. Листинг программы моделирования последовательности случайных величин с равномерным законом распределения.

      

 

Пример 2. Листинг программы моделирования последовательности случайных величин с распределением Рэлея.

 

 

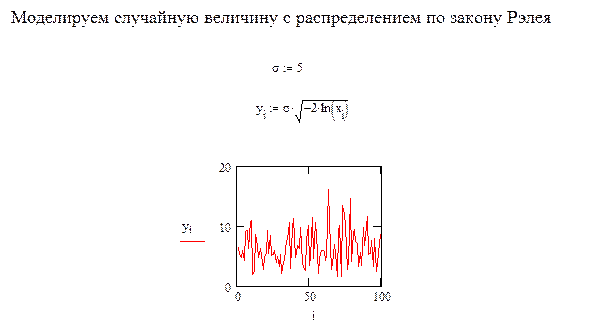
Лекцию разработал

Доцент к.т.н. доцент       В. Ерохин

26.06.2014