Способы описания дискретных систем

Дискретные системы, как и аналоговые, могут описываться различными способами. Благодаря сходству свойств z-преобразования со свойствами преобразований Лапласа и Фурье способы описания аналоговых и дискретных систем в основном похожи друг на друга.

Так же, способ описания системы характеризует ее структурную схему

Импульсная характеристика

В случае линейных систем с постоянными параметрами для анализа прохождения любого сигнала достаточно знать результат прохождения элементарного импульса в виде дельта-функции. Для дискретных систем также можно ввести в рассмотрение единичную импульсную функцию x(k₀)

Выходная реакция на единичный импульс x(k₀), определяемая при нулевых начальных условиях, называется импульсной характеристикой дискретной системы и обозначается h(k).

Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик

Функция передачи

Применим z-преобразование к уравнению дискретной фильтрации (свертки импульсной характеристики и входного сигнала). Так как это уравнение представляет собой дискретную свертку, то, согласно свойствам z-преобразования, результатом будет являться произведение z-преобразований:

Y(z) = X(z) H(z).

Отсюда выразим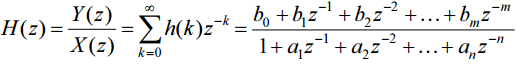

Таким образом, функция передачи физически реализуемой дискретной системы может быть представлена в виде отношения полиномов по отрицательным степеням переменной z

Связь структурной схемы и функции передачи

Еще раз вспомним свойства Z преобразований: задержка и линейность

Задержка

, оператор z^-k0 – оператор задержки

Линейность

Исходя из этих свойств, мы можем представить сигналы, как сумму этих же сигналов, умноженных на единичную функцию с соответствующей задержкой. А структуру фильтра представить в следующем виде:

Согласно свойствам z-преобразования, задержка дискретной последовательности на один такт соответствует умножению ее z-преобразования на z–1. Поэтому элементы памяти, осуществляющие такую задержку, обозначены на структурной схеме как z^–1.

Данная схема представляет собой рекурсивный фильтр (фильтр, имеющий бесконечную импульсную характеристику)

Если в вычислении выходного отсчета участвуют только входные отсчеты в текущий и предыдущий моменты времени, и НЕ участвуют выходные отсчеты, то такой фильтр называют нерекурсивный или "трансверсальный фильтр" (от английского transversal — поперечный)

Уравнение фильтрации в этом случае приобретает следующий вид:

Количество используемых предыдущих отсчетов m называется порядком фильтра (filter order).

ЗАМЕЧАНИЕ

Следует обратить внимание на различие между терминами порядок фильтра и длина фильтра. Под длиной фильтра имеется в виду общее число отсчетов, участвующих в вычислениях, включая текущий отсчет x(k), поэтому длина дискретного фильтра на единицу больше, чем его порядок.

Структурная схема приведена на рисунке. Некоторое количество предыдущих отсчетов входного сигнала хранится в ячейках памяти,

которые образуют дискретную линию задержки. Эти отсчеты умножаются на коэффициенты b_i и суммируются, формируя выходной отсчет y(k).

Импульсная характеристика нерекурсивного фильтра определяется очень просто. Подставим в уравнение фильтрации единичный импульс x(k₀) в качестве входного сигнала:

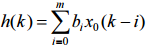
Но отсчет x₀(k-i) − равен нулю для всех k, кроме k = i, когда этот отсчет равен единице. Поэтому мы получаем очень простой результат:

h(k)=b_k

то есть коэффициенты b_i являются отсчетами импульсной характеристики фильтра. Это можно наглядно пояснить с помощью изображения структурной схемы. При подаче на вход единичного импульса он будет перемещаться по линии задержки, умножаться на коэффициенты b0 , b1 , b2 , ... и проходить на выход устройства (ведь все остальные входные сигналы сумматора при этом равны нулю). Очевидно, что в реальном устройстве линия задержки содержит конечное число элементов, поэтому импульсная

характеристика нерекурсивного фильтра также является конечной по длительности.

Это обусловило еще одно название таких фильтров — фильтры с конечной импульсной характеристикой (КИХ-фильтры; английский термин — finite impulse response, FIR).

Следует отметить:

Вследствие отсутствия обратных связей любой нерекурсивный фильтр является устойчивым — ведь каковы бы ни были начальные условия (т. е. отсчеты, хранящиеся в линии задержки), при отсутствии сигнала на входе (x(k) = 0) выходной сигнал (свободные колебания) будет отличен от нуля в течение не более чем m тактов, необходимых для очистки линии задержки.

Простота анализа и реализации, а также наглядная связь коэффициентов фильтра с отсчетами его импульсной характеристики и абсолютная устойчивость привели к тому, что нерекурсивные фильтры широко применяются на практике. Однако для получения хороших частотных характеристик (например, полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры высокого порядка — до нескольких сотен и даже тысяч.

Симметричные фильтры

Очень важное значение имеет тот факт, что нерекурсивные фильтры позволяют легко обеспечить линейную ФЧХ, а значит, постоянные (не зависящие от частоты) групповую и фазовую задержки. Для этого необходима лишь симметрия импульсной характеристики. Эта симметрия может быть двух типов:

- четная симметрия (even symmetry): b _k =b_N-k  для всех k = 0, 1, ..., N;

- нечетная симметрия (odd symmetry): b _k = -b_N-k  для всех k = 0, 1, ..., N.

Иногда под симметричными подразумевают только характеристики с четной симметрией, а для нечетной симметрии используют термин антисимметричные" .

Доказать линейность ФЧХ для симметричных фильтров очень легко, если воспользоваться для этого свойствами преобразования Фурье. Действительно, их импульсные характеристики представляют собой четные или нечетные (в зависимости от типа симметрии) функции, сдвинутые вправо на N/2 отсчетов. Спектр четной функции является чисто вещественным, а нечетной — чисто мнимым, временной сдвиг же приводит к появлению в ФЧХ слагаемого, линейно зависящего от частоты. Таким образом, ФЧХ симметричных фильтров описывается следующим образом:

Групповая задержка для симметричных фильтров не зависит от частоты и равна N/2 отсчетам.

При четном N и нечетной симметрии импульсной характеристики, очевидно, ее средний отсчет должен быть равен нулю: b_N/2 = 0. Кроме того, четность или нечетность порядка фильтра и наличие того или иного типа симметрии накладывают определенные ограничения на коэффициенты передачи фильтра на нулевой частоте и на частоте Найквиста. Эти ограничения легко получить из условий симметрии и формулы комплексного коэффициента передачи фильтра.

 Сочетание четности порядка фильтра и типа симметрии дает четыре типа симметричных фильтров.

Приведенные в таблице номера типов часто используются в зарубежной литературе.