 |
Главная |
Указания к выполнению контрольной работы
|
из
5.00
|
Критерий Сильвестра
1. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы главные миноры
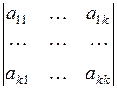
матрицы А квадратичной формы были положительны для всех k = 1, 2, …, n.
2. Для отрицательной определенности квадратичной формы необходимо и достаточно, чтобы главные миноры нечетного порядка были отрицательны, а четного – положительны.
Указания к выполнению контрольной работы
1. Вариант задания контрольной работы определяется преподавателем.
2. Контрольная работа выполняется в школьной тетради, на обложку которой наклеивается титульный лист. Образец титульного листа приведен на последней странице.
3. На каждой странице тетради оставляются поля размером 3 см (для замечаний и пояснений преподавателя).
4. При выполнении контрольной работы необходимо придерживаться последовательности задач, данных в задании.
5. Перед решением каждой задачи ее условие переписывается полностью.
6. Решение задач следует излагать подробно, сопровождая необходимыми объяснениями; выполнять чертежи, если это требуется заданием.
7. По получении прорецензированной, но не зачтенной работы, все необходимые исправления и дополнения следует сделать на последующих после рецензии страницах этой же тетради.
Варианты контрольной работы
1. Даны матрицы
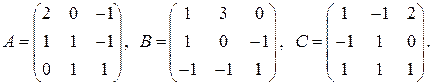
Найти:
| 1.1. 2CT + BA. | 1.2. AB + 2CT. |
| 1.3. AB – 8CT. | 1.4. BC + 3AT. |
| 1.5. AC – 5BT. | 1.6. AC + 2BT. |
| 1.7. BC – 6AT. | 1.8. CA – 5BT. |
| 1.9. CTA – 2B. | 1.10. AB – 4CT. |
| 1.11. AB – 3CT. | 1.12. AB + 3CT. |
| 1.13. AB – 5CT. | 1.14. CB + 3AT. |
| 1.15. AB – 6CT. | 1.16. BC + 2AT. |
| 1.17. CB – 3AT | 1.18. 5BT – AC. |
| 1.19. AB – 2CT. | 1.20. CB + 3AT. |
2. Решить систему линейных уравнений матричным способом и по формулам Крамера:
2.1. 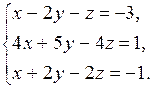
| 2.2. 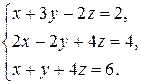
| 2.3. 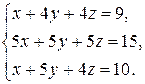
|
2.4. 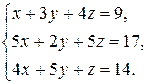
| 2.5. 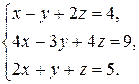
| 2.6. 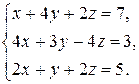
|
2.7. 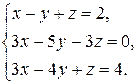
| 2.8. 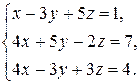
| 2.9. 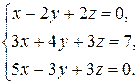
|
2.10. 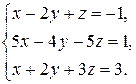
| 2.11. 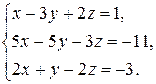
| 2.12. 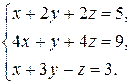
|
2.13. 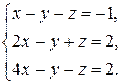
| 2.14. 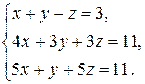
| 2.15. 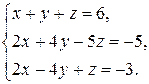
|
2.16. 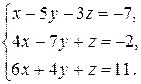
| 2.17. 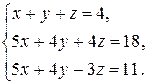
| 2.18. 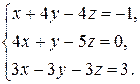
|
2.19. 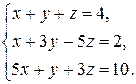
| 2.20. 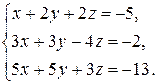
|
3. Пусть A , B, C – вершины треугольника ABC. Найти:
1) внутренний угол при вершине А;
2) проекцию вектора 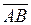 на вектор
на вектор 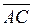 ;
;
3) длину медианы АМ.
Сделайте чертеж.
| 3.1. A(–4, 4), B(3, 9), C(10, –6). | 3.2. A(–3, 4), B(6, 12), C(15, –12). |
| 3.3. A(–1, 1), B(2, 8), C(5, –13). | 3.4. A(–1, 1), B(2, 9), C(5, –15). |
| 3.5. A(–3, 3), B(5, 12), C(13,–15). | 3.6. A(–3, 3), B(2, 8), C(7, –7). |
| 3.7. A(–2, 4), B(5, 8), C(12, –4). | 3.8. A(–2, 2), B(6, 8), C(14, –10). |
| 3.9. A(–5, 5), B(5, 10), C(15, –5). | 3.10. A(–1, 5), B(4, 9), C(9, –3). |
| 3.11. A(–3, 5), B(4, 9), C(11, –3). | 3.12. A(–3, 3), B(4, 9), C(11, –9). |
| 3.13. A(–4, 4), B(2, 9), C(8, –6). | 3.14. A(–3, 3), B(2, 9), C(7, –9). |
| 3.15. A(– 4, 5), B(3, 9), C(10, –3). | 3.16. A(–3, 5), B(2, 11), C(7, –7). |
| 3.17. A(–3, 5), B(2, 9), C(7, –3). | 3.18. A(–3, 3), B(3, 9), C(9, –9). |
| 3.19. A(–4, 1), B(4, 8), C(12, –13). | 3.20. A(–4, 5), B(2, 10), C(8, –5). |
4. Даны координаты вершин пирамиды ABCD. Найти:
1) площадь грани ABC;
2) объем пирамиды;
3) длину высоты D H, опущенной из вершины D на грань ABC.
4.1. A(1, –2, 4), B(–4, 3, 0), C(2, 3, 2), D(6, 0, 6).
4.2. A(4, –3, 4), B(0, –1, 3), C(6, 2, –1), D(7, 0, 5).
4.3. A(2, –4, 5), B(–2, –1, 2), C(4, 0, 2), D(5, 0, 7).
4.4. A(2, –1, 5), B(–3, 1, 1), C(7, 4, 3), D(3, 3, 7).
4.5. A(2, –1, 3), B(–3, 0, 0), C(7, 4, 2), D(5, 3, 4).
4.6. A(2, –4, 5), B(–2, –1, 2), C(4, 0, 2), D(5, 0, 7).
4.7. A(5, –3, 2), B(2, –2, 0), C(9, 2, –2), D(10, 1, 5).
4.8. A(1, –3, 4), B(–3, –2, 2), C(6, 1, 3), D(3, 1, 6).
4.9. A(2, –5, 3), B(–1, –2, 1), C(4, –1, –2), D(3, –2, 8).
4.10. A(5, –5, 4), B(2, –3, 0), C(6, –3, 1), D(7, 0, 6).
4.11. A(5, –5, 1), B(2, –4, –1), C(8, –2, 0), D(7, 0, 5).
4.12. A(4, –3, 5), B(0, 2, 1), C(9, –1, 4), D(7, –2, 7).
4.13. A(3, –2, 3), B(0, 1, 2), C(5, 1, 0), D(7, 2, 8).
4.14. A(5, –5, 1), B(0, –1, –2), C(10, 0, –2), D(7, –4, 2).
4.15. A(4, –4, 2), B(3, –2, –1), C(6, 1, –1), D(9, –2, 6).
4.16. A(3, –4, 2), B(0, –2, 0), C(6, 0, –2), D(8, –2, 5).
4.17. A(1, –4, 1), B(–1, –1, –4), C(4, 1, –3), D(4, –1, 6).
4.18. A(5, –1, 3), B(0, 1, –1), C(8, 0, 2), D(10, 0, 4).
4.19. A(4, –2, 4), B(0, 2, 1), C(7, 3, 1), D(9, 2, 7).
4.20. A(4, –5, 1), B(3, –1, –2), C(5, –4, –1), D(6, –1, 6).
5. Даны вершины треугольника ABC .
Найти:
1. уравнение стороны АВ треугольника;
2. уравнение медианы АМ;
3. уравнение высоты CD;
4. длину высоты CD;
5. уравнение прямой проходящей через вершину А параллельно
стороне ВС.
5.1. A(–2, 2), B(6, 8), C(14, –10).
5.2. A(–1, 1), B(2, 8), C(5, –13).
5.3. A(–3, 3), B(4, 9), C(11, –9).
5.4. A(– 4, 5), B(3, 9), C(10, –3).
5.5. A(–2, 4), B(5, 8), C(12, –4).
5.6. A(–3, 5), B(2, 9), C(7, –3).
5.7. A(–3, 3), B(3, 9), C(9, –9).
5.8. A(–1, 5), B(4, 9), C(9, –3).
5.9. A(–4, 4), B(3, 9), C(10, –6).
5.10. A(–3, 4), B(6, 12), C(15, –12).
5.11. A(–4, 5), B(2, 10), C(8, –5).
5.12. A(–1, 1), B(2, 9), C(5, –15).
5.13. A(–4, 1), B(4, 8), C(12, –13).
5.14. A(–3, 3), B(2, 8), C(7, –7).
5.15 A(–5, 5), B(5, 10), C(15, –5).
5.16. A(–3, 3), B(5, 12), C(13, –15).
5.17. A(–3, 5), B(2, 11), C(7, –7).
5.18 A(–3, 3), B(2, 9), C(7, –9).
5.19. A(–4, 4), B(2, 9), C(8, –6).
5.20. A(–3, 5), B(4, 9), C(11, –3).
6. Даны координаты вершин пирамиды ABCD .
Найти:
1. уравнения ребер АВ, АС и AD;
2. уравнение грани ABC;
3. уравнения и длину высоты D H, опущенной из вершины D на грань ABC;
4. уравнение плоскости, проходящей через вершину D параллельно грани АВС.
6.1. A(1, –2, 4), B(–4, 3, 0), C(2, 3, 2), D(6, 0, 6).
6.2. A(2, –1, 5), B(–3, 1, 1), C(7, 4, 3), D(3, 3, 7).
6.3. A(5, –5, 4), B(2, –3, 0), C(6, –3, 1), D(7, 0, 6).
6.4. A(1, –3, 4), B(–3, –2, 2), C(6, 1, 3), D(3, 1, 6).
6.5. A(2, –1, 3), B(–3, 0, 0), C(7, 4, 2), D(5, 3, 4).
6.6. A(5, –3, 2), B(2, –2, 0), C(9, 2, –2), D(10, 1, 5).
6.7. A(2, –5, 3), B(–1, –2, 1), C(4, –1, –2), D(3, –2, 8).
6.8. A(4, –3, 4), B(0, –1, 3), C(6, 2, –1), D(7, 0, 5).
6.9. A(4, –5, 1), B(3, –1, –2), C(5, –4, –1), D(6, –1, 6).
6.10. A(3, –4, 5), B(0, 0, 2), C(5, –1, 4), D(6, 0, 6).
6.11. A(2, –4, 5), B(–2, –1, 2), C(4, 0, 2), D(5, 0, 7).
6.12. A(3, –4, 2), B(0, –2, 0), C(6, 0, –2), D(8, –2, 5).
6.13. A(5, –1, 3), B(0, 1, –1), C(8, 0, 2), D(10, 0, 4).
6.14. A(5, –5, 1), B(0, –1, –2), C(10, 0, –2), D(7, –4, 2).
6.15. A(4, –3, 5), B(0, 2, 1), C(9, –1, 4), D(7, –2, 7).
6.16. A(4, –2, 4), B(0, 2, 1), C(7, 3, 1), D(9, 2, 7).
6.17. A(3, –2, 3), B(0, 1, 2), C(5, 1, 0), D(7, 2, 8).
6.18. A(1, –4, 1), B(–1, –1, –4), C(4, 1, –3), D(4, –1, 6).
6.19. A(5, –5, 1), B(2, –4, –1), C(8, –2, 0), D(7, 0, 5).
6.20. A(4, –4, 2), B(3, –2, –1), C(6, 1, –1), D(9, –2, 6).
7. Найти собственные значения и собственные векторы матрицы:
7.1. 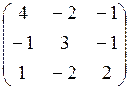 7.2.
7.2. 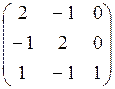
7.3. 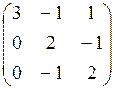 7.4.
7.4. 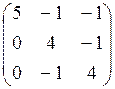
7.5. 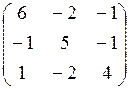 7.6.
7.6. 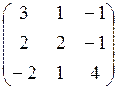
7.7. 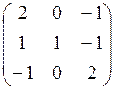 7.8.
7.8. 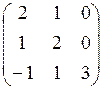
7.9. 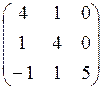 7.10.
7.10. 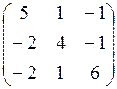
7.11. 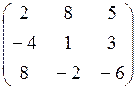 7.12.
7.12. 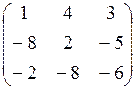
7.13. 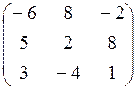 7.14.
7.14. 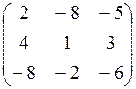
7.15. 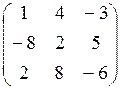 7.16.
7.16. 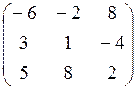
7.17. 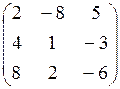 7.18.
7.18. 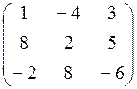
7.19. 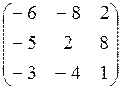 7.20.
7.20. 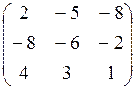
8. Исследовать на знакоопределенность квадратичную форму.
8.1. 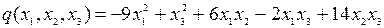
8.2. 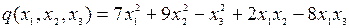
8.3. 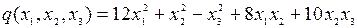
8.4. 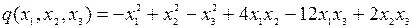
8.5. 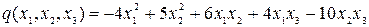
8.6. 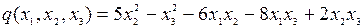
8.7. 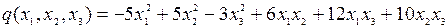
8.8. 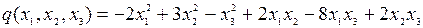
8.9. 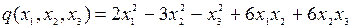
8.10. 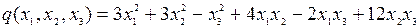
8.11. 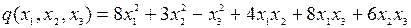
8.12. 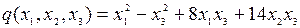
8.13. 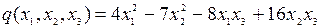
8.14. 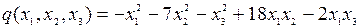
8.15. 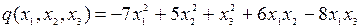
8.16. 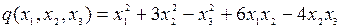
8.17. 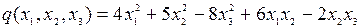
8.18. 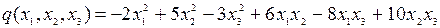
8.19. 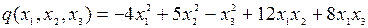
8.20. 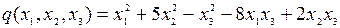
Ниже приводится порядок и методика решения типовых задач из контрольной работы.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Вариант № 0
1.0. Даны матрицы: 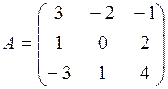 ,
, 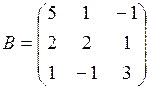 ,
, 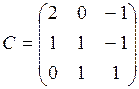 . Найти
. Найти 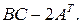
Решение.
1) Находим 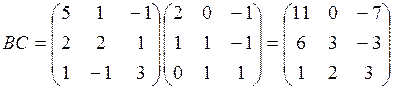
2) Находим 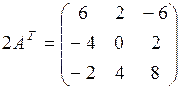 .
.
3) 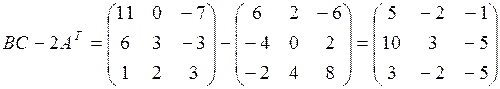 .
.
Ответ: 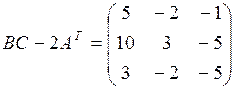 .
.
2.0. 1) Решить систему
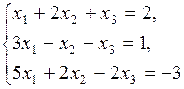
матричным способом.
Решение. Запишем ее в матричной форме
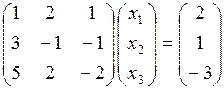 или AX = B.
или AX = B.
Решение системы будет иметь вид:
X = A–1B = 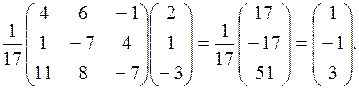
Следовательно, x1 = 1, x2 = –1, x3 = 3.
Ответ: (1, –1, 3).
2) Решить систему линейных уравнений
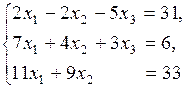
по формулам Крамера.
Решение.
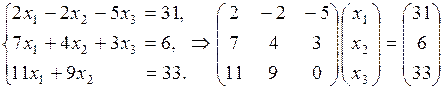 .
.
Формулы Крамера: 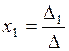 ,
, 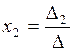 ,
, 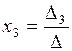 .
.
Вычислим определители:
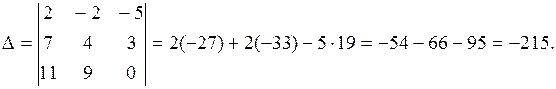
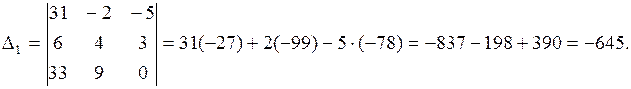
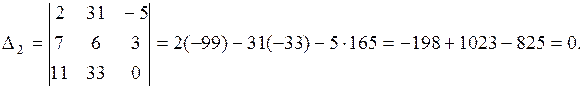
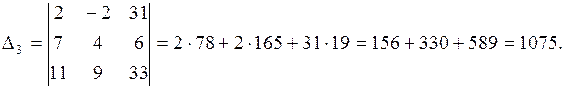
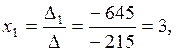
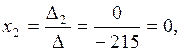
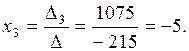
Ответ: (3, 0, –5).
3.0. Пусть A(–1, 1), B(1, –1), C(5, 1) – вершины треугольника ABC. Найдите:
1) внутренний угол при вершине А;
Решение. Найдем координаты векторов 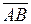 и
и 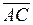 :
:
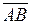 = (1 – (–1), –1 –1) = (2, –2),
= (1 – (–1), –1 –1) = (2, –2), 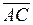 = (5 – (–1), 1 – 1) = (6, 0).
= (5 – (–1), 1 – 1) = (6, 0).
Тогда внутренний угол при вершине A есть угол между векторами 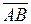 и
и 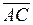 .
.
По формуле 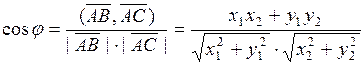
находим 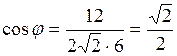 ,
, 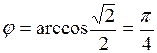 .
.
Ответ: 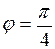 .
.
2) проекцию вектора 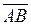 на вектор
на вектор 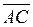 ;
;
Решение. По формуле 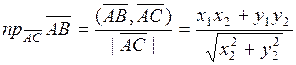
получаем 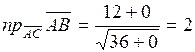 .
.
Ответ: 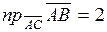 .
.
3) длину медианы АМ.
Решение. Точка M делит отрезок BC пополам, следовательно, отношение BM к MC равно 1, то есть l = 1. Определим координаты точки M по формулам
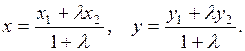
Получаем 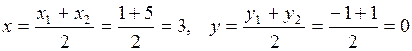 , то есть M(3, 0).
, то есть M(3, 0).
Найдем координаты вектора 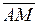 = (3 – (–1), 0 – 1) = (4, –1).
= (3 – (–1), 0 – 1) = (4, –1).
Длину медианы АМ вычислим по формуле 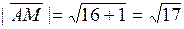 .
.
Ответ: 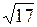 .
.
4.0. Даны координаты вершин пирамиды ABCD: A(4, 2, –2), B(5, 3, 1),
C(6, 1, –1), D(3, –1, –2). Найти:
1) площадь грани ABC;
Решение. Найдем площадь грани АВС как площадь треугольника. Вычислим координаты  = (1, 1, 3) и
= (1, 1, 3) и 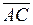 = (2, –1, 1).
= (2, –1, 1).
Затем 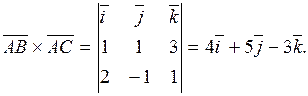
Откуда 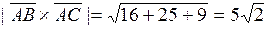 . Тогда
. Тогда 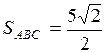 .
.
Ответ: 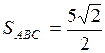 .
.
2) объем пирамиды;
Решение. Найдем координаты векторов 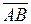 ,
, 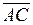 и
и 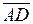 :
:
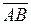 = (1, 1, 3),
= (1, 1, 3), 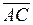 = (2, –1, 1),
= (2, –1, 1), 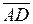 = (–1, –3, 0).
= (–1, –3, 0).
ABCD – пирамида с треугольным основанием, то есть тетраэдр. Тогда
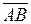
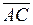
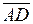 =
= 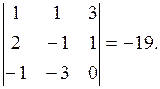
Следовательно, 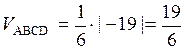 .
.
Ответ: 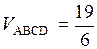 .
.
3) длину высоты D H, опущенной из вершины D на грань ABC.
Решение. Объем тетраэдра ABC можно вычислить по формуле VABCD = 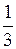 × ×SABC×D H, где DH – высота, опущенная из вершины D на грань ABC. Тогда
× ×SABC×D H, где DH – высота, опущенная из вершины D на грань ABC. Тогда
DH = 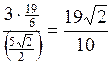 .
.
Ответ: DH = 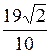 .
.
5.0 Дан треугольник АВС с вершинами в точках: А(3, –2), В(5, 1), С(2, 6). Найти:
1) уравнение стороны АВ.
Решение.
Запишем уравнение прямой, проходящей через две точки А(3, –2), В(5, 1):
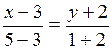 или
или 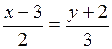
3(x – 3) = 2(y + 2);
3x – 2y – 13 = 0
– уравнение прямой, проходящей через точки А и В.
Ответ: 3x – 2y – 13 = 0.
2) уравнение медианы АМ;
Решение.
Так как M середина BC, то M(3,5; 3,5). Запишем уравнение прямой, проходящей через две точки А и M: 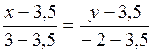 или y + 11x – 42 = 0.
или y + 11x – 42 = 0.
Ответ: y + 11x – 42 = 0.
3) уравнение высоты CD;
Решение. Для высоты CD вектор 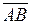 является нормальным, запишем уравнение прямой с нормальным вектором.
является нормальным, запишем уравнение прямой с нормальным вектором.
Координаты вектора 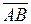 = (5 – 3, 1 + 2) = (2, 3). Тогда уравнение высоты, проходящей через точку С:
= (5 – 3, 1 + 2) = (2, 3). Тогда уравнение высоты, проходящей через точку С:
2(x – 2) + 3(y – 6) = 0;
2x + 3y – 22 = 0.
Ответ: 2x + 3y – 22 = 0.
4) длину высоты CD;
Решение. Длину высоты CD найдем как расстояние от прямой АВ до точки С: 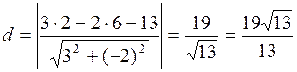 .
.
Ответ: 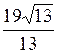 .
.
5) уравнение прямой проходящей через вершину А параллельно стороне ВС.
Решение. Для прямой проходящей через вершину А параллельно стороне ВС, вектор 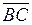 является направляющим, запишем уравнение прямой с направляющим вектором.
является направляющим, запишем уравнение прямой с направляющим вектором.
Координаты вектора  = (2 – 5, 6 – 1) = (–3, 5). Тогда уравнение искомой прямой:
= (2 – 5, 6 – 1) = (–3, 5). Тогда уравнение искомой прямой:
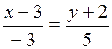 .
.
Ответ: 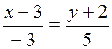
6.0. Даны координаты вершин пирамиды А(1, –1, 1), В(3, 1, –1), С(2, 2, 3), D(3, 4, 5). Найти:
1) уравнения ребра АВ;
Решение. Запишем уравнение прямой в пространстве через две точки 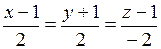 .
.
Ответ: 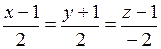 .
.
2) уравнение грани АВС;
Решение.
Запишем уравнение плоскости, проходящей через три точки А, В и С:
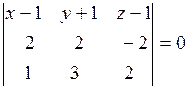 .
.
Разложив определитель по первой строке, получим уравнение плоскости 5x – 3y +2z – 10 = 0.
Ответ: 5x – 3y +2z – 10 = 0.
3) уравнение и длину высоты D H, опущенной из вершины D на грань ABC;
Решение.
Из уравнения грани ABC имеем координаты направляющего вектора высоты DH: 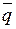 = (5, –3, 2).
= (5, –3, 2).
Запишем канонические уравнения прямой, проходящей через точку D параллельно вектору 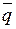 :
:
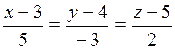 .
.
Ответ: 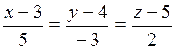 .
.
4) уравнение плоскости, проходящей через вершину D параллельно грани АВС.
Решение.
Воспользуемся уравнением плоскости, проходящей через точку D и перпендикулярной вектору 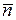 =
= 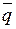 = (5, –3, 2):
= (5, –3, 2):
5(x – 3) – 3(y – 4) + 2(z – 5) = 0 или 5x – 3y + 2z – 13 = 0.
Ответ: 5x – 3y + 2z – 13 = 0.
7.0. Пусть в пространстве L линейный оператор 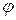 задан матрицей
задан матрицей
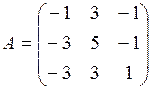 .
.
Найти собственные значения и векторы оператора 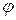 (матрицы A).
(матрицы A).
Решение. Составим характеристическое уравнение
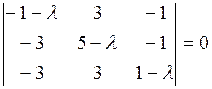
или l3 – 5l2+ 8l – 4 = 0, (l – 1)(l2 – 4l + 4) = 0.
Решениями последнего уравнения будут l1 = 1, l2 = 2, l3 = 2, которые являются собственными числами оператора 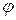 (число 2 – кратный корень характеристического уравнения).
(число 2 – кратный корень характеристического уравнения).
Далее поступаем следующим образом:
1) Берем l = 1 и подставляем в матричное уравнение (*) на стр.17. Получаем
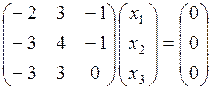 .
.
Решая ее методом Гаусса, получаем x1 = x2 = x3 = t. Тогда собственному значению l = 1 соответствуют собственные векторы 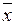 = (t, t, t) = t(1, 1, 1,), где t – любое число не равное нулю.
= (t, t, t) = t(1, 1, 1,), где t – любое число не равное нулю.
2) Подставляем теперь в (*) значение l = 2:
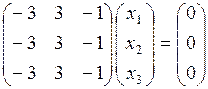 .
.
Что эквивалентно одному уравнению –3x1 + 3x2 – x3 = 0. Находим его общее решение x1 = x2 – 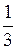 x3. Полагая x2 = u, x3 = 3v, получаем собственные векторы оператора j
x3. Полагая x2 = u, x3 = 3v, получаем собственные векторы оператора j
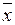 = (u – v, u, v),
= (u – v, u, v),
отвечающие собственному значению l = 2, где u и v могут принимать любые действительные значения не равные одновременно нулю.
8.0. Исследовать на знакоопределенность квадратичную форму
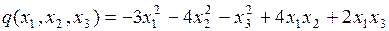 .
.
Решение. Запишем матрицу квадратичной формы
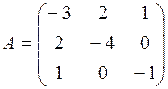 .
.
Вычисляем главные миноры:
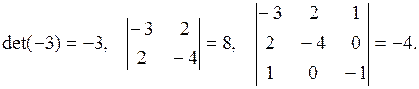
Следовательно, квадратичная форма – отрицательно определенная.
Ответ: квадратичная форма является отрицательно определенной.
ПРИЛОЖЕНИЕ
ОБРАЗЕЦ ТИТУЛЬНОГО ЛИСТА
Министерство образования и науки России
Рыбинский государственный авиационный технический университет
имени П. А. Соловьева
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Вариант № ____
Выполнил (а) _________________
(Ф.И.О.)
студент (ка) гр. _____, ____ курса
Преподаватель ________________
(Ф.И.О.)
Оценка –
Подпись преподавателя ________
Дата _________________________
Рыбинск 20__
|
из
5.00
|
Обсуждение в статье: Указания к выполнению контрольной работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

