 |
Главная |
Определитель матрицы. Обратная матрица
|
из
5.00
|
Матрицы
Определители
Практикум
Матрицы и действия над ними
Размерностью матрицы (обозначается  ) называется количество её строк
) называется количество её строк  и столбцов
и столбцов  .
.
1) Сложение матриц:
Суммой двух матриц  и
и  одинаковой размерности называется матрица
одинаковой размерности называется матрица  той же размерности, элементы которой определяются по формулам :
той же размерности, элементы которой определяются по формулам :
 (1.1)
(1.1)
 . Для обозначения суммы матриц используют запись
. Для обозначения суммы матриц используют запись  .
.
Свойства сложения матриц:
1. Коммутативности  ;
;
2. Ассоциативности  .
.
Эти свойства позволяют нам не заботиться о порядке следования слагаемых матриц.
2) Умножение матрицы на число:
Произведением матрицы  на вещественное число l называется матрица
на вещественное число l называется матрица  той же размерности, что и матрица
той же размерности, что и матрица  , элементы которой определяются по формуле:
, элементы которой определяются по формуле:
 (1.2)
(1.2)
 . Для обозначения произведения матрицы на число используется запись
. Для обозначения произведения матрицы на число используется запись  .
.
Свойства умножения матрицы на число:
1. Ассоциативности относительно числового множителя:  ;
;
2. Дистрибутивности относительно суммы чисел:  ;
;
3. Дистрибутивности относительно суммы матриц:  .
.
Из операции умножения матрицы на число можно определить разность матриц как  .
.
3) Транспонирование матриц:
Матрица  называется транспонированной к матрице
называется транспонированной к матрице  (обозначается
(обозначается 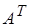 ) если ее элементы определяются по правилу:
) если ее элементы определяются по правилу:
 (1.3)
(1.3)
 .
.
Свойства операции транспонирования матрицы:
1)  ;
;
2) 
3)  .
.
4) Перемножение матриц:
Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  элементы которой определяются по формуле:
элементы которой определяются по формуле:
 (1.4)
(1.4)
 . Матрица
. Матрица  называется произведением матрицы
называется произведением матрицы  и
и  что записывается
что записывается  .
.
Из формулы  видно, что матрицы перемножаются только в том случае, когда число столбцов первой матрицы, совпадает с числом строк второй матрицы.
видно, что матрицы перемножаются только в том случае, когда число столбцов первой матрицы, совпадает с числом строк второй матрицы.
Формулу (1.4) можно рассматривать как совокупность скалярных произведений вектор-строк матрицы  на вектор-столбцы матрицы
на вектор-столбцы матрицы  .
.
Свойства перемножения матриц:
1)  - свойство ассоциативности;
- свойство ассоциативности;
2)  - свойство дистрибутивности относительно суммы матриц;
- свойство дистрибутивности относительно суммы матриц;
3)  - свойство ассоциативности относительно числового множителя;
- свойство ассоциативности относительно числового множителя;
4)  - свойство антикоммутативности.
- свойство антикоммутативности.
Практикум
1. Вычислить  :
:
1)  ,
,  ,
,  .
.
2)  ,
,  ,
,  .
.
2. Для данных матриц:
а) проставить размерность;
в) протранспонировать матрицы;
с) перемножить, если это возможно.
1)  ,
,  ,
,  ,
,  ;
;
 .
.
2)  ,
,  ,
,  ,
, 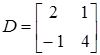 ;
;  .
.
3. Решение типового задания
1. Для данных матриц  ,
,  ,
,  вычислить
вычислить  :
:
Решение:
Прежде чем производить линейные действия над матрицами, необходимо убедится в том, что их размерности совпадают. Все три матрицы имеют размерности  по количеству строк и столбцов соответственно. Действия выполняем согласно формулам (1.1) и (1.2).
по количеству строк и столбцов соответственно. Действия выполняем согласно формулам (1.1) и (1.2).
 .
.

 .
.
Для данных матриц  ,
,  ,
,  ,
,  ,
,
 .
.
а) проставить размерность; б) протранспонировать матрицы;
в) перемножить, если это возможно.
Решение:
а) Размерность матрицы определяется количеством её строк и столбцов. Матрица 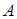 имеет две строки и два столбца, матрица
имеет две строки и два столбца, матрица  - две строки и один столбец, и т.д. Поэтому:
- две строки и один столбец, и т.д. Поэтому:
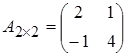 ,
,  ,
,  ,
,  ,
,  .
.
б) Протранспонируем заданные матрицы. Для этого соответствующие строки матриц запишем столбцами:  ,
,  ,
,  ;
;  ,
,  .
.
в) Рассмотрим операцию перемножения. Перемножить можно лишь те матрицы в которых количество строк первой матрицы совпадает с количеством столбцов второй матрицы.
Матрица А имеет размерность  , а матрица
, а матрица  – размерность
– размерность  , поэтому матрицы перемножить можно и в результате перемножения мы получаем матрицу-столбец размерности соответствующей крайним индексам матриц
, поэтому матрицы перемножить можно и в результате перемножения мы получаем матрицу-столбец размерности соответствующей крайним индексам матриц  и
и  :
:  .
.
 .
.
Рассмотрим подробно вычисление элементов матрицы  . Данная матрица в символьном виде записывается так:
. Данная матрица в символьном виде записывается так:  . Она состоит из двух элементов обозначенных индексами:
. Она состоит из двух элементов обозначенных индексами:  и
и  .
.
1) Для первого элемента  и
и 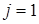 , тогда формула (1.4) примет вид:
, тогда формула (1.4) примет вид:  . Индекс суммирования
. Индекс суммирования  , изменяется от
, изменяется от  до
до  т.е. суммирование элементов производится по внутренним индексам (они подчеркнуты). Распишем сумму:
т.е. суммирование элементов производится по внутренним индексам (они подчеркнуты). Распишем сумму:
 .
.
Для следующего элемента поступаем аналогично:
 .
.
2) Перемножение матриц можно определить через скалярное произведение вектор-строки матрицы  на вектор-столбец матрицы
на вектор-столбец матрицы  . Для нахождения элемента
. Для нахождения элемента  возьмем первую вектор-строку матрицы
возьмем первую вектор-строку матрицы  и умножим её скалярно на первый вектор-столбец матрицы
и умножим её скалярно на первый вектор-столбец матрицы  :
:
 ;
;
 .
.
Т.е. матрицы умножаются 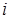 -ая строка на
-ая строка на  -ый столбец.
-ый столбец.
В обратном порядке эти матрицы перемножать нельзя. Произведение 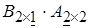 не определено, т.к. внутренние индексы (они подчеркнуты) различны и мы не можем произвести по ним суммирование.
не определено, т.к. внутренние индексы (они подчеркнуты) различны и мы не можем произвести по ним суммирование.
Перемножим теперь матрицы  и
и  . Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности
. Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности  .
.
Матрица  в символьном виде записывается так:
в символьном виде записывается так:
 .
.
Необходимо определить шесть элементов  , для этого возьмем соответствующую
, для этого возьмем соответствующую  -ую строку матрицы
-ую строку матрицы  и умножить её на
и умножить её на  -ый столбец матрицы
-ый столбец матрицы  .
.




Поясним, как вычисляется, например элемент  . Для этого мы взяли вторую вектор-строку матрицы
. Для этого мы взяли вторую вектор-строку матрицы  и умножили ее скалярно на второй вектор-столбец матрицы
и умножили ее скалярно на второй вектор-столбец матрицы  :
: 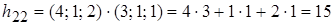 . Или для вычисления элемента
. Или для вычисления элемента  .
.
Определитель матрицы. Обратная матрица
Определитель (детерминант) матрицы – это число, (обозначаемое  , ∆,
, ∆,  ) которое сопоставляется квадратной матрице и может быть вычислено по ее элементам в соответствии со следующими правилами.
) которое сопоставляется квадратной матрице и может быть вычислено по ее элементам в соответствии со следующими правилами.
1) Детерминантом матрицы  порядка 1 называется единственный элемент этой матрицы:
порядка 1 называется единственный элемент этой матрицы:
 (2.1)
(2.1)
2) Для матрицы второго порядка мы имеем следующую формулу:
 (2.2)
(2.2)
из произведения элементов главной диагонали вычитаем произведение элементов побочной диагонали.
3) Для определителя третьего порядка применяют следующее правило:
1) Правило параллельного переноса.

 (2.3)
(2.3)

т.е. дописываем первые два столбца определителя матрицы. Далее суммируем произведения элементов главной диагонали и двух параллельных и вычитаем из них произведения элементов побочной диагонали и двух ей параллельных (над верхними элементами диагоналей проставлены соответствующие знаки).
2) Правило треугольника.

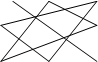

 (2.4)
(2.4)

4) Детерминантом матрицы

порядка  , при
, при  , называется число, определяемое формулой:
, называется число, определяемое формулой:
 (2.5)
(2.5)
или
 (2.6)
(2.6)
где  - определитель матрицы А, порядка
- определитель матрицы А, порядка  , полученный вычеркиванием из начальной матрицы i–ой строки и j–го столбца, и называемый минором элемента
, полученный вычеркиванием из начальной матрицы i–ой строки и j–го столбца, и называемый минором элемента  матрицы А. Формула (2.5) называется разложением определителя по строке, формула (2.6) – разложением по столбцу.
матрицы А. Формула (2.5) называется разложением определителя по строке, формула (2.6) – разложением по столбцу.
Алгебраическим дополнением элемента  матрицы А, называется произведение числа
матрицы А, называется произведение числа  на минор данного элемента и обозначается
на минор данного элемента и обозначается
 . (2.7)
. (2.7)
Свойства определителя:
1)(равноправность строк и столбцов) Определитель не изменится, если поменять местами строки со столбцами (т.е.  ).
).
2) Перестановка двух строк определителя (или двух столбцов) равносильна умножению определителя на 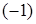 . Четное количество перестановок не меняет знака определителя.
. Четное количество перестановок не меняет знака определителя.
3)Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
4)Умножение всех элементов некоторой строки на число  равносильно умножению определителя на число
равносильно умножению определителя на число  .
.
5) Если все элементы некоторой строки (столбца) определителя равны нулю, то и определитель равен нулю.
6) Если все элементы некоторой строки (столбца) определителя пропорциональны какой-нибудь другой строке (столбцу), то определитель равен нулю. (Следует из свойств 3 и 4).
7)(Линейное свойство определителя) Если в определителе  -го порядка некоторая
-го порядка некоторая  -ая строка
-ая строка  является линейной комбинацией двух других строк
является линейной комбинацией двух других строк  и
и  с коэффициентами
с коэффициентами  и
и  , то
, то
 ,
,
где  - определитель у которого
- определитель у которого  -ая строка равна
-ая строка равна  , а
, а  - определитель у которого
- определитель у которого  -ая строка равна
-ая строка равна  , а все остальные строки те же, что и у основного определителя.
, а все остальные строки те же, что и у основного определителя.
Элементарными преобразованиями матрицы называются следующие преобразования:
1) умножение строки (столбца) на число отличное от нуля;
2) прибавление к одной строке (столбца) другую строку (столбец);
3) перестановка строк(столбцов).
8) Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) умноженные на произвольный множитель  , то величина определителя не изменится.
, то величина определителя не изменится.
9.)Треугольный определитель равен произведению диагональных элементов
 =
=  .
.
нижний треугольный верхний треугольный
определитель определитель
Матрица  - называется невырожденной (неособенной или несингулярной) матрицей если
- называется невырожденной (неособенной или несингулярной) матрицей если  . В противном случае
. В противном случае  - особенная (вырожденная или сингулярная).
- особенная (вырожденная или сингулярная).
Теорема: Всякая неособенная матрица имеет обратную матрицу, вычисляемую по формуле:
 . (2.8)
. (2.8)
Свойства обратной матрицы:
1.  ,
,
2.  ,
,
3.  если
если  - неособенные матрицы одного порядка.
- неособенные матрицы одного порядка.
5. Практикум
1. Для данной матрицы  вычислить определитель:
вычислить определитель:
1) методом параллельного переноса;
2) методом треугольника;
3) разложением по  -ой строке и по
-ой строке и по  -му столбцу;
-му столбцу;
4) вычислить, получив нулевые элементы в первом столбце используя элементарные преобразования со строками;
5) вычислить обратную матрицу  .
.
1)  ,
,  , 2)
, 2)  ,
,  ;
;
6. Решение типового задания
Для данной матрицы 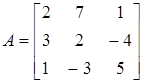 ,
,  вычислить определитель:
вычислить определитель:
1) методом параллельного переноса;
2) методом треугольника;
3) разложением по  -ой строке и по
-ой строке и по  -му столбцу;
-му столбцу;
4) вычислить, получив нулевые элементы в первом столбце используя элементарные преобразования со строками;
5) вычислить обратную матрицу  и проверить равенство
и проверить равенство  .
.
Решение.
1) Согласно правила параллельного переноса, допишем к нашему определителю две первые строки и сделаем действия согласно схеме (2.3)



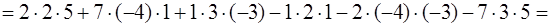
 .
.
2) согласно схеме (2.4) вычислим определитель методом треугольников:






 .
.
3) разложением по элементам 2-ой строки:

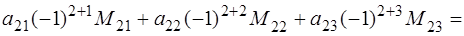
Выпишем миноры и вычислим их:
 ,
,  ,
,  .
.
Наше разложение по второй строке имеет вид:

 .
.
Разложением по элементам 3-его столбца:

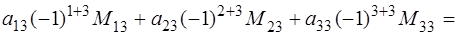
Аналогично предыдущего пункта записываем миноры, вычисляем их, получаем:

 .
.
4) Используя элементарные преобразования со строками, получим нулевые элементы в первом столбце. Для этого:
1) умножим третью строку на (-2) и прибавим к первой строке,
 ;
;
2) умножим третью строку на (-3) и прибавим ко второй строке.
 ;
;
Получили определитель эквивалентный исходному

Полученный определитель разложим по элементам первого столбца


5) Вычислить обратную  матрицу и проверить равенство
матрицу и проверить равенство  .
.
Решение:
Вычислим определитель матрицы:
 .
.
Т.к. определитель отличен от нуля, то матрица не является вырожденной и для нее определена обратная матрица. Для её нахождения протранспонируем матрицу  и вычислим её алгебраические дополнения по формулам (2.7)
и вычислим её алгебраические дополнения по формулам (2.7)
 ;
;
 ;
; 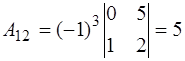 ;
;  ;
;  ;
;
 ;
;  ;
;
 ;
; 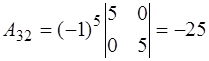 ;
;  .
.
Тогда обратная матрица согласно формуле (2.8) запишется в виде:
 .
.
Сделаем проверку и убедимся, что 

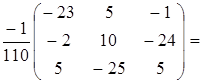
Вынесем числовой множитель и перемножим матрицы согласно формуле (1.4)

 .
.
Обратная матрица вычислена верно.
|
из
5.00
|
Обсуждение в статье: Определитель матрицы. Обратная матрица |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

