Неразрезную балку обычно решают методом сил

Рис. 1.8. Брус, нагруженный моментами.

При расчёте стержня на кручение нужно решить две основные задачи. Требуется определить напря­жения и найти угловые перемещения в зависимости от внешних моментов. Эти задачи решаются по- разному, смотря по тому, какой вид имеет поперечное сечение стержня. Наиболее просто можно полу­чить решение в случае кругового сечения, а также для широкого класса тонкостенных стержней.

Указанным правилом руководствуются при построении эпюр крутящих моментов (рис. 1.9).

Механизм деформирования стержня с круглым поперечным сечением можно представить себе в следующем виде: будем считать, что каждое поперечное сечение в результате действия внешних мо­ментов поворачивается в своей плоскости на некоторый угол как жёсткое целое. Этот угол поворота для различных сечений будет различным. Сказанное представляет собой гипотезу плоских сечений - пред­положение, оправдываемое общими правдоподобными соображениями о характере возникающих пере­мещений.

Рис. 1.9. Эпюры крутящих моментов.

Окончательным критерием пригодности любой гипотезы является опыт. Получив расчётную фор­мулу, нужно, прежде всœего, сопоставить результаты расчёта с экспериментом, и если между ними обна­руживается достаточно хорошее соответствие, гипотеза считается приемлемой.

В данном случае принятая гипотеза носит название гипотезы плоских сечений.

В поперечных сечениях стержня возникает постоянный крутящий момент

Двумя поперечными сечениями выделим из стержня элемент длиной dz, а из него в свою очередь двумя цилиндрическими поверхностями с радиусами ρ и ρ + dρ выделим элементарное кольцо.

Правое торцевое сечение кольца поворачивается при кручении относительно левого на угол dφ. Об­разующая цилиндра АВ поворачивается при этом на угол γ и занимает положение АВ^'. Отрезок ВВ^' ра­вен, с одной стороны, ρdφ, а с другой - γdz. Следовательно,

.

Угол γ представляет собой не что иное, как угол сдвига цилиндрической поверхности. Величина dφ/dz обозначается обычно через θ,

,

и принято называть относительным углом закручивания. Это — угол взаимного поворота двух сечений, отнесён­ный к расстоянию между ними. Величина θ аналогична относительному удлинœению при растяжении ∆l1. Вводя обозначение θ, получим

По закону Гука для сдига

,

где τ — касательные напряжения, возникающие в поперечном сечении бруса. Парные им напряжения воз­никают в продольных плоскостях - в осœевых сечениях.

Элементарные силы τdF приводятся к крутящему моменту

Интегрирование распространяется на всю площадь поперечного сечения F. Подставляя в подынте­гральную функцию напряжение τ из последней формулы, получим

Записанный в формуле интеграл представляет собой чисто геометрическую характеристику(см. п. 2), измеряется в см⁴ и носит название полярного момента инœерции сечения:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, получаем , или

.

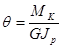Произведение GJ_p называют жесткостью стержня при кручении.

Через относительный угол закручивания θ легко определяется и величина взаимного угла поворота сечений φ. Имеем

откуда

,

где l - расстояние между сечениями, для которых определяется взаимный угол поворота φ.

В случае если крутящий момент по длинœе стержня не изменяется, М_к = М, и если жёсткость остаётся посто­янной, то

.

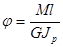Проведя преобразования, получим

.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, касательные напряжения в поперечном сечении распределœены вдоль радиуса по ли­нейному закону и имеют наибольшее значение в точках, наиболее удалённых от оси. При этом

Величина принято называть полярным моментом сопротивления и измеряется в см³. Окончательно имеем

Эти формулы являются основными расчётными формулами для кручения стержня с круговым по­перечным сечением. Οʜᴎ справедливы как для сплошного, так и для полого кругового сечения.

Определим теперь величины геометрических характеристик сечения J_p и W_p. В случае если стержень имеет сплошное круговое сечение, то

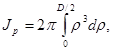
где D - диаметр сечения, или

В случае если же в стержне имеется внутренняя центральная полость диаметра d, то

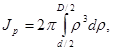
или

.

Соответственно этим выражениям определяем полярный момент сопротивления W_p:

для сплошного сечения

для кольцевого сечения (полый вал)

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, при заданном крутящем моменте угловые перемещения вала обратно пропорцио­нальны четвёртой степени диаметра. Что же касается наибольшего напряжения, то оно обратно пропор­ционально кубу диаметра D.

Касательные напряжения в поперечных сечениях бруса направлены в каждой точке перпендику­лярно к текущему радиусу р. Из условия парности следует, что точно такие же напряжения возникают и в продольных сечениях бруса. Наличие этих напряжений проявляется, к примеру, при испытании на кручение деревянных образцов.

 

 

2.

Изгиб — в сопротивлении материалов вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев, изменение кривизны/искривление срединной поверхности пластины или оболочки. Изгиб связан с возникновением в поперечных сечениях бруса или оболочки изгибающих моментов. Прямой изгиб балки возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.

Почти все задачи, решаемые в курсе сопротивления материалов, требуют построения эпюр внутренних силовых факторов. Самым универсальным методом построения эпюр является метод сечений. Однако подавляющее большинство эпюр являются настолько простыми, что применение метода сечений для их построения требует неоправданно больших затрат времени. В самом деле, однократное применение метода сечений нуждается по меньшей мере в одном рисунке и двух формулах. При этом даже для очень простой задачи (типа тех, что будут рассмотрены ниже) приходится делать три-четыре сечения. Известно, что при решении подобных задач львиная доля времени уходит не на обдумывание и вычисление, а на графические работы, то есть вычерчивание рисунков и запись формул. Метод сечений, являясь формальным, универсальным и мощным, удобен для решения или трудоемких задач на построение эпюр, или любых, но в начале, для накопления опыта. Однако для простых задач при наличии минимальных навыков он представляется излишне громоздким и поэтому требует слишком больших затрат. В то же время студентам, как правило, не объясняют упрощенные правила построения эпюр, а они, в свою очередь, не решают дополнительные задачи и не приобретают, таким образом, опыт быстрого получения ответа. Причем опыт этот не извлекается ни из книг, ни из лекций, а лишь накапливается путем самостоятельных упражнений. В результате задача, которая легко может быть решена в уме за полминуты, решается на трех листах бумаги в течение получаса. Это один из самых красноречивых примеров неоправданных затрат сил и главное – времени. Ниже будут даны некоторые советы по построению простейших эпюр вообще без использования метода сечений или, в крайнем случае, с его минимальным использованием. Подобные задачи требуют для решения очень небольшого времени (не более 40 секунд). Все задачи должны решаться исключительно в уме, без каких-либо дополнительных письменных построений или расчетов (кроме случаев, которые будут оговариваться особо).

Порядок построения эпюр методом сечений:

1. Определяются опорные реакции,
2. Определяется количество силовых участков бруса,
3. В пределах каждого участка брус делится на две части поперечным сечением,
4. Выбирается часть, к которой приложено меньше нагрузок,
5. Записываются необходимые выражения для внутренних силовых факторов,
6. Рассчитываются значения для характерных положений сечения,
7. Строятся эпюры.

 

Понятия о лин œейных и угловых перемещениях при изгиб е

Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). В случае если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, в связи с этим изогнутую ось бруса назы­вают упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, оста­ется в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол Θ.

Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонталь­ные перемещения сечений ничтожно малы и не учитываются. Рассмат­ривают вертикальные перемещения центра тяжести сечения, называе­мые прогибами (у). Максимальные прогибы обозначают f = у_таx. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

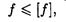
где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб. Иногда проверяется угол поворота сечения Θ < [Θ]. Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1*10^-3 рад.

Существует несколько методов определ œения перемещений сече ­ ний при изгибе . Один из них основан на дифференцировании урав ­ нения упругой линии , более рациональный способ — использование интегралов Мора . Метод Мора — универсальный способ определœения линœейны х и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

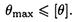
3

 

4.

расчет центрально сжатых стержней на основании условий устойчивости методом последовательных приближений

 

 

5.

1.Статистически неопределимые системы.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними.

Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.

На рис. 2.5, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А, т.е.

åx = 0, åy = 0. (2.16)

Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N₁ иN₂ в которой количество уравнений равно количеству неизвестных:

-N₁ - N₂ sin a = 0; -N₂ cos a - Р = 0.

Рис. 2.5

Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N₁, N₂ и N₃прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.

В общем случае под n-раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия наn единиц.

 

Неразрезную балку обычно решают методом сил

Сплошная балка, перекрывающая несколько пролетов, не прерывающаяся шарнирами, называется неразрезной.

Степень статической неопределимости неразрезной балки определяется по формуле:

 

n=C₀-3

 

Неразрезную балку обычно решают методом сил. В качестве основной системы выбирают балку с установленными над промежуточными опорами шарнирами. При таком выборе основной системы балка делится на отдельные однопролетные балки.

Если какой-либо конец балки имеет заделку (рис. 1), то в основной системе со стороны этого конца добавляется вместо заделки пролет длиной нуль. Консольные части балки (рис. 2) в основной системе отбрасываются, а их действия заменяются известными моментами.

 

Рисунок 1. Неразрезная балка

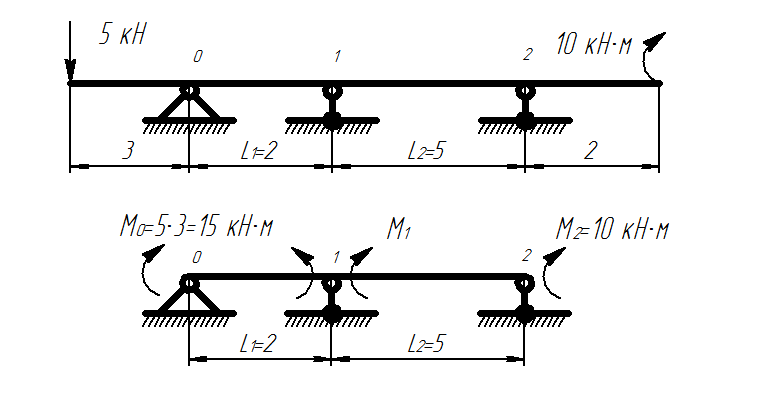
Рисунок 2. Неразрезная балка

 

Для каждой отдельной балки (участок между установленными шарнирами) строятся эпюры моментов от действия внешних сил, которые на ней расположены.

Каноническое уравнение метода сил для балки постоянного сечения принимает вид уравнения трех моментов и содержит не более трех неизвестных:

 

 

где M_n-1, M_n, M_n+1 – моменты на опорах n-1, n, n+1;

l_n, l_n+1 – длины соответствующих пролетов;

Bn^Ф, An+1^Ф – фиктивные опорные реакции.

 

 

где ω_n, ω_n+1 – площади эпюр моментов для простых балок;

a_n, b_n+1 – расстояние от центра тяжести соответствующей площади фигуры, ограниченной эпюрой моментов, до ближайшей левой опоры n или ближайшей правой опоры n+1.

 

 

Составляется столько уравнений трех моментов сколько лишних связей и, решив их, находятся неизвестные опорные моменты.

Строится эпюра опорных моментов М_оп – полученные значения опорных моментов откладываются от оси и соединяются прямыми в пределах пролетов.

Эпюра М для неразрезной балки равна сумме грузовых эпюр отдельных балок М_р и эпюры опорных моментов М_оп.

 

 

Метод сил

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

 

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

 

6.

Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции. Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механиз­мов также испытывают во время работы значительные динамические на­грузки от изменения величины и направления скоростей, то есть наличия ускорений^[1]. К динамическим нагрузкам относят и ударные нагрузки. При проектировании частей конструкции, находящихся под действием ударной или вибрационной нагрузки от станов, двигателей, молотов и т.д., производят расчёт на действие динамической нагрузки^[2]. Для устранения динамических нагрузок их снижают или ограничивают, например, при помощи электропривода, тормозных устройств и других механизмов^{[3] [4]}.

 

 

сопромате система называется статически определимой,если число неизвестных в ней равно числу полезных уравнений равновесия.

 

Для всякой пространственной системы сил (рис. 1.12, а) можно составить систему из 6-и уравнений равновесия и, решив ее, найти 6 неизвестных сил. Однако среди этих уравнений могут быть тождества, обращающиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил должно быть равно числу уравнений минус число тождеств.

 

Для произвольной плоской системы сил (рис. 1.12, б) можно составить 3 уравнения, не являющихся тождествами, например, сумму проекций всех сил на 2 любые оси и одну сумму моментов всех сил, относительно какой-либо точки.

 

Для плоской системы сходящихся сил (рис.1.12, в) можно составить лишь 2 уравнения, не являющихся тождествами. Сумма моментов всех сил относительно точки их пересечения тождественно равна нулю. Из 2-х уравнений (любых) можно определить лишь 2 неизвестные силы.

 

Для плоской системы параллельных сил (рис.1.12, г) бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Соответственно из 2-х любых уравнений равновесия можно найти лишь 2 неизвестные силы.

 

Для системы коллинеарных сил (действующих вдоль одной прямой линии) (рис. 1.12, д) можно составить лишь одно полезное уравнение — сумму проекций всех сил на эту прямую, которая равна просто сумме сил.

 

 

Ударные нагрузки

Ударные нагрузки

Это нагрузки, возникающие в момент соприкосновения перемещающегося объекта с поверхностью исследуемой конструкции (вдоль или поперек рассматриваемой оси элемента).

Однако и это еще не все варианты классификации нагрузок. По площади приложения нагрузки делятся на сосредоточенные и распределенные.

 

7.

Таким образом, уравновешиванию подлежат силы инерции, развиваемые массой т^, сосредоточенной в точке А, и общей массой тв, сосредоточенной в точке В и равной тв = т„ + /Яш> где тп — масса ползуна (поршня). Сила инерции РА = —т^аА легко может быть уравновешена противовесом, расположенным на кривошипе ОА по другую сторону от оси вращения. Уравновешивание силы инерции Рв, развиваемой массой тв, представляет значительную трудность, так как ее величина изменяется по сложной зависимости от угла поворота кривошипа <р. Величина этой силы составляет Рв = —твав, где ав — ускорение ползуна, которое приближенно определяется по равенству

Карбидные покрытия можно также наносить напылением или намазыванием на поверхность детали полужидкой массы, содержащей требуемый для покрытия порошок карбида. Нанесенная паста подвергается сушке и припеканию в вакууме. При осуществлении этого метода значительную трудность представляет получение хорошего сцепления покрытия с основой, кроме того, покрытие обладает значительной пористостью. Для получения покрытий наиболее непроницаемых и по возможности с минимальным количеством пузырьков разработана технология спекания покрытий по ступенчатому режиму [5]. Таким методом наносятся на вольфрам покрытия из циркона и стекла. Обязательным этапом перед нанесением покрытия является дегазация вольфрамовых образцов.

Необходимо отметить, что оценка развития дефекта во времени представляет значительную трудность, методически не отработана и сложна при использовании серийной аппаратуры, поэтому эксплуатация осей с дефектами — необоснованный риск. Замена дефектных новыми осями позволила бы дефектоскопистам повысить безопасность, проанализировать повреждения, уточнить методику контроля.

Значительную трудность в расшифровке характера разрушения представляют изломы высокопрочных металлов и сплавов. Из-за высокой чувствительности к трещине усталостная зона в изломах этих материалов занимает относительно малую зону, что также затрудняет анализ.

Решение прямой задачи теории упругости представляет значительную трудность. Тем не менее на сегодня известно решение ряда важных классов задач; к числу их относятся: плоская задача, Ьсесимметричная задача, задача для слоя, полупространства и другие. Во всех упомянутых классах задач, в каждом конкретном случае остается лишь вычислительная работа (правда, порою далеко не простая), принципиальные же сложности проблем преодолены.

Механические воздействия на аппаратуру. Аппаратура и приборы, установленные на объекты, подвергающиеся в условиях эксплуатации воздействию знакопеременных сил, испытывают вибрационные нагрузки, могущие привести к их неисправности и поломке. Действие вибрационных нагрузок сказывается также при транспортировании аппаратуры, при работе мощных механизмов рядом с ней. Причины возникновения вибрации различные, например, в механизмах вибрация может быть вызвана периодическими силами, возникающими при движении с ускорениями неуравновешенных масс вследствие периодических толчков, из-за неодинаковой жесткости различных элементов конструкций. Около 70—80 % отказов изделий в машиностроении являются результатом действия вибрации. Интенсивность воздействия вибрации на изделие определяется не только амплитудой колебаний, но и максимальным ускорением. Наибольшую опасность для аппаратуры, находящейся под воздействием вибрации, создают резонансные эффекты, когда частота вибрации близка к собственным частотам колебаний элементов конструкции. Значительную трудность в распознавании представляют параметрические резонансы элементов аппаратуры, борьба с которыми затруднена в связи с тем, что параметрические колебания происходят в низкочастотных и высокочастотных диапазонах частот.