 |
Главная |
Трение гибкой нити о цилиндрическую поверхность.
|
из
5.00
|
Трение скольжения
До сих пор было рассмотрено равновесие преимущественно идеальных механических систем в предположении, что поверхности соприкасающихся тел являются абсолютно гладкими и что всякое трение между соприкасающимися телами отсутствует, а сами тела – абсолютно твердыми. Такое рассмотрение лишь приближенно соответствует действительности.
Как уже говорилось, связи накладывают ограничения на перемещения материальных точек. Эти ограничения можно представить в виде некоторых поверхностей, на которых вынуждена оставаться соответствующая материальная точка (или твердое тело). В природе свободному скольжению всегда препятствуют некоторые силы, которые называют силами трения.
Силы трения существенно отличаются от всех других сил. Они возникают в тех случаях, когда активные силы способны создать движение соприкасающихся тел. Наука, занимающаяся трением, называется триботехникой.
Величины этих сил трения зависят от целого ряда различных факторов. Пусть, например, тело находится на горизонтальной плоскости, и на него действует горизонтальная сила  , вес тела
, вес тела  , реакция связи
, реакция связи  (рис. 11.1а).
(рис. 11.1а).
| а | 
| б | 
|
| Рис.11.1 | |||
Из опыта известно, что тело начнет двигаться горизонтально лишь тогда, когда величина силы  станет достаточно большой. Состояние покоя тела при отличной от нуля величине силы
станет достаточно большой. Состояние покоя тела при отличной от нуля величине силы  свидетельствует о том, что сила
свидетельствует о том, что сила  уравновешивается другой силой
уравновешивается другой силой  , называемой силой трения. Сила трения
, называемой силой трения. Сила трения 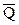 уравновешивает силу
уравновешивает силу  лишь до тех пор, пока величина силы
лишь до тех пор, пока величина силы  не превзойдет некоторого определенного предела, после чего тело начнет двигаться. В реальных задачах мы имеем дело не с идеальными связями. Поэтому полная реакция всегда может быть представлена в виде векторной суммы нормальной реакции
не превзойдет некоторого определенного предела, после чего тело начнет двигаться. В реальных задачах мы имеем дело не с идеальными связями. Поэтому полная реакция всегда может быть представлена в виде векторной суммы нормальной реакции  и силы трения и составит угол φ с нормалью (рис.11.1б).
и силы трения и составит угол φ с нормалью (рис.11.1б).
Закон Амонтона-Кулона
Законы трения изучал французский физик Гильом Амонтон (1663-1705), установивший независимость величины трения от величины поверхностей соприкосновения. В более законченной форме законы трения были сформулированы французским инженером Шарлем Кулоном (1736-1806). Установленные Г. Амонтоном и Ш. Кулоном законы трения используются в технике и по настоящее время. Мы же ограничимся лишь упрощенной трактовкой законов Амонтона-Кулона, предполагая, что сила трения по величине пропорциональна силе нормального давления соприкасающихся тел, т.е.
Fтр=kN.
| Коэффициент пропорциональности k определяется опытным путем и зависит от многих параметров, например, температуры, относительных скоростей соприкасающихся точек (рис.11.2) и т.д. |  Рис.11.2
Рис.11.2
|
Максимальное значение k принимает в момент нарушения относительного покоя. Коэффициент f = kmax называют коэффициентом трения.
Угол и конус трения
Угол 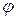 , образованный нормалью к поверхности связи и линией действия равнодействующих сил – нормального давления и максимальной величины силы трения, - называется углом трения (рис.11.3,а). Угол трения
, образованный нормалью к поверхности связи и линией действия равнодействующих сил – нормального давления и максимальной величины силы трения, - называется углом трения (рис.11.3,а). Угол трения 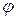 связан с коэффициентом трения соотношением
связан с коэффициентом трения соотношением


 Полная реакция, действующая на точку со стороны поверхности связи, состоит из нормальной реакции и силы трения и лежит всегда внутри угла трения. Если в точке соприкосновения тела с поверхностью построить конус, ось которого направлена по нормали к поверхности связи, а угол при вершине равен
Полная реакция, действующая на точку со стороны поверхности связи, состоит из нормальной реакции и силы трения и лежит всегда внутри угла трения. Если в точке соприкосновения тела с поверхностью построить конус, ось которого направлена по нормали к поверхности связи, а угол при вершине равен  , то реакция связи в данной точке всегда будет находиться внутри этого конуса, который называется конусом трения (рис.11.3,б). Шероховатость
, то реакция связи в данной точке всегда будет находиться внутри этого конуса, который называется конусом трения (рис.11.3,б). Шероховатость
| а | 
| б | 
|
| Рис.11.3 | |||
по разным направлениям может оказаться неодинаковой. Тогда для разных направлений коэффициент трения также будет различным, а конус трения вообще не будет прямым круговым конусом.
Рассмотрим условия равновесия материальной точки на шероховатой поверхности. На точку действует активная сила  , образующая угол
, образующая угол  с нормалью касательной плоскости к поверхности (рис.11.3б).
с нормалью касательной плоскости к поверхности (рис.11.3б).
Если  , то линия действия силы
, то линия действия силы  будет лежать внутри конуса трения и действие на точку силы
будет лежать внутри конуса трения и действие на точку силы  будет всегда уравновешиваться действием силы реакции, лежащей внутри конуса трения, как бы велика ни была сила.
будет всегда уравновешиваться действием силы реакции, лежащей внутри конуса трения, как бы велика ни была сила.
Если  , то линия действия
, то линия действия 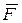 уже не будет находиться внутри конуса трения и сила
уже не будет находиться внутри конуса трения и сила 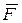 не может быть уравновешена силой реакции. В этом случае точка начнет двигаться под действием силы
не может быть уравновешена силой реакции. В этом случае точка начнет двигаться под действием силы 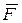 , как бы ни была мала эта сила по величине.
, как бы ни была мала эта сила по величине.
Рассмотрим равновесие тяжелой материальной точки, которая
 Рис.11.4
Рис.11.4
| находится на шероховатой наклонной плоскости, составляющей угол  с горизонтом (рис.11.4), угол трения равен с горизонтом (рис.11.4), угол трения равен 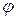 .
Точка будет находиться в равновесии лишь тогда, когда линия действия силы тяжести будет проходить внутри .
Точка будет находиться в равновесии лишь тогда, когда линия действия силы тяжести будет проходить внутри
|
угла трения, т.е. при выполнении неравенства  .
.
Следствия:
Равнодействующая активных сил, проходящая внутри конуса трения, не может вызвать движения тела, как бы велика она ни была.
Как бы ни была мала равнодействующая активных сил, не лежащая внутри конуса трения, она не может быть уравновешена силами трения и сообщает телу движение.
Пример1. Однородный стержень АВ длиной L опирается одним концом на гладкую вертикальную стену, а другим В – на шероховатую вертикальную стену (рис.11.5). Расстояние между стенами h<L. Определить коэффициент трения стены f, при котором возможно равновесие стержня.
Решение. Рассмотрим случай, когда точка А расположена выше точки В стержня. На стержень действует сила тяжести  , приложенная посередине, нормальная реакция гладкой стены NA и реакция шероховатой стены RB, которую разложим на нормальную реакцию NB и силу трения
, приложенная посередине, нормальная реакция гладкой стены NA и реакция шероховатой стены RB, которую разложим на нормальную реакцию NB и силу трения  FBтр .
FBтр .

| Составим условия равновесия плоской системы сил:

|
| Рис.11.5 |
К этим уравнениям следует добавить неравенство для сил трения

Из уравнений равновесия находим 
Из геометрических условий задачи имеем: 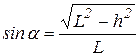 .
.
Для силы трения  имеем следующие уравнение и неравенство:
имеем следующие уравнение и неравенство:
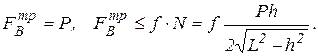
Исключая из них силу трения  , после сокращения на Р получаем:
, после сокращения на Р получаем:  .
.
Искомое условие для коэффициента трения f при равновесии стержня
принимает вид 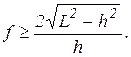
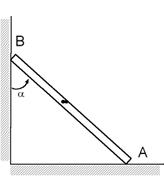
Пример 2. Лестница опирается концами А и В на горизонтальный пол и вертикальную стену (рис. 11.6). Пренебрегая весом лестницы, определить, при каких положениях стоящего на ней человека система остается в равновесии. Углы трения  А и
А и  В в точках А и В известны.
В в точках А и В известны.
| a |

| б |
| Рис. 11.6 |
Решение. Решим задачу графически. На лестницу действует сила тяжести Р, равная весу человека, реакции RA и RB в точках А и В, которые могут иметь любые направления внутри углов трения. При равновесии сил 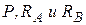 должны пересекаться в одной точке. Но реакции R А и R B могут пересекаться где угодно внутри заштрихованной на чертеже площади (рис. 11.6). Следовательно, при равновесии линия действия силы Р должна пересекать эту площадь.
должны пересекаться в одной точке. Но реакции R А и R B могут пересекаться где угодно внутри заштрихованной на чертеже площади (рис. 11.6). Следовательно, при равновесии линия действия силы Р должна пересекать эту площадь.
При том положении лестницы, которое показано на рисунке, человек может подняться только до точки Д. Чтобы человек мог дойти до верхнего конца лестницы, угол  , который она образует с вертикалью, должен быть не больше угла трения
, который она образует с вертикалью, должен быть не больше угла трения  А (от трения в точке В этот результат не зависит).
А (от трения в точке В этот результат не зависит).
При отсутствии трения реакции R А и R B будут перпендикулярны поверхностям и пересекутся в точке О . Равновесие будет возможно только тогда, когда человек стоит в точке А лестницы.
Трение гибкой нити о цилиндрическую поверхность.
Рассмотрим нить, касающуюся поверхности кривого цилиндра вдоль дуги ADEB с центральным углом α (рис.11.6а). Коэффициент трения нити о цилиндр равен fo. К одному концу нити приложена сила P. Найдем, какую наименьшую силу  надо приложить к другому концу, чтобы сохранить равновесие.
надо приложить к другому концу, чтобы сохранить равновесие.
| а | 
| б |

|
| Рис.11.6 | |||
Для этого рассмотрим равновесие элемента нити DE длины  , где R – радиус цилиндра. На него действуют приложенные в точках D и Е натяжение нити
, где R – радиус цилиндра. На него действуют приложенные в точках D и Е натяжение нити  и
и  , нормальная реакция
, нормальная реакция  и сила трения
и сила трения  . Составляя условия равновесия в проекциях на касательную
. Составляя условия равновесия в проекциях на касательную  и нормаль
и нормаль  и считая
и считая 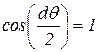 ,
,  , будем иметь (с точностью до членов второго порядка малости) (рис.11.6б):
, будем иметь (с точностью до членов второго порядка малости) (рис.11.6б):

Но так как рассматриваемое положение равновесия является предельным, то dFтр = f0dN. Подставляя сюда значения dF и dN, полученные выше, получим
 .
.
Так как напряжение нити в точках А и В равно соответственно Р и Q, то, разделяя в полученном уравнении переменные и беря от обеих частей определенные интегралы в соответствующих пределах, получим:
 , или
, или  ,
,
откуда

Полученная формула (формула Эйлера) показывает, что уравновешивающая сила Q не зависит от радиуса цилиндра и при данном f0 быстро убывает с увеличением  .
.
Трение качения
Трением качения называется сопротивление, возникающее при качении одного тела по другому.
| а |

| б | 
|
| Рис.11.7 | |||
Трение качения возникает оттого, что при движении деформации подвергается как поверхность, так и колесо. Колесо несколько сплющивается, т.е. его нельзя считать абсолютно твердым – расстояние между двумя точками при движении перестает быть постоянным. Поэтому поверхность катящегося тела и плоскость, по которой тело катится, несколько деформируются вследствие давления тела на плоскость.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием веса катка P и горизонтальной силы Q, приложенной в его центре (рис.11.7а). В точке соприкосновения катка с плоскостью возникает нормальная реакция N этой плоскости, равная весу катка P, и сила трения Fтр, препятствующая скольжению катка по плоскости и равная по модулю силе Q, но направленная в противоположную сторону.
Однако если бы сопротивление неподвижной плоскости сводилось только к силам N и Fтр, то каток не мог бы быть в равновесии, так как пара (Q,Fтр) оставалась бы, очевидно, неуравновешенной. Поэтому необходимо допустить, что результирующая реакция неподвижной плоскости приводится не только к силам N и Fтр, но еще и к некоторой паре, которая уравновешивает пару (Q,Fтр), т.е к паре (  ) рис.11.7.
) рис.11.7.
Эта пара, препятствующая качению катка, называется парой качения. Кулон опытным путем нашел, что момент этой пары не может превышать некоторого определенного в условиях данного опыта максимального значения; это максимальное значение момента пары трения качения не зависит от радиуса катка и прямо пропорционально нормальному давлению катка на плоскость или, что то же, нормальной реакции N.
Таким образом, если обозначим абсолютную величину этого максимального момента пары трения качения через Мmax, то Мmax = fkN, где fk – коэффициент пропорциональности, называемый коэффициентом трения качения. Этот коэффициент выражается в линейных единицах. Значение коэффициента трения качения определяется опытным путем и зависит от материала катка и опорной поверхности.
Рассмотрим общий случай равновесия катка. Пусть к катку приложена горизонтальная сила Q в точке В, так что АВ = h (рис.11.7б), и пусть каток находится в покое. В точке А к катку приложены сила трения скольжения 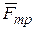 и нормальная реакция N опорной плоскости, направленная вертикально вверх и отстоящая от линии действия веса Р на величину d.
и нормальная реакция N опорной плоскости, направленная вертикально вверх и отстоящая от линии действия веса Р на величину d.
Напишем уравнения равновесия сил, приложенных к катку:

Максимальное значение модуля силы Fтр есть
Fmax = f N = f P ,
где f – коэффициент трения скольжения; следовательно,
 .
.
Кроме того, величина Nd = М есть момент пары трения качения; эта величина не может быть больше fkN; следовательно,  , а поэтому
, а поэтому
 , или
, или  ,
,
т.е.
 и
и  .
.
Итак, при равновесии катка сила Q должна удовлетворять условиям
 и
и 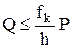 .
.
Если эти условия выполнены, то не произойдет ни скольжения, ни качения катка.
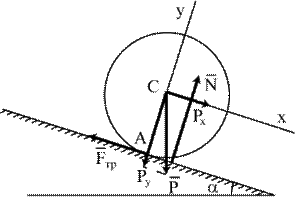
Пример 3. Определить, при каких значениях угла a (рис.11.8) цилиндр радиуса R, лежащий на наклонной плоскости, остается в покое, если коэффициент качения равен fk.
Решение. Рассмотрим предельное положение равновесия, когда  . Разлагая силы Р на составляющие Рх и Ру, запишем уравнения равновесия:
. Разлагая силы Р на составляющие Рх и Ру, запишем уравнения равновесия:
| 
|
| Рис.11.8 |
При уменьшении fk до нуля величина  также убывает до нуля. Отсюда заключаем, что равновесие сохранится при любом
также убывает до нуля. Отсюда заключаем, что равновесие сохранится при любом  .
.
Полученным результатом можно пользоваться для определения коэффициента fk, находя угол  из опыта.
из опыта.
Библиографический список
1. Тарг С. М. Курс теоретической механики. - М.: Высш. шк., 1995. - 416 с.
2. Никитин Н. Н. Курс теоретической механики. - М.: Высш. шк., 1990. -606 с.
3. Сопротивление материалов с основами теории упругости и пластичности: Учебник./Под ред. С. Г. Варданяна. - М.: Изд-во "АСВ", 1995. - 568 с.
4. Александров А. В., Потапов В. Д., Державин Б. П., Сопротивление материалов: Учеб. для вузов/ А. В. Александров, В. Д. Потапов, Б. П. Державин. - М.: Высш. шк., 1995. - 560 с.
5. Строительная механика. изд. 7-е, перераб. и доп: Учеб. для вузов. / Под ред. А. В. Даркова - М.: Высш. шк., 1976. - 600 с.
6. Богомаз И.В. Теоретическая механика. Статика: Тексты лекций. - Красноярск: КрасГАСА, 1999. 85с.
|
из
5.00
|
Обсуждение в статье: Трение гибкой нити о цилиндрическую поверхность. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

