 |
Главная |
Экспериментальное определение моментов инерции
|
из
5.00
|
Рассмотрим определение момента инерции тела способом крутильных колебаний. Тело подвешивают на упругом стержне или струне так, чтобы центр масс тела лежал на продолжении оси стержня (рис. 4.4 а). Закрутив стержень, жестко связанный с телом, на малый угол  , измеряют период колебания системы.
, измеряют период колебания системы.
|
Рис. 4.4 |
Так как при малом угле закручивания момент упругих сил пропорционален этому углу, то дифференциальное уравнение крутильных колебаний системы имеет вид
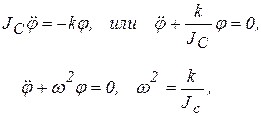
где k – постоянный коэффициент, характеризующий упругие свойства струны (стержня).
Частота и период колебаний, очевидно, будут
 . (4.9)
. (4.9)
Затем на тот же стержень подвешивают тело (например, диск), момент инерции которого относительно оси ОС известен и равен  , и измеряют период колебаний
, и измеряют период колебаний 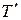 в этом случае.
в этом случае.
Период колебаний 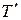 определяется аналогично (4.9):
определяется аналогично (4.9):
 . (4.10)
. (4.10)
Исключая в равенстве (4.9) и (4.10) неизвестный коэффициент k, получим формулу для определения момента инерции
 .
.
Плоское движение твердого тела
При плоском движении все точки твердого тела движутся в параллельных плоскостях. Поэтому достаточно рассмотреть движение какого-либо сечения тела в одной плоскости (рис. 4.1).
В соответствии с (4.1) имеем


Cогласно (3.16), кинетический момент твердого тела 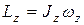 , тогда дифференциальный закон плоско – параллельного движения примет вид
, тогда дифференциальный закон плоско – параллельного движения примет вид
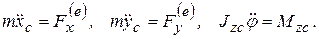 (4.11)
(4.11)
где m – масса тела,  - момент инерции твердого тела относительно оси вращения,
- момент инерции твердого тела относительно оси вращения,  главный момент внешних сил относительно оси вращения.
главный момент внешних сил относительно оси вращения.
Если тело совершает несвободное движение, то в число внешних сил следует включить реакции связей.
Скатывание цилиндра с наклонной плоскости
|
Рис. 4.5 |
Будем считать, что скатывание цилиндра радиусом R происходит без скольжения. Силы, действующие на цилиндр, указаны на рис. 4.5. Сила Т – сила сцепления, которая обеспечивает скатывание цилиндра. Ось х удобно направить вдоль наклонной плоскости. Напишем законы движения, имея в виду, что через точку С проходит мгновенная ось вращения. Уравнения (4.11) имеют вид
 ,
,  , (4.12)
, (4.12)
где  ; отсчет направлений вращения выбран так, чтобы угловая скорость
; отсчет направлений вращения выбран так, чтобы угловая скорость  (
(  ) увеличивалась при скатывании цилиндра.
) увеличивалась при скатывании цилиндра.
Вычисляя Т из второго уравнения (4.12) и подставляя в первое, учитывая, что  , получим
, получим
 ,
,
или
 . (4.13)
. (4.13)
Таким образом, центр масс цилиндра движется с постоянным ускорением  .
.
Маятник Максвелла
|
Рис. 4.6 |
Маятник Максвелла представляет собой диск, подвешенный на нерастяжимой нити. Нить конечной длины намотана на ось диска и закреплена на оси (рис. 4.6). Уравнения движения маятника имеют вид
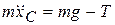 ,
, 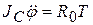 , (4.14)
, (4.14)
где  - момент инерции всего диска относительно оси, проходящей через центр масс;
- момент инерции всего диска относительно оси, проходящей через центр масс;  - радиус оси диска, на которую намотана нить; Т – сила натяжения.
- радиус оси диска, на которую намотана нить; Т – сила натяжения.
Структура уравнений маятника Максвелла полностью аналогична структуре уравнений цилиндра, скатывающегося с наклонной плоскости (уравнения 4.12) и решаются аналогично.
Получаем из (4.14)
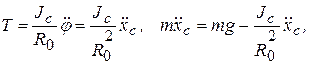
откуда
 (4.15)
(4.15)
Проследим динамику движения маятника. Ускорение диска всегда постоянно и направлено вниз. Его числовое значение тем меньше, чем больше момент инерции  . При достаточно большом моменте инерции
. При достаточно большом моменте инерции  диск будет иметь малое ускорение. В пределе
диск будет иметь малое ускорение. В пределе  ,
, 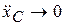 , а
, а 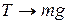 ; так и должно быть, потому что диск просто висит на нити без движения. При
; так и должно быть, потому что диск просто висит на нити без движения. При  сила натяжения нити
сила натяжения нити  . В этом случае диск свободно падает, и поэтому нить не испытывает никакого натяжения. Уравнения (4.14) и решение (4.15) не описывают поведение маятника в нижней «мертвой» точке. В этом положении центр масс диска испытывает большое ускорение. По третьему закону Ньютона, это приводит к большому натяжению нити. Если нить недостаточно прочна, то она может в этот момент порваться.
. В этом случае диск свободно падает, и поэтому нить не испытывает никакого натяжения. Уравнения (4.14) и решение (4.15) не описывают поведение маятника в нижней «мертвой» точке. В этом положении центр масс диска испытывает большое ускорение. По третьему закону Ньютона, это приводит к большому натяжению нити. Если нить недостаточно прочна, то она может в этот момент порваться.
|
Рис. 4.7 |
Рассмотрим еще один пример плоского движения тела.
Пример. На двух нерастяжимых невесомых нитях одинаковой длины подвешен в точке О однородный стержень АВ массой m и длиной 2 L (рис.4.7). Нити со стержнем образуют углы  . В некоторый момент времени нить ОВ обрывается. Найти натяжение Т нити ОА непосредственно после момента обрыва.
. В некоторый момент времени нить ОВ обрывается. Найти натяжение Т нити ОА непосредственно после момента обрыва.
Решение. Движение стержня после разрыва нити плоское. В момент разрыва ускорение центра находится по теореме об ускорениях при плоском движении. За полюс выберем точку А. Вычислим ускорение центра масс стержня АВ, т.е. ускорение точки С:
 , (4.16)
, (4.16)
здесь  - ускорение полюса А,
- ускорение полюса А, 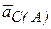 - ускорение центра масс при его вращении относительно полюса А. Поскольку точка А может двигаться только по окружности радиуса ОА, а ее скорость в момент обрыва нити равна нулю, то
- ускорение центра масс при его вращении относительно полюса А. Поскольку точка А может двигаться только по окружности радиуса ОА, а ее скорость в момент обрыва нити равна нулю, то 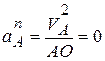 . Проекцию ускорения точки А по касательной обозначим
. Проекцию ускорения точки А по касательной обозначим  .
.
|
Рис. 4.8 |
Обозначим модуль углового ускорения стержня через 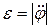 , а модуль угловой скорости через
, а модуль угловой скорости через  (начальный момент времени равен нулю). Тогда
(начальный момент времени равен нулю). Тогда  и направлена вдоль стержня от точки С к точке А;
и направлена вдоль стержня от точки С к точке А; 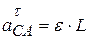 и направлена перпендикулярно стержню в точке А (рис. 4.8).
и направлена перпендикулярно стержню в точке А (рис. 4.8).
Выберем систему координат x С y, как показано на рис. 4.8. Тогда ускорение точки  имеет следующие проекции на эти оси:
имеет следующие проекции на эти оси:
 (4.17)
(4.17)
Поскольку 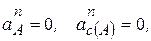 закон плоского движения (4.11) с учетом (4.17) запишется
закон плоского движения (4.11) с учетом (4.17) запишется
 (4.18)
(4.18)
где учтено, что момент инерции стержня относительно его центра 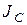 , равен
, равен  .
.
Из третьего уравнения (4.18) выразим  и подставим в первое уравнение, получим
и подставим в первое уравнение, получим
 .
.
Отсюда находим
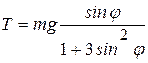 .
.
|
из
5.00
|
Обсуждение в статье: Экспериментальное определение моментов инерции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы






