Методические указания.

Лабораторная работа №3

Вычисление функций с использованием их разложения в степенной ряд

Цель работы.

Практика в организации итерационных и арифметических циклов.

 

Теоретические сведения.

 

       Действительная функция f(x) называется аналитической в точке e, если в некоторой окрестности ½x-e½<R этой точки функция разлагается в степенной ряд (ряд Тейлора):

(1)

При e=0 получаем ряд Маклорена:

                              (2)

Разность                                                    (3)

называется остаточным членом и представляет собой ошибку при замене функции f(x) полиномом Тейлора.

       Для ряда Маклорена

 где 0<q<1.                                                                 (4)

       Таким образом, вычисление значения функции можно свести к вычислению суммы числового ряда

а₁+а₂+ . . . +a_n+ . . . .                                                                              (5)

       Известно, что числовой ряд называется сходящимся, если существует предел последовательности его частных сумм:

       ,                                                                                 (6)

где S_n= а₁+а₂+ . . . +a_n+ . . . .

       Число S называется суммой ряда.

       Из формулы (13) получаем S=S_n+R_n ,

где R_n - остаток ряда, причем R®0 при n®¥.

Для нахождения суммы S сходящегося ряда (5) с заданной точностью e нужно выбрать число слагаемых n столь большим, чтобы имело место неравенство

½R_n½<e.

       Тогда частная сумма S_n приближенно может быть принята за точную сумму S ряда (5).

       Приближенно n выбрать так, чтобы имело место неравенство

|S_n+1-S_n|<e или a_n<e.

       Задача сводится к замене функции степенным рядом и нахождению суммы некоторого количества слагаемых при различных параметрах суммирования х . Каждое слагаемое суммы зависит от параметра х и номера n, определяющего место этого слагаемого в сумме.

       Обычно формула общего члена суммы принадлежит одному из следующих трех типов:

а) ;        ;     ;

 

б) ; ;         ;

 

в) ;   ;      .

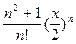       В случае а) для вычисления члена суммы а_n целесообразно использовать рекуррентные соотношения, т. е. выражать последующий член суммы через предыдущий: a_n+1=y(x, n)a_n. Это позволит существенно сократить объем вычислительной работы. Кроме того, вычисление члена суммы по общей формуле в ряде случаев невозможно (например из-за наличия n!).

       В случае б) применение рекуррентных соотношений нецелесообразно. Вычисления будут наиболее эффективными, если каждый член суммы вычислять по общей формуле a_n=f(x, n).

       В случае в) член суммы целесообразно представить в виде двух сомножителей, один из которых вычисляется по рекуррентному соотношению, а другой непосредственно           a_n=f(x, n)*с_n(x,n), где с_n=c_n-1y(x,n).

           

Постановка задачи.

Для х изменяющегося от a до b с шагом (b-a)/k, где (k=10), вычислить функцию f(x), используя ее разложение в степенной ряд в двух случаях:

а) для заданного n;

б) для заданной точности e (e=0.0001).

Для сравнения найти точное значение функции.

 

Методические указания.

       Алгоритм решения задачи сводится к трем циклам, причем два из них вложены в третий. Внутренние циклы суммируют слагаемые при фиксированном параметре x, один (арифметический для заданного n), другой (итерационный для заданной точности e. При организации этих циклов следует обратить внимание на правильный выбор формулы для вычисления элемента ряда a_n и правильное присвоение начальных значений переменным цикла. Внешний цикл организует изменение параметра х.

       Результаты расчетов отпечатать в следующем виде:

 

 

                   Вычисление функции

X=...... SN=......     SE=.....       Y=......

X=...... SN=......     SE=.....       Y=......

                   ..........

X=...... SN=......     SE=.....       Y=......

Здесь X- значение параметра; SN- значение суммы для заданного n; SE- значение суммы для заданной точности; Y-точное значение функции.

 

Варианты

 

№	функция	Диапазон Изменения аргумента	n	сумма
1		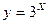	10
2		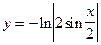	40
3			10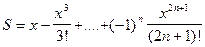
4			10
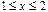
5			15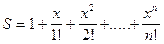
6			25
7			10
8		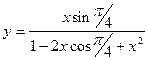	40
9			3
10			20
11			10
12			35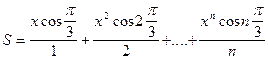
13			10
14			20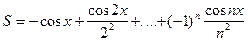
15			30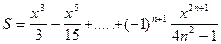
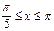
16			40
17			10
18		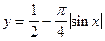	50
19			20
20			30
21			40
22			35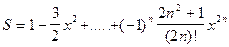
23			15
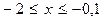
24			40
25		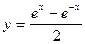	20
26			25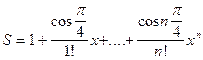
27			10
28		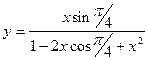	40
29			3
30			20

 

3.5. Содержание отчета:

1. Постановка задачи (общая и конкретного варианта).

2. Алгоритм программы.

3. Текст программы.

4. Результаты работы программы (10 точек, для каждой 3 результата: y, SN, SE).