Параллельность прямой и плоскости

Аксиомы стереометрии и их простейшие следствия

№1 Изобразите прямую a пересекающую плоскость α

№2 Изобразите две пересекающиеся плоскости α и β

№3 Вставьте пропуски

А1: Через любые три точка, ________________________________________, проходит плоскость, и притом _____________________________________.

А2: Если две точки прямой лежат в плоскости, то _____________________________________________ лежат в этой плоскости.

А3: Если две плоскости имеют общую точку, то они имеют _____________

___________________, на которой лежат _____________________________

____________ этих плоскостей.

С1: Через прямую и ___________________________________ проходит плоскость и притом только одна.

С2: Через _________ пересекающиеся прямые проходит плоскость и _______________.

№ 4 Проведите плоскость через прямую m (см. рис.). Сколько таких плоскостей можно провести?

№ 5 Дан куб А…D₁ (см. рис.). Проведите плоскость через его вершины А, D и точку F – центр грани A₁B₁C₁D₁.

№ 6 В треугольной пирамиде ABCD (см. рис.) проведите плоскость через вершины A, B и точку P – середину ребра DC. Запишите, по каким прямым пересекается эта плоскость с плоскостями, в которых лежат грани пирамиды.

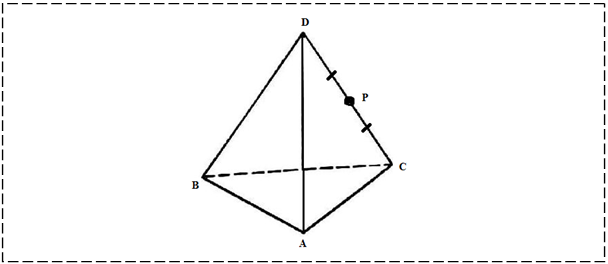
№ 7 На рисунке изображен тетраэдр ABCD. На его боковых ребрах DA, DB и DC взяты соотвственно точки E, F и G. Установите, пересекается ли отрезок BC с плоскостью EFG.

Параллельность прямых в пространстве. Скрещивающиеся прямые

№ 1 Вставьте пропущенные слова в предложениях

Опр1: Две прямые в пространстве называются параллельными, если они __________________ и _____________________________.

Т1: Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и ___________________________.

Л1: Если одна из двух ______________ прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

№2 Вставьте пропущенные слова в предложениях

Опр2: Две прямые называются скрещивающимися, если они __________________________________.

Т2: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, _______________________________, то эти прямы называются скрещивающимися.

Т3: Через каждую из двух скрещивающихся прямых проходит ____________________, параллельная другой прямой, и притом только одна.

№3 В параллелепипеде (см. рис.) укажите параллельные прямые, на которых лежат его ребра.

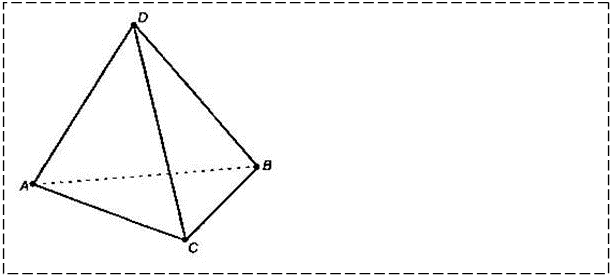
№4 В тетраэдре (см. рис.) укажите все пары скрещивающихся прямых, на которых лежат его ребра.

№5 Через точку А (см. рис.) в пространстве, не принадлежащую данной прямой a, проведите прямую, параллельную данной. Опишите построение. Сколько решений имеет задача?

№6 Исходя из данного рисунка, отметьте номера верных утверждений.

1. Прямые AD и CG скрещиваются.

2. Прямы AF и DC скрещиваются.

3. Прямы AO DF скрещиваются.

4. Прямы CF AB пересекаются.

5. Прямы DO AC пересекаются.

6. Прямая BF и плоскость ADC пересекаются.

7. Плоскость GOE и прямая AD пересекаются.

8. Прямые OF и AD скрещиваются.

№7 Решите задания на готовых чертежах

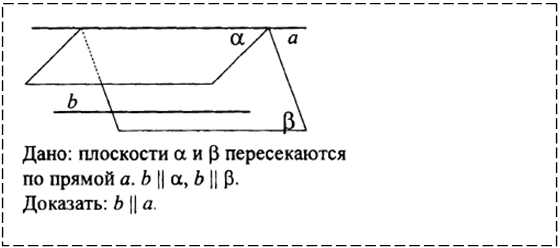
1.

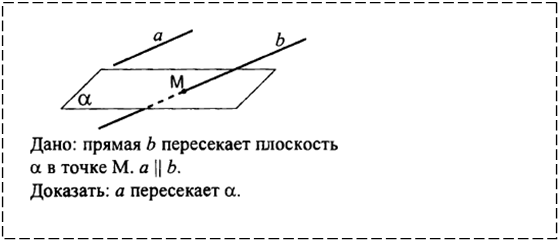
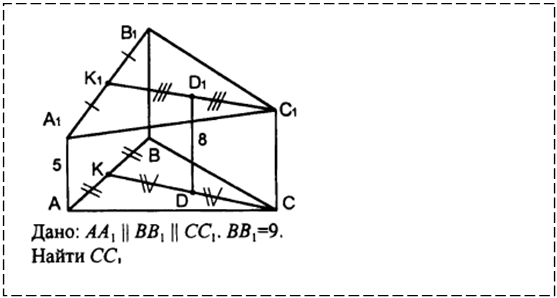
2.

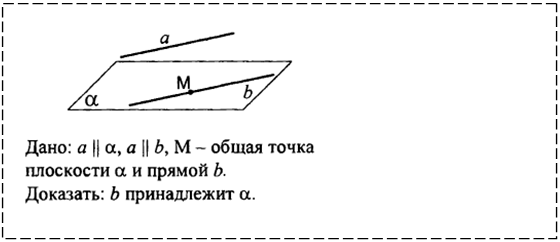
3.

4.

Параллельность прямой и плоскости

№1 Вставьте пропуски

Опр1: Прямая и плоскость называются параллельными, если они ________________________________.

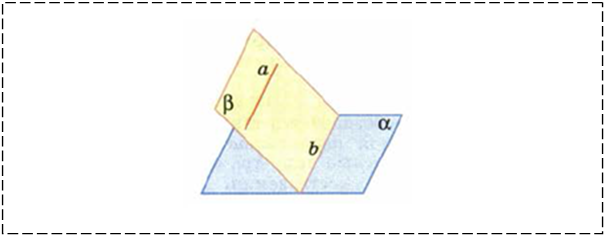
Т1: Если прямая, не лежащая в данной плоскости, __________________ какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

С1: Если плоскость проходит через данную прямую, параллельную другой плоскости, и ______________ эту плоскость, то линия _________________ плоскостей параллельна данной ________________.

С2: Если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая либо также параллельна данной плоскости, либо _____________________.

№3 Используя признак параллельности прямой и плоскости, укажите несколько пар параллельных прямой и плоскости в четырехугольной призме (см. рис.).

№4 Отметьте верные утверждения

1. Прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.

2. Существует единственная прямая, параллельная данной плоскости и проходящая через точку, не принадлежащую этой плоскости.

3. Существует бесконечное множество прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.

4. Через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.

5. Существует единственная плоскость, параллельная данной прямой и проходящая через точку, не принадлежащую этой прямой.

6. Существует бесконечное множество плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.

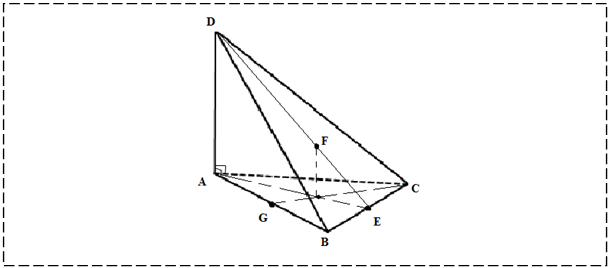
№5 На рисунке изображен треугольник АВС, не лежащий в плоскости α. Прямые АВ и ВС пересекают плоскость α соответсвенно в точках D и E. Постройте на чертеже: точку F пересечения прямой АС с плоскостью α; прямую k, лежащую в плоскости треугольника, проходящую через точку А и параллельную плоскости α.

№6 Выполните задания на готовых чертежах

1. 
2. 
3. 
4. 
5. 

№7 Решить задачу

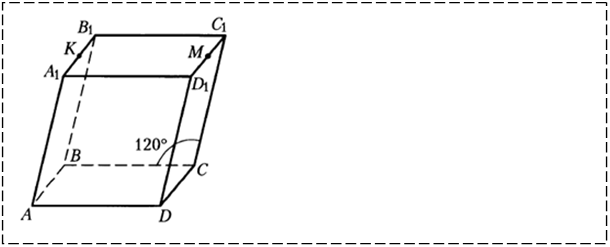
На рисунке ABCD- параллелограмм, ˪BCC₁=120° AA₁=BB₁=CC₁=DD₁ и AA₁||BB₁||CC₁||DD₁ .

1. Постройте линию пересечения OO₁ плоскостей, проходящих через прямую AA₁ и точку M и прямую DD₁ и точку K.

2. Каково взаимное расположение прямых OO₁ и AA₁?

3. Чему равен угол между прямыми OO₁ и AD?