 |
Главная |
Локальная гладкость приближенного решения МКСЭ
|
из
5.00
|
Если при аппроксимации решения в пространстве 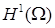 для ошибки решения, очевидно, справедлива эквивалентность
для ошибки решения, очевидно, справедлива эквивалентность 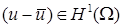
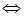
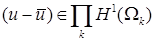
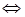
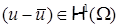 , то в пространствах более высокой гладкости
, то в пространствах более высокой гладкости 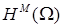 ,
, 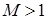 , и многоугольной границей разбиения
, и многоугольной границей разбиения 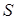 подобное несправедливо. Более того, показатель гладкости произвольной функции
подобное несправедливо. Более того, показатель гладкости произвольной функции 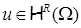 на
на 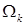 , имеющей гладкие следы на частях негладкой границы
, имеющей гладкие следы на частях негладкой границы 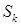 , ограничен сверху [13]. Это относится к регулярности решения задачи Дирихле в отдельном СЭ
, ограничен сверху [13]. Это относится к регулярности решения задачи Дирихле в отдельном СЭ 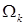 [32; 33; 24]. Ограничение по гладкости может оказаться достаточно жестким и связано с локальным поведением решения в суперэлементных углах. Показатель гладкости зависит как от гладкости правой части граничного условия на отдельных сторонах границы
[32; 33; 24]. Ограничение по гладкости может оказаться достаточно жестким и связано с локальным поведением решения в суперэлементных углах. Показатель гладкости зависит как от гладкости правой части граничного условия на отдельных сторонах границы 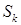 , их совместности в вершинах углов, так и от величины раствора углов, кривизны их сторон и вида исходного уравнения.
, их совместности в вершинах углов, так и от величины раствора углов, кривизны их сторон и вида исходного уравнения.
3.1. Свойства гладкости приближенного решения МКСЭ
Пусть Λ – один из углов СЭ с границей 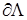 раствора α,
раствора α, 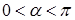 ; P – его вершина;
; P – его вершина; 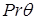 – полярная система координат, связанная с Λ. В данном пункте мы рассмотрим преимущественно отдельный угол Λ, полученные таким образом результаты обобщаются на всю расчетную область.
– полярная система координат, связанная с Λ. В данном пункте мы рассмотрим преимущественно отдельный угол Λ, полученные таким образом результаты обобщаются на всю расчетную область.
Помимо самого приближенного решения 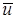 исследуем также его интерполянт
исследуем также его интерполянт 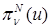 . Отметим, что все полученные здесь результаты для
. Отметим, что все полученные здесь результаты для 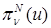 справедливы и для приближенного решения
справедливы и для приближенного решения 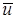 , а коэффициенты в его разложении, указанные через интерполянт
, а коэффициенты в его разложении, указанные через интерполянт 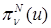 , должны быть заменены аналогичными, заданными через приближенное решение
, должны быть заменены аналогичными, заданными через приближенное решение 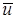 .
.
Интерполянт 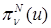 МКСЭ в области СЭ
МКСЭ в области СЭ 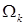 является решением задачи:
является решением задачи:
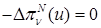 в
в 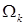 ,
,
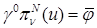 на
на 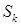 ,
,
где 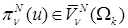 ,
, 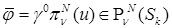 – граничный сплайн-интерполянт решения. Дальнейшие выкладки мы проводим в предположении, что следы совместны для всех углов Λ в СЭ
– граничный сплайн-интерполянт решения. Дальнейшие выкладки мы проводим в предположении, что следы совместны для всех углов Λ в СЭ 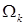 так, что
так, что
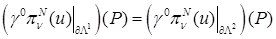 ,
,
и аналогично для приближенного решения:
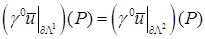 ,
,
где 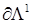 и
и 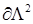 – отдельные стороны угла Λ, составляющие его границу
– отдельные стороны угла Λ, составляющие его границу 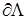 и пересекающиеся в точке P.
и пересекающиеся в точке P.
Утверждение 1 . Пусть граничные базисные функции МКСЭ в некоторой окрестности угла Λ СЭ 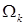 , на его границах
, на его границах 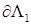 и
и 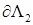 , – полиномы порядка не выше ν. Интерполянт приближенного решения
, – полиномы порядка не выше ν. Интерполянт приближенного решения 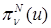 МКСЭ в этой окрестности представим в виде:
МКСЭ в этой окрестности представим в виде:
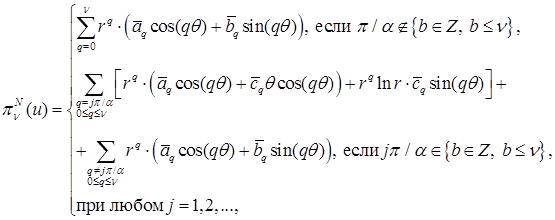
где
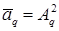 ,
, 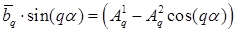 ,
, 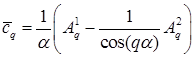 ,
,
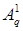 ,
, 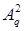 – коэффициенты решения (граничного полинома
– коэффициенты решения (граничного полинома 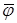 ) на границах
) на границах 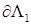 ,
, 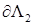 перед
перед 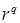 ,
, 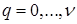 . Аналогичное утверждение справедливо и для приближенного решения
. Аналогичное утверждение справедливо и для приближенного решения 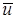 .
.
Доказательство. Будем искать решение задачи – в угле Λ СЭ как сумму решений 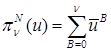 задач следующего вида:
задач следующего вида:
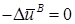 в
в 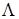 ,
,
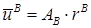 на
на 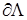 ,
,
где 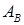 – константы,
– константы, 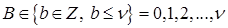 . При этом
. При этом 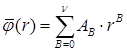 на
на 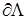 . Согласно [17, с. 47] асимптотика этой задачи в угле Λ такова:
. Согласно [17, с. 47] асимптотика этой задачи в угле Λ такова:
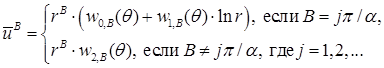
Здесь коэффициенты разложения по переменной r (функции 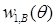 ,
, 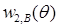 и
и 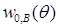 ) бесконечно дифференцируемы по θ (*).
) бесконечно дифференцируемы по θ (*).
Получим представление интерполянта приближенного решения:
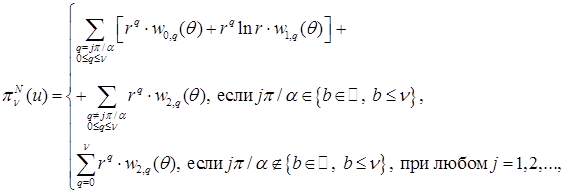
где 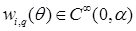
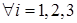 .
.
Уточним результат, рассмотрев константные коэффициенты разложений. Они представляют интерес для дальнейшего рассмотрения. Выбранные полиномиальные граничные значения бесконечно дифференцируемы в окрестности угла. Решение задачи согласно результату [17, с. 50] может быть найдено в виде:
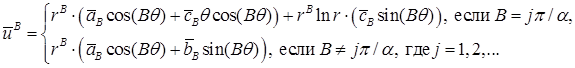
Находим коэффициенты 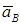 ,
, 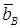 ,
, 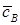 , подставляя в задачу . Тогда
, подставляя в задачу . Тогда
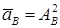 ,
, 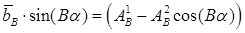 ,
, 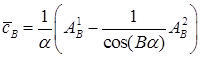 ,
,
где 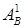 ,
, 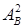 – коэффициенты граничных значений
– коэффициенты граничных значений 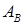 для различных сторон угла
для различных сторон угла 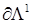 и
и 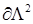 соответственно. Граница
соответственно. Граница 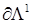 соответствует значениям угла
соответствует значениям угла 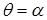 , и
, и 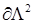 – значению
– значению 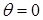 .
.
Отметим, что в первой сумме выражения 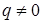 . Суммирование по всем B дает разложение приближенного решения
. Суммирование по всем B дает разложение приближенного решения 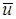 в области Λ (где символ B заменен на q):
в области Λ (где символ B заменен на q):
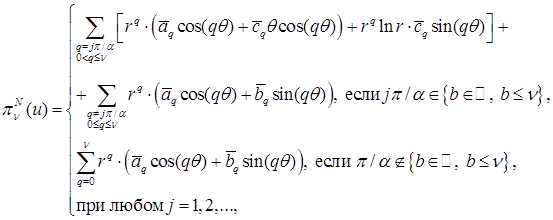
с коэффициентами , 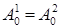 ,
, 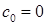 . Выпишем слагаемое при
. Выпишем слагаемое при 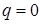 :
:
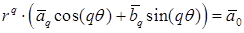
в обоих случаях принадлежности 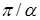 . #
. #
Замечание. Из проведенного рассмотрения следует также: 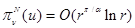 ,
, 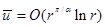 при
при 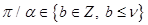 ,
, 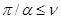 ; в противном случае решение
; в противном случае решение 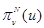 и
и 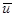 ограничено.
ограничено.
Пример. Для угла квадратного СЭ значение 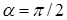 . Приближенное решение МКСЭ
. Приближенное решение МКСЭ 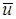 , а также его интерполянт в некоторой окрестности углов СЭ представимы в виде следующей конечной суммы:
, а также его интерполянт в некоторой окрестности углов СЭ представимы в виде следующей конечной суммы:
при линейной интерполяции граничного решения
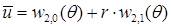 ;
;
при любой полиномиальной интерполяции порядка выше единицы:
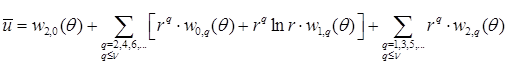 . #
. #
Выражение определяет гладкость интерполянта приближенного решения 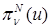 МКСЭ в соболевских пространствах. Если
МКСЭ в соболевских пространствах. Если 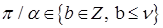 и
и 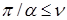 , то
, то 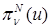 нерегулярна по отношению к граничному условию так, что
нерегулярна по отношению к граничному условию так, что 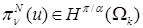 для произвольных
для произвольных 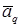 ,
, 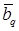 ,
,  . В противном случае решение в угле Λ обладает бесконечной гладкостью, поэтому приближенное решение в СЭ
. В противном случае решение в угле Λ обладает бесконечной гладкостью, поэтому приближенное решение в СЭ 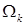 имеет максимальную гладкость по отношению к граничному условию на
имеет максимальную гладкость по отношению к граничному условию на 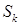 . То же относится к приближенному решению
. То же относится к приближенному решению 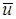 МКСЭ.
МКСЭ.
Рассмотрим пространство 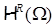 . Согласно в его определение включено условие . Мы вводим ещё одно важное предположение о совместности следов в узлах
. Согласно в его определение включено условие . Мы вводим ещё одно важное предположение о совместности следов в узлах 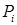 СЭ, а именно:
СЭ, а именно: 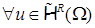 считаем выполненным условие
считаем выполненным условие
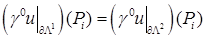
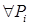 .
.
Считаем также, что все углы СЭ направлены во внешность их области: 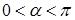 . Пространство
. Пространство 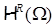 , дополненное условием совместности следов , и условием
, дополненное условием совместности следов , и условием 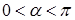 на раствор углов, обозначим
на раствор углов, обозначим 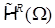 .
.
Утверждение 2 . Приближенное решение МКСЭ из пространства 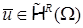 принадлежит соболевскому пространству
принадлежит соболевскому пространству 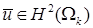 в пределах каждого СЭ
в пределах каждого СЭ 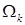 . То же верно для интерполянта
. То же верно для интерполянта 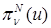 .
.
Доказательство. Предыдущие выкладки показывают, что 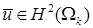 в области СЭ
в области СЭ 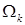 , если
, если 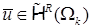 . Нерегулярный случай
. Нерегулярный случай 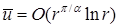 при минимальном значении
при минимальном значении 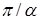 из множества
из множества 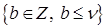 дает
дает 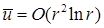 . Значит, выполнено
. Значит, выполнено 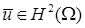 . Аналогично для
. Аналогично для 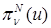 . Заметим, что для дальнейших выкладок это не принципиально, но упрощает некоторые записи. #
. Заметим, что для дальнейших выкладок это не принципиально, но упрощает некоторые записи. #
3.2. Асимптотическое разложение функции класса HR(Λ)
Приведем некоторые известные сведения об асимптотическом разложении некоторой функции в многоугольном СЭ. Совместно с пунктом 0 эта информация может быть употреблена для получения ряда оценок. Кроме того, она дает представление и о других возможных вариантах задания граничных базисных функций, не указанных ранее и характеризуемых любой гладкостью по шкале Соболева. Как мы уже отмечали, показатель гладкости такой функции в СЭ всегда ограничен сверху. Это связано с гладкостью 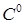 его границы. Получим асимптотическое разложение в окрестностях угловых точек.
его границы. Получим асимптотическое разложение в окрестностях угловых точек.
Произвольное решение уравнения Лапласа с граничными данными 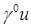 в угле Λ СЭ
в угле Λ СЭ 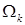 (в некоторой окрестности угловой точки P) разложимо в сумму гладкой и сингулярной частей [24; 25; 35]:
(в некоторой окрестности угловой точки P) разложимо в сумму гладкой и сингулярной частей [24; 25; 35]:
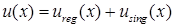 ,
, 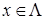 ,
,
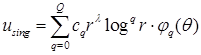 ,
,
где 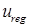 обладает максимальной гладкостью, порожденной гладкостью функции
обладает максимальной гладкостью, порожденной гладкостью функции 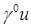 граничного условия, а наличие
граничного условия, а наличие 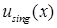 обусловлено видом области Λ. Здесь
обусловлено видом области Λ. Здесь 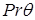 – локальная система координат в угле Λ; набор параметров λ определен некоторыми характеристическими числами, связанными с уравнением, и может быть дополнен конечным числом положительных действительных параметров
– локальная система координат в угле Λ; набор параметров λ определен некоторыми характеристическими числами, связанными с уравнением, и может быть дополнен конечным числом положительных действительных параметров 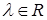 ,
, 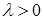 ; причем и в том, и в другом случае диапазон λ ограничен сверху гладкостью граничных данных; Q – конечное число;
; причем и в том, и в другом случае диапазон λ ограничен сверху гладкостью граничных данных; Q – конечное число; 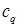 – константы. Рассматриваемое нами эллиптическое уравнение не содержит членов порядка меньше максимального. Кроме того, границы
– константы. Рассматриваемое нами эллиптическое уравнение не содержит членов порядка меньше максимального. Кроме того, границы 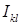 СЭ в некоторой окрестности каждого из углов Λ считаем прямыми линиями.
СЭ в некоторой окрестности каждого из углов Λ считаем прямыми линиями.
Классическим способом определения регулярности решения линейного эллиптического уравнения с постоянными коэффициентами является метод В.А. Кондратьева(*), использующий преобразование Меллина [21] исходного уравнения в угле Λ в задачу на отрезке 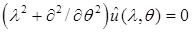 ,
, 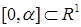 ,
, 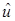 – изображение. Выписанное уравнение на собственные значения
– изображение. Выписанное уравнение на собственные значения 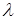 можно получить и определенной заменой переменных, преобразовывающей задачу в угле в задачу на некоторой простой области, например, полосе [17], полупространстве [33] в случае уравнения Лапласа. Несложно определить его решение как решение задачи Штурма-Лиувилля. Оно имеет вид:
можно получить и определенной заменой переменных, преобразовывающей задачу в угле в задачу на некоторой простой области, например, полосе [17], полупространстве [33] в случае уравнения Лапласа. Несложно определить его решение как решение задачи Штурма-Лиувилля. Оно имеет вид: 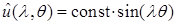 ,
, 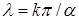 ,
, 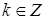 . Обратное преобразование Меллина даст разложение решения:
. Обратное преобразование Меллина даст разложение решения: 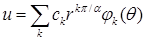 , где
, где 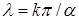 принадлежит конечному промежутку,
принадлежит конечному промежутку, 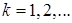
В случае уравнения Лапласа коэффициенты λ разложения включают в себя конечный ряд из полученных характеристических чисел 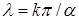 для
для 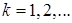 [25; 32].
[25; 32].
Наличие неоднородных граничных условий на 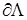 приводит к возникновению дополнительных слагаемых в таком разложении, гладкость которых измеряется в пространствах Соболева с весом
приводит к возникновению дополнительных слагаемых в таком разложении, гладкость которых измеряется в пространствах Соболева с весом 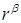 [35]. Для определения их полной асимптотики и регулярности в рамках шкалы “обыкновенных” пространств Соболева требуется дополнительное исследование. Например, полиномиальная правая часть в угле раствора
[35]. Для определения их полной асимптотики и регулярности в рамках шкалы “обыкновенных” пространств Соболева требуется дополнительное исследование. Например, полиномиальная правая часть в угле раствора 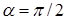 (см. пункт 0) приводит к разложению с порядком
(см. пункт 0) приводит к разложению с порядком 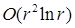 . Величина
. Величина 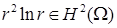 регулярна при рассмотрении пространства с показателем гладкости
регулярна при рассмотрении пространства с показателем гладкости 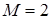 , она регулярна также и для некоторых пространств Соболева с весом. При работе в шкале соболевских пространств
, она регулярна также и для некоторых пространств Соболева с весом. При работе в шкале соболевских пространств 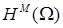 ,
, 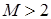 , её уже необходимо учитывать как нерегулярную часть. Отметим, что шкала весовых пространств “с однородной нормой”, возникающих при использовании метода Кондратьева, не имеет пересечений со шкалой пространств Соболева
, её уже необходимо учитывать как нерегулярную часть. Отметим, что шкала весовых пространств “с однородной нормой”, возникающих при использовании метода Кондратьева, не имеет пересечений со шкалой пространств Соболева 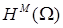 [32]. Мы ее не используем.
[32]. Мы ее не используем.
Нас интересует множество функций, удовлетворяющих уравнению Лапласа в областях 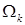 , условиям и со следами класса
, условиям и со следами класса 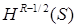 ,
, 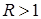 . Ранее оно было обозначено через
. Ранее оно было обозначено через 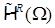 . Вообще говоря, пространство
. Вообще говоря, пространство 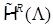 в угле Λ содержит в себе набор весовых пространств “с неоднородной нормой”
в угле Λ содержит в себе набор весовых пространств “с неоднородной нормой” 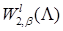 , см. [32], характеризующийся индексами
, см. [32], характеризующийся индексами 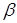 ,
, 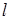
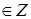 определенного диапазона. Уточнение асимптотики выражения – со следами из
определенного диапазона. Уточнение асимптотики выражения – со следами из 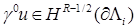 ,
, 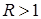 , может быть выписано согласно [32, p.p. 284, 300]. А именно, в угле Λ справедливо представление:
, может быть выписано согласно [32, p.p. 284, 300]. А именно, в угле Λ справедливо представление:
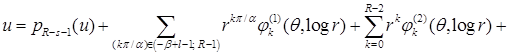
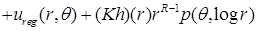 ,
,
где 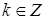 ,
, 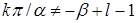 ;
; 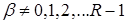 ;
; 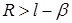 ;
; 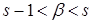 для некоторого
для некоторого 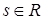 . Слагаемое
. Слагаемое 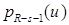 является полиномом от функции u порядка не выше
является полиномом от функции u порядка не выше 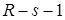 . Функции
. Функции 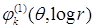 ,
, 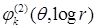 ,
, 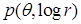 – полиномы от переменной
– полиномы от переменной 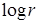 с коэффициентами (зависящими от
с коэффициентами (зависящими от 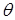 ) класса
) класса 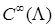 . Функция
. Функция 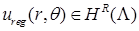 обладает максимальной гладкостью по отношению к заданному граничному условию
обладает максимальной гладкостью по отношению к заданному граничному условию 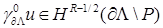 . Функция
. Функция 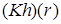 действует в пространство
действует в пространство 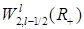
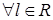 ,
, 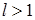 . Из общих теорем вложения для данных весовых пространств (напр., [26]) следует, что
. Из общих теорем вложения для данных весовых пространств (напр., [26]) следует, что 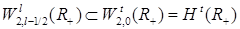 для
для 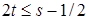 . При этом для функции u при
. При этом для функции u при 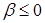 справедливо условие
справедливо условие 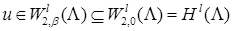 .
.
Такое разложение достаточно громоздко, но содержит все необходимые нам факты, связанные с асимптотикой 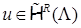 в угле СЭ. Подчеркнем, что вид разложения является общим, его коэффициенты могут зависеть от раствора угла [33], величины R, граничных условий [37] и т.п.
в угле СЭ. Подчеркнем, что вид разложения является общим, его коэффициенты могут зависеть от раствора угла [33], величины R, граничных условий [37] и т.п.
Заметим, что для 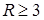 , асимптотика содержит слагаемое
, асимптотика содержит слагаемое 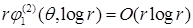 , его гладкость не выше
, его гладкость не выше 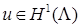 . Для
. Для 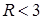 в общем случае для решения справедливо соотношение
в общем случае для решения справедливо соотношение 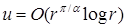 . При этом
. При этом 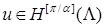 , где
, где 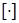 – обозначение целой части числа. Если
– обозначение целой части числа. Если 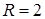 , то первая сумма содержит слагаемые только в случае угла
, то первая сумма содержит слагаемые только в случае угла 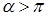 .
.
Отсюда для пространства 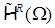 следует вложение
следует вложение
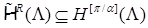 .
.
Напомним, что из общего определения выполнено вложение вида
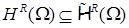 ,
, 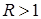 .
.
Отметим, что достаточно хорошо известны результаты и оценки, связанные с сильным решением задачи Дирихле 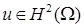 в многоугольной области
в многоугольной области 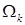 (см. [22; 23]). При этом достаточно легко заметить, что все соотношения в данных работах полностью согласуются с выписанным разложением . Мы не используем данные результаты, поскольку нас интересует весь диапазон возможной гладкости. Используем асимптотику либо её более общий вид . Последующие рассуждения относятся к уточнению таких оценок, что не представляется возможным, оставаясь лишь в рамках шкалы
(см. [22; 23]). При этом достаточно легко заметить, что все соотношения в данных работах полностью согласуются с выписанным разложением . Мы не используем данные результаты, поскольку нас интересует весь диапазон возможной гладкости. Используем асимптотику либо её более общий вид . Последующие рассуждения относятся к уточнению таких оценок, что не представляется возможным, оставаясь лишь в рамках шкалы 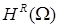 .
.
Введем ещё одно определение. Оператор следа m-го порядка 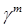 в пространстве
в пространстве 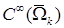 задан соотношением
задан соотношением
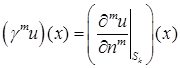 ,
, 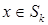 ,
,
где n – внешняя единичная нормаль к границе 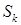 ,
, 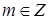 . Оператор
. Оператор 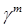 действует из
действует из 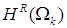 в
в 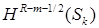 для
для 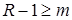 , и допускает “обычное” расширение в слабом смысле, например,
, и допускает “обычное” расширение в слабом смысле, например, 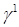 :
: 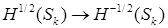 для
для 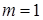 .
.
4. Оценки решения по шкале HM(Ω)
Пусть задача – обладает гладким решением 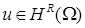 ,
, 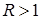 . Рассмотрим вопрос об аппроксимации первых производных
. Рассмотрим вопрос об аппроксимации первых производных 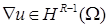 , как и ранее, в норме пространства
, как и ранее, в норме пространства 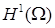 . Из того факта, что
. Из того факта, что
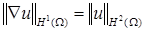 ,
,
следует, что нам нужны оценки погрешностей решения u в норме пространства 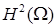 . Обобщая на произвольный порядок производных
. Обобщая на произвольный порядок производных 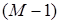 ,
, 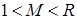 ,
, 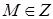 , можно исследовать поведение погрешностей решения u в нормах пространств
, можно исследовать поведение погрешностей решения u в нормах пространств 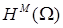 и, следовательно, определяя свойства МКСЭ о приближении производных порядка
и, следовательно, определяя свойства МКСЭ о приближении производных порядка 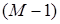 в норме пространства Соболева
в норме пространства Соболева  .
.
Рассмотрим пример M = 2. Из гармоничности градиентов искомого и приближенного решений имеем
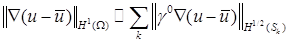 ,
,
где, вообще говоря, 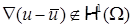 , так как условие совместности для градиентов не выполнено. Пункт 0 показывает, что
, так как условие совместности для градиентов не выполнено. Пункт 0 показывает, что 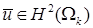 в области СЭ
в области СЭ 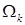 , если
, если 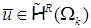 , поэтому запись ошибки решения в норме
, поэтому запись ошибки решения в норме 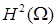 корректна.
корректна.
Запишем с использованием стандартных преобразований:
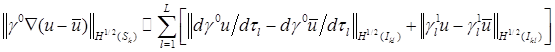 ,
,
где 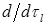 – производная по направлению касательного вектора
– производная по направлению касательного вектора 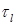 на отрезке
на отрезке 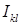 ;
; 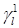 – след первого порядка
– след первого порядка 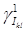 на
на 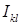 , см. .
, см. .
Если бы выражение для ошибки 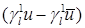 допускало принадлежность классу
допускало принадлежность классу 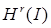 ,
, 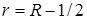 ,
, 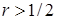 , на отдельном отрезке
, на отдельном отрезке 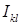 , то стала бы возможной запись неравенства
, то стала бы возможной запись неравенства 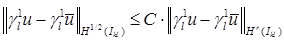 как следствие непрерывного вложения соответствующих пространств. Тогда слагаемые под знаком нормы в правой части выражения оценивались бы согласно “стандартным” выкладкам [10–12]. Заметим, что здесь нас интересуют не только априорные оценки погрешностей производных, но и сама сходимость производных приближенного решения МКСЭ к точному решению.
как следствие непрерывного вложения соответствующих пространств. Тогда слагаемые под знаком нормы в правой части выражения оценивались бы согласно “стандартным” выкладкам [10–12]. Заметим, что здесь нас интересуют не только априорные оценки погрешностей производных, но и сама сходимость производных приближенного решения МКСЭ к точному решению.
Ясно, что 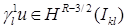 . Для следа первого порядка (нормальной производной) приближенного решения
. Для следа первого порядка (нормальной производной) приближенного решения 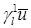 на отрезке
на отрезке 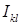 нет точного аналитического выражения, оно известно лишь для следа
нет точного аналитического выражения, оно известно лишь для следа 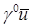 . Можно определить регулярность
. Можно определить регулярность 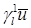 лишь в окрестности узлов
лишь в окрестности узлов 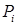 , благодаря пункту 0.
, благодаря пункту 0.
Рассмотрим далее угол Λ, поэтому через 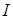 будем обозначать произвольную его сторону
будем обозначать произвольную его сторону 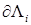 ; как и ранее, P – вершина угла Λ.
; как и ранее, P – вершина угла Λ.
Несложно показать, что на границе угла 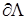 справедливо равенство:
справедливо равенство:
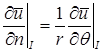 .
.
Тогда из разложения для интересующего диапазона 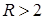 получим следующий результат:
получим следующий результат:
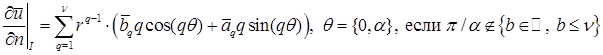 ;
;
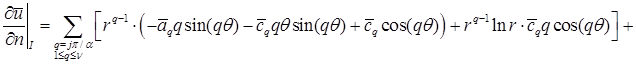
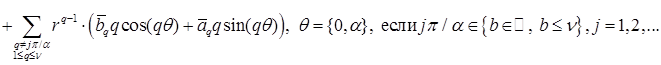 Отметим, что первым слагаемым, характерным для каждого из разложений и имеющим минимальный показатель
Отметим, что первым слагаемым, характерным для каждого из разложений и имеющим минимальный показатель 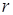 (либо
(либо 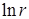 ) является величина
) является величина 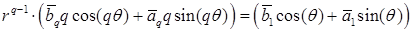 при
при 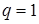 , зависящая от переменной
, зависящая от переменной 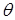 . Здесь также
. Здесь также 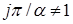 , поскольку
, поскольку 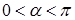 .
.
Перепишем полученные выражения, подставляя 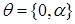 во вторую сумму(*):
во вторую сумму(*):
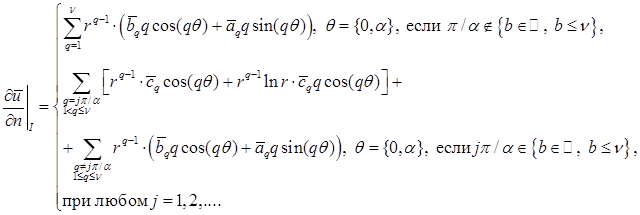 Отсюда ясно, что в окрестности вершины P произвольного угла СЭ Λ раствора α справедливы соотношения:
Отсюда ясно, что в окрестности вершины P произвольного угла СЭ Λ раствора α справедливы соотношения: 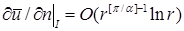 и
и 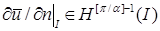 для
для 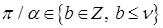 или производная
или производная 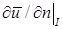 регулярна, если
регулярна, если 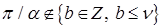 .
.
Более того, свойства гладкости 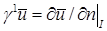 можно определить, воспользовавшись следующими результатами.
можно определить, воспользовавшись следующими результатами.
Утверждение 3 [26]. Элемент 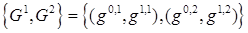 из пространства
из пространства 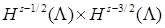 является образом некоторой функции
является образом некоторой функции 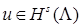 в угле
в угле 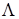 раствора α с вершиной P в результате действия согласно оператора
раствора α с вершиной P в результате действия согласно оператора 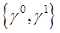 , тогда и только тогда, когда выполнены соотношения
, тогда и только тогда, когда выполнены соотношения
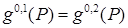 ,
,
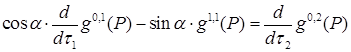 ,
,
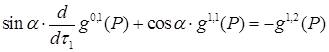 ,
,
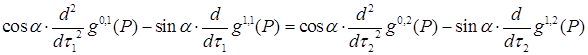
и для 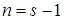 ,
, 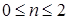 , выполнено некоторое интегральное условие, где
, выполнено некоторое интегральное условие, где 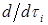 – существующие конечные производные по отношению к касательным векторам
– существующие конечные производные по отношению к касательным векторам 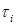 для границы
для границы 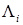 ,
, 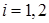 .
.
В том случае, когда 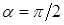 , условия – принимают вид:
, условия – принимают вид:
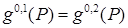 ,
,
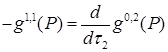 ,
,
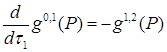 ,
,
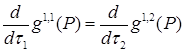
и для 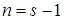 ,
, 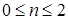 ,
,
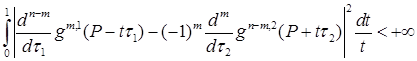 , при
, при 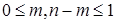 .
.
Отметим, что число условий совместности ограничено, несмотря на увеличение показателя s. Это связано с тем, что мы исследуем лишь величины 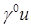 и
и 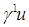 ; это число таким образом связано непосредственно с порядком рассматриваемой нормы M.
; это число таким образом связано непосредственно с порядком рассматриваемой нормы M.
Вариант 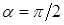 выписан для примера вследствие простоты записи. Не составляет труда перенести результаты на общий случай. Для квадратного СЭ
выписан для примера вследствие простоты записи. Не составляет труда перенести результаты на общий случай. Для квадратного СЭ 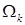 с узлами
с узлами 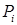 и сторонами
и сторонами 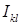 ,
, 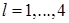 ,
, 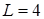 , справедливо утверждение.
, справедливо утверждение.
Утверждение 4 [26]. Пусть 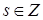 и
и 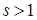 . Элемент
. Элемент 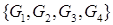 ,
, 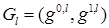 ,
, 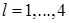 , из пространства
, из пространства 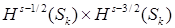 есть образ при отображении
есть образ при отображении 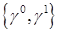 некоторой функции из пространства Соболева
некоторой функции из пространства Соболева 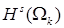 тогда и только тогда, когда для всех
тогда и только тогда, когда для всех 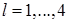 и для всех
и для всех 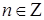 ,
, 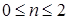 ,
, 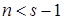 , выполнено
, выполнено
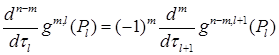 , где
, где 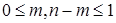 ,
,
для 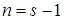 ,
, 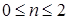 , выполнено
, выполнено
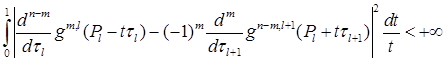 ,
,
и принято обозначение 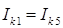 ,
, 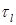 – касательные вектора для границы
– касательные вектора для границы 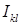 .
.
Замечание Пространство 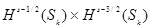 , дополненное набором таких условий, не является замкнутым в
, дополненное набором таких условий, не является замкнутым в 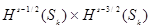 в стандартной норме. Оператор
в стандартной норме. Оператор 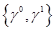 непрерывно действует из
непрерывно действует из 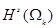 в такое модифицированное пространство и допускает непрерывный обратный при s > 2 в том случае, когда оно снабжено нормой с добавлением слагаемого, совпадающего с левой частью или , см. также [26].#
в такое модифицированное пространство и допускает непрерывный обратный при s > 2 в том случае, когда оно снабжено нормой с добавлением слагаемого, совпадающего с левой частью или , см. также [26].#
Таким образом, для исследования свойств нормальной производной


