 |
Главная |
Обобщенный алгоритм решения задачи синтеза структур нестационарных ARC-схем
|
из
5.00
|
Полученный результат показывает, что задача синтеза структур нестационарных устройств сводится к аналогичной стационарной задаче в точке «наихудшего случая», когда совокупность управляющих параметров из множества допустимых параметрических воздействий приводит к максимальному отклонению частотных характеристик от желаемых. Таким образом, согласно предложенной в настоящей работе методологии синтеза структур рассматриваемую задачу можно разделить на три относительно самостоятельных этапа.
Первый этап заключается в синтезе исходной принципиальной схемы, получении набора локальных передаточных функций, определяющих функции активной составляющей чувствительности, и принятии решения о направлении проектных процедур. Настоящий этап состоит из ряда составляющих. Прежде всего, по модели нестационарного устройства синтезируется стартовая конфигурация принципиальной схемы. По стартовой конфигурации путем коммутации базисных структур строится принципиальная схема аналоговой части проектируемого устройства, воспроизводящая заданный набор «замороженных» передаточных функций. Выбор числа разрядов умножающих ЦАП, входящих в состав управляемых усилителей и интеграторов, может осуществляться по следующей оценочной формуле:
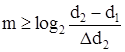 ,
,
где d1 и d2 – верхняя и нижняя границы диапазона измеряемой величины; D – шаг квантования по уровню, который выбирается из соображений точности реализации требуемых коэффициентов.
Для определения набора локальных передаточных функций Fsi(p), Fkj(p), Hi(p), Hj(p), Fii(p), Fjj(p) по синтезированной схеме достаточно вычислить обратную матрицу. Получение последней в символьном виде позволяет не только повысить наглядность представляемой информации, но и обеспечивает на последнем этапе синтеза согласованных с Fii(p), Fjj(p), Hi(p), Hj(p) законов изменения дополнительных компенсирующих цепей обратных связей. На этом же этапе становится возможным вычисление коэффициентов , определяющих верхний уровень динамического диапазона во всех стационарных точках x. Этап завершается определением функций чувствительности к площади усиления всех активных элементов.
На втором этапе синтеза, с целью выбора предпочтительного варианта реализации компенсирующих контуров обратных связей, необходимо определить доминирующие активные элементы, параметры которых наибольшим образом оказывают влияние на достижимый частотный и динамический диапазон схемы. Для ранжирования степеней влияния каждого ОУ наиболее целесообразно, с точки зрения рассматриваемой концепции синтеза, произвести исследование наборов модулей функций чувствительности с целью определения их максимума. Для этого прежде всего необходимо определить область изменения параметров схемы, соответствующую «наихудшему случаю», когда отклонение реализуемых функций амплитудно-частотных характеристик (АЧХ) и фазочастотных характеристик (ФЧХ) от идеальных в полосе рабочих частот схемы окажется максимальным:
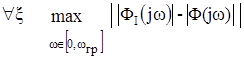 , (8)
, (8)
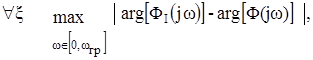 (9)
(9)
где 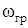 – максимальная граничная частота работы схемы.
– максимальная граничная частота работы схемы.
Значение оценки верхней границы частотного диапазона схемы для 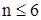 можно определить по формуле
можно определить по формуле
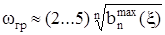 , (10)
, (10)
где 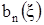 – свободный член полинома знаменателя идеализированной замороженной передаточной функции W0.
– свободный член полинома знаменателя идеализированной замороженной передаточной функции W0.
Отметим, что важно не только определить значение экстремума функций (8) и (9), но и найти координаты указанных глобальных экстремумов. На эти экстремальные задачи накладывается система ограничений в виде неравенств, следующая из максимально и минимально возможного коэффициента передачи ЦАП, масштабных усилителей, значения постоянной времени интеграторов и рабочего диапазона частот нестационарной схемы
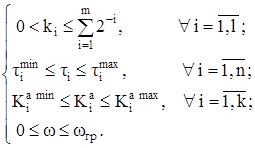 (11)
(11)
В частном случае из (11) могут быть исключены ограничения, соответствующие неизменяемым параметрам коэффициентов передачи масштабных усилителей или постоянным времени интеграторов.
Таким образом, в результате решения экстремальных задач (8) и (9) с ограничениями (11) становится возможным определение следующего вектора оптимальных координат:
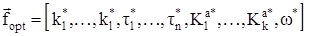 , (12)
, (12)
соответствующего наихудшему случаю.
С учетом результатов (12) для ранжирования ОУ по степени их влияния находится решение следующей экстремальной задачи с соответствующей системой ограничений:
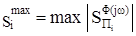 , (13)
, (13)
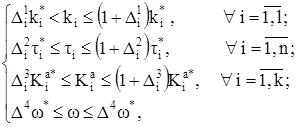 (14)
(14)
где 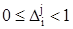 – относительный доверительный интервал решения экстремальной задачи.
– относительный доверительный интервал решения экстремальной задачи.
Указанный доверительный интервал необходим вследствие того, что максимумы модулей функций чувствительности в общем случае не совпадают с определенной оптимальной точкой (12), а лишь находятся в ее окрестности [9].
Выражение (14) является интегральной оценкой, позволяющей произвести качественный анализ влияния площади усиления i-го ОУ на частотные свойства передаточных функций. Успешное решение экстремальных задач (8), (9) и (13) во многом зависит от специфики работы нестационарного устройства, диапазона изменения управляющих параметров и требований, предъявляемых к точности реализации.
Для визуальной оценки степени влияния параметров каждого ОУ по результатам проведенных исследований (13) строится набор диаграмм по каждому из выходов, из которых можно определить доминирующий активный элемент
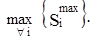 (15)
(15)
Следует отметить, что функциональные зависимости коэффициента передачи ЦАП 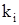 , масштабного усилителя
, масштабного усилителя 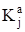 и постоянной времени интегратора
и постоянной времени интегратора 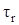 определяются дискретным моментом (интервалом) времени
определяются дискретным моментом (интервалом) времени 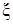 , поэтому функции (8), (9), (13) и соответствующие им системы ограничений (11) и (14), а также вектор оптимальных координат (12) яв-ляются значениями только двух параметров
, поэтому функции (8), (9), (13) и соответствующие им системы ограничений (11) и (14), а также вектор оптимальных координат (12) яв-ляются значениями только двух параметров 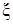 и
и 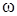 . Однако для примене-ния оптимизационных методов решения этих экстремальных задач, не свя-занных в общем случае с прямым перебором возможных комбинаций зна-чений параметров оптимизируемых функций, целесообразной оказывается приведенная выше форма представления указанных выражений.
. Однако для примене-ния оптимизационных методов решения этих экстремальных задач, не свя-занных в общем случае с прямым перебором возможных комбинаций зна-чений параметров оптимизируемых функций, целесообразной оказывается приведенная выше форма представления указанных выражений.
Задача третьего этапа синтеза связана с введением в схему дополни-тельных компенсирующих контуров обратной связи. В качестве нулевого приближения при проверке результатов синтезированных схемных решений целесообразно взять допустимое значение отклонения АЧХ реализуемой реальной схемы с замороженными коэффициентами от идеализированной. Допустимый коридор отклонений АЧХ определяется допустимыми значениями отклонений коэффициентов полиномов числителя и знаменателя замороженной пере-даточной функции (в точке (12)) от идеальных.
Чувствительность модуля передаточной функции Ф к изменению 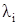 параметра можно представить следующим образом:
параметра можно представить следующим образом:
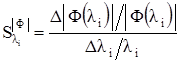 .
.
Представим замороженную передаточную функцию идеализированного устройства в следующем виде:
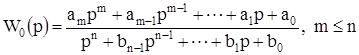 . (16)
. (16)
Тогда допустимое значение отклонения АЧХ можно определить по формуле
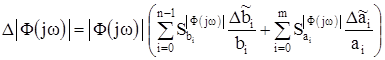 , (17)
, (17)
где 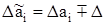 ,
, 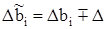 ;
; 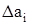 и
и 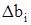 – допустимые отклонения значений коэффициентов полинома числителя и знаменателя передаточной функции (16);
– допустимые отклонения значений коэффициентов полинома числителя и знаменателя передаточной функции (16); 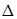 – приведенная максимальная статическая погрешность умножающих ЦАП.
– приведенная максимальная статическая погрешность умножающих ЦАП.
Значения 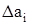 и
и 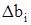 определяются допустимыми интервалами изменения элементов вектора отклонений, следующего из решения системной задачи.
определяются допустимыми интервалами изменения элементов вектора отклонений, следующего из решения системной задачи.
Процедура синтеза низкочувствительной схемы заключается во введении в последнюю дополнительных компенсирующих контуров обратной связи и носит итерационный характер [8]:
- по оценкам, полученным на втором этапе синтеза, выбирается доминирующий активный элемент;
- для выбора предпочтительного варианта реализации компенсирующих контуров обратных связей производится поиск необходимого набора локальных передач, поиск производится по строке матрицы 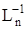 ; если необходимых передач нет, то последние ищутся по всей матрице, исключая элементы главной диагонали;
; если необходимых передач нет, то последние ищутся по всей матрице, исключая элементы главной диагонали;
- для уменьшения влияния частотных свойств доминирующего ОУ на достижимый схемой частотный и динамический диапазоны в схему вводятся дополнительные компенсирующие контуры обратной связи и осуществляется ее параметрическая оптимизация;
- с целью проверки качества принятого в предыдущем пункте решения производится численное моделирование синтезируемой схемы в частотной области, например с помощью одного из современных пакетов программ;
- выход из алгоритма производится либо по достижении требуемых качеств проектируемого устройства (если они не удовлетворены, выбирается следующий по установленному ранжиру активный элемент), либо при исчерпывании всех степеней свободы схемы, количество которых определяется числом заземленных входов ОУ, при этом необходимо учитывать, что для обеспечения правильного режима работы схемы по постоянному току хотя бы один вход ОУ должен быть заземлен;
- с целью проверки качества синтезированных схемных решений производится численное моделирование синтезируемой схемы во временной области.
При получении неудовлетворительных результатов (невозможности достижения заданных требований к качеству проектируемого устройства) в исходной схеме, полученной на первом этапе синтеза, с целью перераспределения значений функций чувствительности необходимо выполнить иной выбор параметров базисных структур, после чего повторить приведенный выше алгоритм синтеза компенсирующих контуров обратных связей. Отмеченная ситуация, например, может возникнуть при синтезе компенсирующих контуров обратных связей, когда для достижения требуемого (достаточного) уровня компенсации влияния инерционных свойств i-го активного элемента на параметры схемы в дополнительном контуре обратной связи необходимо обеспечить большое усиление. Указанного можно достичь несколькими способами. В первом случае в схему вводится дополнительный усилитель, во втором в схеме выполняется иной выбор параметров базисных структур, который обеспечивает получение требуемых значений усиления в компенсирующих контурах схемы путем перераспределения усиления между ее функциональными узлами. В отличие от первого способа, второй не требует дополнительных аппаратных затрат.
Задача третьего этапа синтеза в части синтеза схемных решений не может быть полностью формализована – выбор предпочтительного варианта реализации компенсирующих контуров остается за проектировщиком.
Рассматриваемая задача может быть алгоритмизирована в виде некоторой экспертной системы, исходными данными для которой служат полный набор передаточных функций в символьном виде, полученных на первом этапе, и наборы оценок из второго этапа синтеза. Таким образом, в результате решения задачи последнего этапа проектирования возможно получить схемные решения, позволяющие создать схему с собственной компенсацией влияния частотных свойств активных элементов на ее параметры.
|
из
5.00
|
Обсуждение в статье: Обобщенный алгоритм решения задачи синтеза структур нестационарных ARC-схем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

