Составление уравнения движения твердого тела с помощью теоремы об изменении кинетического момента

Механической системой называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения остальных точек. Получаемые для системы материальных точек теоремы и соотношения можно распространить и на системы, состоящие из одного или нескольких взаимосвязанных твердых тел. Ограничения, накладываемые на движение точек и тел механической системы, называются связями. Исходя из принципа освобождаемости от связей, движение каждой точки системы можно рассматривать как движение свободной точки, если заменить действие связей реакциями этих связей. Тогда для каждой точки, согласно основному уравнению динамики материальной точки, имеем:

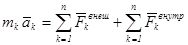 (3.1.1)

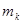 и 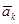 – масса и ускорение некоторой точки механической системы;  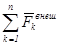и 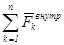 – внешние и внутренние силы (уже включают в себя реакции связей).

Уравнение (3.1.1) – это основное уравнение динамики, следствием его являются теоремы о движении центра масс механической системы и об изменении количества движения, теоремы об изменении кинетического момента и кинетической энергии. Теорема об изменении кинетического момента применяется для решения задач, в которых рассматривается движение механической системы, состоящей из центрального тела, вращающегося вокруг неподвижной оси, и одного или нескольких тел, движение которых связано с центральным. Связь может осуществляться при помощи нитей, тела могут перемещаться по поверхности центрального тела или в его каналах за счёт внутренних сил. С помощью данной теоремы можно определить зависимость закона вращения центрального тела от положения или движения остальных тел.

Теорема об изменении кинетического момента формулируется следующим образом: полная производная по времени от вектора кинетического момента механической системы относительно некоторого неподвижного центра 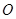 по величине и направлению равна главному моменту внешних сил, приложенных к механической системе, определенному относительно того же центра:

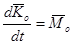 (3.1.2)

Здесь 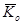 – кинетический момент механической системы относительно неподвижного центра 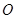; он является мерой движения системы вокруг этого центра и складывается из кинетических моментов всех точек и тел, входящих в эту систему;  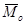– главный момент внешних сил относительно неподвижного центра .

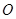Определим главный момент внешних сил:

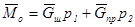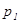, где  и 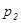 – плечи сил тяжести шарика и треугольника;

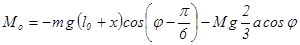 (3.1.3)

Определим кинетический момент системы. Он складывается из кинетических моментов шарика и треугольника: .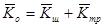

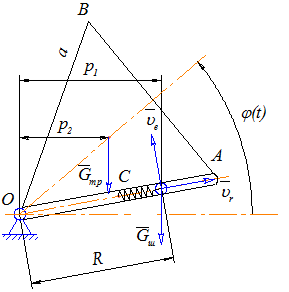
Рисунок 3.1.1. Составление уравнения движения твердого тела с помощью теоремы об изменении кинетического момента

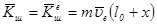, где модуль переносной скорости равен .

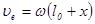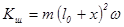 (3.1.4)

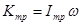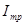,  – момент инерции треугольника  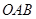относительно шарнира 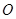. Определим его по теореме Штейнера:

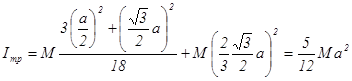 (3.1.5)

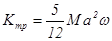 (3.1.6)

Учитывая (3.1.4) и (3.1.6), кинетический момент системы равен:

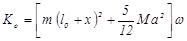 (3.1.7)

Продифференцируем выражение (3.1.7):

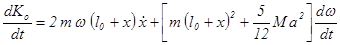 (3.1.8)

Подставив найденные значения в (3.1.2), теорема об изменении кинетического момента примет вид:

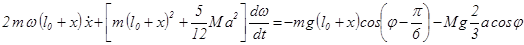 (3.1.9)