Оценка грубых погрешностей эксперимента.

Рсчётно-графическая работа

По предмету: Основы метрологии.

Тема: «Обработка результатов многократных измерений».

 

 

  Выполнил: студент ІІІ курса

 ФЭУ гр. МУ-321

Матузко А.В

Проверила: Гинергарт Оксана Юрьевна

 

 

Омск-2003

 

Содержание.

 

Введение

Исходные данные

 

Ι. Часть. Обработка результатов измерений.

ΙΙ. Часть. Проверка гипотезы об принятом законе распределения.

ΙΙΙ. Часть. Проверка гипотезы о принадлежности выборки к генеральной совокупности по критерию согласия Колмогорова.

 ΙV. Часть. Проверка гипотезы о независимости последовательности результатов измерений на уровне значимости α., используя критерии знаков и критерии Тренда. Критерий знаков

    V. Часть. Критерий Тренда.

VΙ. Часть. Оценка точности среднего.

VΙΙ. Часть. Оценка грубых погрешностей эксперимента.

 

Заключение

Список литературы

Приложение 1

Приложение 2

Приложение 3

 

Введение.

 

В науке и технике измерения занимают центральное место. Прогресс в этих областях зачастую связан с повышением их точности. Из-за неизбежных (от части исключаемых, но всё же имеющих место) погрешностей измеренное значение не соответствует в точности истинному значению. Чтобы результат измерения можно было далее использовать, необходимо указывать значения погрешностей измерений.

В зависимости от постановки задачи применяют различные параметры, характеризующие погрешность измерений. В физических и научных измерениях погрешность задаётся в виде параметра распределения случайной величены, в частности в виде среднего квадратического отклонения (СКО) генеральной совокупности.

 В технике, особенно при необходимости обеспечения взаимозаменяемости устройств, интерес представляет максимальное значение погрешности. Так как это значение не всегда можно указать, на практике довольствуются границами, которые с высокой вероятностью Р (например, Р=99%) не будет превышена. Это доверительная граница или погрешность измерений для вероятности Р.

Расчёт погрешности измерений проводится на основании обработки статистических данных, полученных на основе эксперимента или на основе эксплуатационных сведений и включает следующие этапы:

1. Построение вариационного ряда.

2. Построение эмпирической функции распределения и гистограммы.

3. Принятие решения о виде закона распределения случайной величены.

4. Расчёт величин оценок для математического ожидания и среднего квадратического отклонения.  

Исходные данные:

 

ВАРИАНТ №52

 

23,155668	23,16	23,261194	23,26	17,490901	17,49	20,006850	20,01
18,036949	18,04	19,953388	19,95	19,070663	19,07	20,509550	20,51
19,980613	19,98	19,639406	19,64	18,694913	18,70	19,835016	19,84
18,032346	18,03	14,734912	14,74	22,489878	22,48	15,617470	15,62
16,014493	16,01	19,967246	19,97	25,607984	25,61	22,516743	22,52
18,003079	18,00	22,755095	22,76	18,700127	18,70	16,962843	16,96
15,979836	15,97	21,478093	21,48	20,923235	20,92	17,184401	17,18
24,795771	24,80	21,258715	21,26	20,013455	20,01	18,677360	18,68
20,803856	20,80	20,271945	20,27	16,805881	16,81	18,040628	18,04
23,929105	23,93	17,675790	17,68	20,298695	20,30	17,407590	17,41
20,351977	20,35	21,730864	21,73	19,025735	19,03	17,219645	17,22
17,475253	17,48	17,763413	17,76	18,260862	18,26	21,950073	21,95
20,296301	20,30	17,053307	17,05	20,270393	20,27	16,009844	16,01
20,351370	20,35	22,617988	22,62	19,741223	19,74	22,765451	22,76
19,573814	19,57	18,798800	18,80	18,723656	18,72	21,609444	21,61
20,073228	20,07	18,676863	18,68	21,617009	21,62	16,069306	16,07
21,056400	21,06	13,050784	13,05	23,871371	23,87	20,255603	20,26
19,166575	19,17	15,121107	15,12	18,025055	18,02	19,507969	19,51
21,806718	21,81	19,999030	20,00	15,137427	15,14	19,975388	19,98
20,543405	20,54	18,135797	18,14	19,305864	19,31	19,115874	19,12
18,594111	18,59	20,338833	20,34	28,035200	28,04	14,123009	14,12
20,602122	20,60	23,847802	23,85	20,202482	20,20	26,834459	26,83
19,920718	19,92	23,597005	23,60	14,434317	14,43	19,210963	19,21
19,202480	19,20	16,021585	16,02	20,971719	20,97	21,227170	21,23
20,065173	20,06	19,285407	19,28	25,567098	25,57	20,989857	20,99

 

 

I. Часть.

Обработка результатов измерений.

 

 

Основная цель обработки экспериментальных данных –это получение результатов измерения и его погрешности.

Исходной информацией для обработки является ряд из n результатов измерений X₁ , X₂ , X₃ ……… ,X_n из которых исключены известные систематические погрешности, такой ряд называется выборкой.

 

 

1). Построение вариационного ряда X₁ < X₂ < X₃ …:

 

 

13,05	17,68	19,20	20,26	21,62
14,12	17,76	19,21	20,27	21,73
14,43	18,00	19,28	20,27	21,81
14,74	18,02	19,31	20,30	21,95
15,12	18,03	19,51	20,30	22,48
15,14	18,04	19,57	20,34	22,52
15,62	18,04	19,64	20,35	22,62
15,97	18,14	19,74	20,35	22,76
16,01	18,26	19,84	20,51	22,76
16,01	18,59	19,92	20,54	23,16
16,02	18,68	19,95	20,60	23,26
16,07	18,68	19,97	20,80	23,60
16,81	18,70	19,98	20,92	23,85
16,96	18,70	19,98	20,97	23,87
17,05	18,72	20,00	20,99	23,93
17,18	18,80	20,01	21,06	24,80
17,22	19,03	20,01	21,23	25,57
17,41	19,07	20,06	21,26	25,61
17,48	19,12	20,07	21,48	26,83
17,49	19,17	20,20	21,61	28,04

 

2). Определение широты распределения:

R=X_MAX-X_MIN;

 

R=28.04-13.05=14.99

 

3). Определяем возможное число разрядов:

q_MIN= 0.55*n^0.4=3.47≈3

 

    q_MAX =1.25* n^0.4 =7.88≈8

 

                         q=5

 

4). Определяем ширину интервала:

    ∆X=R / q;

        

    ∆X=14.99 / 5= 3.00

 

5). Расчёт границ интервалов:

∆₁ = (X_MIN; X₁+∆X)

    ∆₂ = (X₁+∆X; X₁+2∆X)

    ∆₃ = (X₁+2∆X; X₁+3∆X)

    ∆_n = (X_n+∆X; X_MAX)

 

    ∆₁ = (13,05; 16,05)

        

    ∆₂ = (16,05; 19,05)

 

    ∆₃ = (19,05; 22,05)

 

∆₄ = (22,05; 25,05)

 

    ∆₅ = (25,05; 28,05)

 

6). Подсчитываем частоты nj:

 

    nj₁ = 11

    nj₂ = 26

    nj₃ = 47

    nj₄ = 12

    nj₅ = 4

 

7). Расчёт середины интервалов Xjc:

    Xjc₁ = (13,05+16,05) / 2=14,55

    Xjc₂ = (16,05+19,05) / 2=17,55

    Xjc₃ = (19,05+22,05) / 2=20,55

    Xjc₄ = (22,05+25,05) / 2=23,55

    Xjc₅ = (25,05+28,05) / 2=26,55      

 

8). Вычисление среднего арифметического значения измеряемой величены:

 

__     m             X = 1    ∑ Xjc*nj ;                 n i =1

     

               

               

__                   X = 14,55*11+17,55*26+20,55*47+23,55*12+26,55*4 =19,71                                                         100

 

 

9). Вычисление отклонений середин интервалов от среднего арифметического и их квадратов:

               __

    Xjc – X ;

          __

    (Xjc – X)²;

 

    14,55-19,71= - 5,16

    17,55-19,71= - 2,16

    20,55-19,71=0,84

    23,55-19,71=3,84

    26,55-19,71=6,84;

 

    (14,55-19,71) ²=26,63

    (17,55-19,71) ²=4,67

    (20,55-19,71) ²=0,71

    (23,55-19,71) ²=14,75

(26,55-19,71) ²=46,79

 

10).       __

    (Xjc – X)²*nj;

 

    (14,55-19,71) ²*11=292,93

    (17,55-19,71) ²*26=121,42

    (20,55-19,71) ²*47=33,37

    (23,55-19,71) ²*12=177,00    

(26,55-19,71) ²*4=187,16

 

 

11). Вычисление дисперсии и среднего квадратического отклонения:

               

                  m

                     ∑                                     __

    Д_x = I=1 (Xjc – X)²*nj ;

                        n-1

                 

      Д_x = 292,93+121,42+33,37+177+187,16= 8,20 ;

                                         99                

        

    Среднее квадратическое отклонение:

 

    S_x =√ Д_x ;

 

    S_x =√8,20=2,86 ;

        

    Полученые оценки математического ожидания и СКО являются случайными. Рассеяние математического ожидания оцениваются с помощью среднего квадратического отклонения среднего арифметического: 

 

    S_x = S_x / √n ;

        

    S_x =2,86 / √100=0,286

 

J	Границы разрядов		Xjc	nj	Xjc*nj	Xjc-X	(Xjc – X)2	(Xjc – X)2*nj
	Xj	Xj+1
1	13,05	16,05	14,55	11	160,05	-5,16	26,63	292,93
2	16,05	19,05	17,55	26	456,30	-2,16	4,67	121,42
3	19,05	22,05	20,55	47	965,85	0,84	0,71	33,37
4	22,05	25,05	23,55	12	282,60	3,84	14,75	177,00
5	25,05	28,05	26,55	4	106,20	6,84	46,79	187,16

 

    ПОСТРОЕНИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ.

Смотри приложение 1.

 По виду построенной зависимости выдвигаем гипотезу о нормальном распределении.

 

                                                                        

 

 

II. Часть.

Проверка гипотезы о принятом законе распределения.

 

 

Для проверки закона распределения используют статистические характеристики, вычисленные в первом разделе в качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используют критерии согласия, наибольшее значение получил критерий Пирсона χ² . Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов построенные на основе распределения.

Этот метод можно использовать при n>50, у нас n=100.

       q

χ² =Σ (nj – npj)²

      j=1        npj

где:

nj и npj – соответственно экспериментальное и теоретическое значение частот в j-ом интервале разбиения.

    При n→∞ случайная величена χ² имеет распределение Пирсона с числом степеней свободы «К»; K= q – 1 – r;

    r – число определяемое по статистике параметров необходимых для совмещения моделей и частотограммы.  Для нормального закона распределения r=2.

        

    Методика определения соответствия экспериментального и принятого закона состоит в следующем:

     1). Определение: X, S_x , S_x

__

X=19,71; S_x = 2,86; S_x = 0,286.

 

    2). Группирование по разрядам ∆X (частотограмма).

∆₁ = (X_MIN; X₁+∆X)

    ∆₂ = (X₁+∆X; X₁+2∆X)

    ∆₃ = (X₁+2∆X; X₁+3∆X)

    ∆_n = (X_n+∆X; X_MAX)

 

∆₁ = (13,05; 16,05)

        

∆₂ = (16,05; 19,05)

 

∆₃ = (19,05; 22,05)

 

∆₄ = (22,05; 25,05)

 

∆₅ = (25,05; 28,05)

 

3). Подсчитываем для каждого разряда разбиения его середину Xjc и npj- число наблюдений теоретически соответствующие выбранной модели;

3.1). Xjc→tj то есть вычисляется аргумент дифференциальной функции нормированного распределения для каждого интервала.

                            __

tj = (Xjc – X) / S_x ;

 

tj₁=(14,55-19,71) / 2,86= -1,80 

    tj₂=(17,55-19,71) / 2,86= - 0,76

    tj₃=(20,55-19,71) / 2,86=0,29

    tj₄=(23,55-19,71) / 2,86=1,34

    tj₅=(26,55-19,71) / 2,86=2,39;

        

    3.2). По значению аргумента из таблицы находят значение функции плотности вероятности P(tj):

 

    P(tj)₁ = 0,0790

P(tj)₂ = 0,2989

P(tj)₃ = 0,3825

P(tj)₄ = 0,1626

P(tj)₅ = 0,0229

 

    3.3). Рассчитываем плотность вероятности физической величены в единицах этой величены.

 

    P(xj) = P(tj) / S_x ;

 

P(xj)₁ = 0,0790 / 2.86= 0,03

P(xj)₂ = 0,2989 / 2.86= 0,10

P(xj)₃ = 0,3825 / 2.86=0,13

P(xj)₄ = 0,1626 / 2.86=0,06

P(xj)₅ = 0,0229 / 2.86=0,01

 

 

    3.4). Рассчитываем теоретически частоты в каждом интервале.

 

    npj = n*∆x* P(xj);

        

    npj₁ =100*3.00*0,03=9

npj₂ =100*3.00*0,10=30

npj₃ =100*3.00*0,13=39

npj₄ =100*3.00*0,06=18

npj₅ =100*3.00*0,01=3

 

        

 

Если в какой-либо интервал попало меньше 5-и наблюдений, то в обеих гистограммах его соединяют с соседним интервалом.

    После этого определяют число степеней свободы:

 

     

K= q – 1 – r - m;

m- число укрупнений.

 

K=5-1-2-1=1

 

J	Xjc	nj	Xjc-X	tj	P(tj)	P(xj)	npj	χ2j
1	14,55	11	-5,16	-1,80	0,0790	0,03	9	0,44
2	17,55	26	-2,16	-0,76	0,2989	0,10	30	0,53
3	20,55	47	0,84	0,29	0,3825	0,13	39	1,64
4	23,55	16	3,84	1,34	0,1626	0,06	21	1,19
5	26,55		6,84	2,39	0,0229	0,01

 

4). Вычисление значения χ² по формуле.

      q

χ² =Σ (nj – npj)² ;

      j=1        npj

 

 

χ² = (11-9)²+(26-30)²+(47-39)²+(16-21)² = 109=1,10

                                99                      99    

 

 

5). По заданному уровню значимости α=0,1 и числу степеней свободы «К», находят граничные значения

 χ²_н (нижняя), χ²_в (верхняя)

χ²_н (K, α / 2=0,05)= а

χ²_в(K, 1- α /2=0,95)= в

 

χ²_н (1+0,05)=0,00393

χ²_в(1+0,95)=3,841

 

6). Сравниваем расчётные значения

 

χ²_н < χ² ≤χ²_в

          

0,004 < 1,10 < 3,84

 

Так как неравенство выполнятся, то гипотеза принимается.

ІІІ. Часть.

Проверка гипотезы о принадлежности выборки к генеральной совокупности по критерию согласия Колмогорова.

 

Согласно его критерию сравнивают эмпирические и теоретические значения интегральной функции распределения. Мерой расхождения между гипотезой и эмпирической функцией распределения является разность между эмпирической и гипотетической функциями распределения.

 

H=max | F̃(x)-F(x) |

 

Академик Колмогоров в 1933 г. доказал что, если функция F(x) не прирывна, то функция распределения величены λ равна произведению абсолютной величены наибольшей разности между соответствующими значениями эмпирической и теоретической функциями распределения непрерывной случайной величены X на корень квадратный из числа наблюдений.

 

λ = max | F̃(x)-F(x) |*√n;

при n→∞ функция распределения λ имеет пределом функцию:

     

 

+∞                               K(λ) = ∑ (-1)ke-2*k²*λ²          K=-∞

- Функция Колмогорова

 

Из определений предела и функций распределения случайной величены получаем, что при достаточно большом n и n>0 и вероятность того что:

P (H* √n< λ) ≈ K(λ)

Применение для проверки гипотезы о законе распределения случайной величены, сводится к нахождению величены «Н» и к нахождению величены λ

 

λ =H*√n

 

Ламбда задаётся для заданного уровня значимости α. Так как α=0,1 следовательно λ_α =1,22

Критерий Колмогорова применим в том случае,если известен не только вид функции, но и её параметры m_x и Sx         

   __ 

m_x = X

 

Определяя, принадлежит ли заданная выборочная совокупность к генеральной совокупности с параметрами m_x и Sx на уровне значимости α:

 

1). Строим ранжированный ряд:

 

13,05	17,68	19,20	20,26	21,62
14,12	17,76	19,21	20,27	21,73
14,43	18,00	19,28	20,27	21,81
14,74	18,02	19,31	20,30	21,95
15,12	18,03	19,51	20,30	22,48
15,14	18,04	19,57	20,34	22,52
15,62	18,04	19,64	20,35	22,62
15,97	18,14	19,74	20,35	22,76
16,01	18,26	19,84	20,51	22,76
16,01	18,59	19,92	20,54	23,16
16,02	18,68	19,95	20,60	23,26
16,07	18,68	19,97	20,80	23,60
16,81	18,70	19,98	20,92	23,85
16,96	18,70	19,98	20,97	23,87
17,05	18,72	20,00	20,99	23,93
17,18	18,80	20,01	21,06	24,80
17,22	19,03	20,01	21,23	25,57
17,41	19,07	20,06	21,26	25,61
17,48	19,12	20,07	21,48	26,83
17,49	19,17	20,20	21,61	28,04

 

2). Размах R:

 

R=X_MAX-X_MIN;

 

R=28.04-13.05=14.99

 

3). Количество интервалов q:

           q=5

 

4). Определяем: ∆X, nj, npj, P̃̃j =nj/n:

∆X=R / q;

        

    ∆X=14.99 / 5= 3.00;

 

nj₁ = 11

    nj₂ = 26

    nj₃ = 47

    nj₄ = 12

    nj₅ = 4;

                  

npj = n*∆x* P(xj);

        

    npj₁ =100*3.00*276.22=82866

npj₂ =100*3.00*1045.10=313530

npj₃ =100*3.00*1337.41=401223

npj₄ =100*3.00*568.53=170559

npj₅ =100*3.00*80.07=24021;

 

P̃̃̃j =nj/n:

 

P̃̃̃j₁ =11/100=0,11

P̃̃̃j₂ =26/100=0,26

P̃̃̃j₃ =47/100=0,47

P̃̃̃j₄ =12/100=0,12

P̃̃̃j₅ =4/100=0,04

 

5). Построение эмпирической функции распределения F̃(x)

 

F̃(x)₁ =0,11

F̃(x)₂ =0,37

F̃(x)₃ =0,84

F̃(x)₄ =0,96

F̃(x)₅ =1,00

 

6). Для определения гипотетической функции распределения:

а). Определим значение аргумента функции Лапласа, соответствующая правым границам всех интервалов:

 

Zj+1 =Xj+1 - m_x  ;

                      Sx

 

Zj+1₁ =16,05-19,71 = -1,28

               2,86

Zj+1₂ =19,05-19,71 = -0,23

              2,86

Zj+1₃ =22,05-19,71 =0,82

              2,86

Zj+1₄ =25,05-19,71 =1,87

              2,86

Zj+1₅ =28,05-19,71 =2,92

              2,86

 

б). Определение значения функции Лапласа по таблице Ф(z).

 

Ф(z)₁ = 3997= -0,3997

Ф(z)₂ = 0909= -0,0909

Ф(z)₃ = 2939=0,2939

Ф(z)₄ = 4693=0,4693

Ф(z)₅ = 4982=0,4982

 

в). Вычисление значения функции распределения F(x) предполагаемого в качестве теоретического закона распределения:

F(x)= 0,5+ Ф(z);

 

 

F(x)₁ =0,5-0,3997=0,10

F(x)₂ =0,5-0,0909=0,41

F(x)₃ =0,5+0,2939=0,79

F(x)₄ =0,5+0,4693=0,97

F(x)₅ =0,5+0,4982=1,00

 

7). Найти абсолютное значение разности между значениями эмпирической и теоретической функциями распределения при одинаковых значениях аргумента, а затем выбрать наибольшую из них.

 

H=max | F̃(x)-F(x) |

 

H₁ =0,11-0,10= 0,01

H₂ =0,37-0,41= 0,04

H₃ =0,84-0,79= 0,05

H₄ =0,96-0,97= 0,01

H₅ =1,00-1,00=0

 

    Н=0,05

 

8). Вычислить значение функции λ.

 

λ =H*√n;

 

λ=0,05*√100=0,5

 

9). По заданному уровню значимости определить значение λ_α

 

λ_α =1,22

 

10). Если λ ≤ λ_α то выдвинутая гипотеза о принадлежности выборки к генеральной совокупности считается справедливой.

 

0,5<1.22

Неравенство соблюдено.

 

J	Границы разрядов		nj	P̃̃̃j	F̃(x)	Zj+1	Ф(z)		F(x)		H
	Xj	Xj+1
1	13,05	16,05	11	0,11	0,11	-1,28	-0,40	0,10		0,01
2	16,05	19,05	26	0,26	0,37	-0,23	-0,09	0,41		0,04
3	19,05	22,05	47	0,47	0,84	0,82	0,29	0,79		0,05
4	22,05	25,05	12	0,12	0,96	1,87	0,47	0,97		0,01
5	25,05	28,05	4	0,04	1,00	2,92	0,50	1,00		0

 

ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ КРИВЫХ.

Смотри приложение 2.

ΙV. Часть.

 

Проверка гипотезы о независимости последовательности результатов измерений на уровне значимости α., используя критерии знаков и критерии Тренда.

 

Критерий знаков.

 

Пусть получено N результатов измерений случайной величены X. Критерий знаков заключается  в сравнении результатов измерений Xi величены X с некоторой величиной Me –медиана. Медиана –среднее число упорядоченного ряда то есть число, равно отстоящее от краёв. При чётном количестве членов медиана равна полу сумме средних значений. Если Xi>Me то «+», если Xi< Me то «-». Совокупность знаков последовательности «+» и «-», представляет собой серию τ_о . Число серий τ –случайная величена позволяет определить является ли результат данной последовательности измерений не зависимым.

При заданном уровне значимости проверка осуществляется путём сопоставления полученного числа серий τ с критическими точками τ_{верхнее}  и τ_нижнее.

 

 

ВАРИАНТ № 1а.

 

1). Строим из чисел ранжированный ряд.

 

0,06	0,7	1,57	2,4
0,37	0,81	1,59	2,49
0,41	0,91	1,69	2,68
0,57	1,15	1,92	2,8
0,59	1,43	2,06	3,08

 

2). Ищем медиану.

При чётном количестве членов медиана равна полу сумме средних значений.

Me = (1,43+1,57) / 2=1,5

3). Подсчитываем τ_о

0.41<1.5; 0.59<1.5; 0.70<1.5; 1.59>1.5; 2.68>1.5; 1.92>1.5; 3.08>1.5; 2.40>1.5; 1.57>1.5; 0.57<1.5; 0.91<1.5; 0.37<1.5; 1.43<1.5; 2.49>1.5; 1.69>1.5; 2.80>1.5; 2.06>1.5; 1.15<1.5; 0.06<1.5; 0.81<1.5.

- - - + + + + + + + - - - - + + + + - - -

τ_о =5

4). Ищем τ_н и τ_в, проверяем неравенство.

α.=0.1

τ_н (N, 1- α./2)=0.95

τ_в (N, α./2)=0,05

 

	Уровень значимости α.
Число изм. N	0,99	0,975	0,95	0,05	0,025	0,01
20	5	6	6	15	15	16

 

    τ_н < τ_о < τ_в

    6 > 5 < 15

Так как неравенство не выполняется, то гипотеза не принимается.

 

5). Строим график (Смотри приложение 3).
V. Часть.

Критерий Тренда.

 

Для последовательности N результатов измерений случайной величены X определяем число случаев, когда Xi>Xj где (i=1,2,3……N-1), (j=i+1,i+2……N)  i<j.

Каждое неравенство называется инверсией при этом:

                 

                    qij=         Xj>Xi – «1»   

                                              Xj<Xi – «0»  

 

Для i-го результата измерения инверсия равна:

   N

У_i =∑qij

    J=i+1

А общее число инверсии для всей последовательности результатов:

   N-1

У₀ =∑ У_i

    i=1

Если полученные результаты измерений являются независимыми то число инверсий, есть величена случайная имеющая распределения f(У). Для распределения инверсии составляется таблица критических точек в зависимости от уровня значимости α.

Критерий Тренда обладает наибольшей мощностью при выявлении систематических зависимостей носящих монотонно возрастающий или убывающий характер.

 

1). Считаем У_i

             N

У_i =∑qij

            J=i=1

0,41	1,92	0,91	2,80
0,59	3,08	0,37	2,06
0,70	2,40	1,43	1,15
1,59	1,57	2,49	0,06
2,68	0,57	1,69	0,81

 

У1 =2	У6 =9	У11 =3	У16 =4
У2 =3	У7 =13	У12 =1	У17 =3
У3 =3	У8 =10	У13 =3	У18 =2
У4 =8	У9 =7	У14 =5	У19 =0
У5 =13	У10 =2	У15 =3

2). Подсчитываем У₀

              N-1

У₀ =∑ У_i

              i=1

У₀ =2+3+3+8+13+9+13+10+7+2+3+1+3+5+3+4+3+2+0=94

3). Ищем У_н и У_в, проверяем неравенство.

α.=0.1

У_н (N, 1- α/2)=0,95

У_в (N, α/2)=0,05

 

	Уровень значимости α.
Число изм. N	0,99	0,975	0,95	0,05	0,025	0,01
20	59	64	69	120	125	130

У_н =69, У_в =120

У_н < У₀ < У_в

 

69< 94 <120

Так как неравенство выполняется, то гипотеза принимается.

VΙ. Часть.

Оценка точности среднего.

 

При заданном уровне значимости мерой точности определения математического ожидания является, величена доверительного интервала.

Для получения интервальной оценки нормального распределения случайной величены необходимо:

1). Определить точную оценку математического ожидания и среднее квадратическое отклонение X S_x :

 

S_x =√ Д_x ;

S_x =√8,20=2,86 ;

__     m         X = 1    ∑ Xjc*nj ;       n i =1

 __              

X = 19,71.

2). Определить доверительную вероятность:

 

P_Д =1- α =0,9 (90%)

 

3). Найти нижнюю и верхнюю границы интервала, где находится истинное значение оцениваемого параметра:

 

-Е= α/2; + Е=1- α/2.

α=0,1

 -Е=0,1 /2= -0,05

+ Е=1-0,1 /2= +0,95.

    Границы, определённые уровнем значимости называются доверительными границами, а интервал заключенный между доверительными границами называется доверительным интервалом. Площадь ограниченная доверительным интервалом и кривой плотности вероятности называется доверительной вероятностью.

 

    4). Для нормального распределения можно использовать связь с доверительным интервалом через доверительные границы:

    ±Е=Z*S _x ;

        

 

    5). Полученный доверительный интервал удовлетворяет условию:

 

=2Ф(Zp)

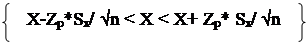Р

 

 

    где Z_p –аргумент функции Лопласа отвечающий вероятности Р/2.

 

6). Результат измерений записывается в виде:

Q=X± Z_p *S_x

    где Q –истинное значение измеряемой величены

Р=2Ф(Z_p )

Ф(Z_p )=0,45, тогда Z_p = 1,65

        

Q=19.71-1.65*0.286=19.24

Q=19.71+1.65*0.286=20.18

   

19,24< X < 20.18

VΙΙ. Часть.

Оценка грубых погрешностей эксперимента.

        

    Иногда при проведении анализа технологических процессов встречаются случаи, когда в результаты эксперимента вкрадывается грубая погрешность измерения.

    Грубая погрешность измерения может возникнуть в результате просчётов исследователя при измерении деталей, неправильного выбора измерительных баз, перекосов деталей, вибрации во время измерения.

Грубые погрешности измерения и обработки нередко оказывают решающее влияние на оценку точности технологических процессов и приводят к тому, что отдельные результаты наблюдений по своей величине значительно отличаются от других. Если исследователь убеждён, что такие наблюдения являются результатом ошибки, то эти наблюдения не следует учитывать при последующем анализе. Если же такой уверенности нет, то для определения того, являются ли резко выделяющиеся измерения результатом грубой ошибки или случайного отклонения, необходимо использовать определённые методы обнаружения грубых погрешностей.

 

Метод Романовского.

 

При этом методе на основе полученных опытных данных выборки вычисляют характеристики X и Sx, предварительно исключив из неё резко выделяющиеся значения Xi.

  Затем оределяют величену t_β по формуле

 

t_β = | Xi – X |

Sx

t_β = |28.04- 19.71| = 2.91

          2.86

Xi –наибольшее значение.

 

t_β´=2

Так как t_β > t_β´ , то Xi является грубой ошибкой и должно быть исключено из выборки.

Заключение.

 

В первой части расчётно-графической работы производилась обработка результатов измерений. В результате чего было получено следующее: Д_x (дисперсия) равна 8,20, а среднее квадратическое отклонение равно 2,86. Также для наглядности была построена гистограмма и график интегральной кривой.

Во второй части проверялась гипотеза о принятом законе распределения. В частности применялся критерий Пирсона χ². После всех проведённых вычислений оказалось, что данная гипотеза принимается так, как было выполнено неравенство χ²_н <χ² ≤χ²_в (0,004 < 1,10 < 3,84).

В третей части проверялась гипотеза о принадлежности выборки к генеральной совокупности по критерию согласия Колмогорова. В этой части для принятия гипотезы нужно было, чтобы выполнилось неравенство λ ≤ λ_α (0,5<1.22), поскольку условие выполнено, то гипотеза принемаенся. Также здесь для наглядности был построен график “Интегральные кривые”.

В четвёртой части проверялась гипотеза о независимости последовательности результатов измерений на уровне значимости α, используя критерий знаков. Эта гипотеза не была принятой , так как не было выполнено неравенство τ_н < τ_о < τ_в (6 > 5 < 15). Был построен график.

В пятой части проверялась гипотеза о независимости последовательности результатов измерений на уровне значимости α, используя критерий Тренда. Гипотеза была принятой поскольку неравенство выполнелось У_н < У₀ < У_в (69< 94 <120).