Методы прямоугольников

Курсовая работа

Тема: Разработка приложений на С, Pascal , Delphi

Оглавление

Оглавление

Введение

Глава 1. Нахождение значения интеграла с заданной точностью

1.1 Способы нахождения значения определённого интеграла

1.1.1 Методы прямоугольников

1.1.2 Метод трапеций

1.2 Программные средства языка C

1.2.1 Основы объектно-ориентированного программирования

1.2.2 Функции в C++

1.3 Программные средства языка Pascal (версия 7.0)

1.3.1 Объекты в Pascal

1.3.2 Оператор выбора в Pascal

1.4 Алгоритм программы вычисления определённого интеграла

1.5 Тестирование программы

Глава 2. Обработка результатов измерений

2.1 Теоретическая часть. Метод наименьших квадратов

2.2 Алгоритм программы обработки данных

2.3 Тестирование программы

Листинги программ

Вычисление интегралов С

Вычисление интегралов Pascal

Обработка измерений

Выводы

Список литературы

Приложение

Введение

Целью написания курсовой работы является обобщение практических знаний, полученных по курсу «Программирование на языках высокого уровня». Она содержит программные алгоритмы, которые служат для решения практических задач в области высшей математики и химии, написанные на языках, освоенных мной за время чтения курса: С++, Borland Pascal 7.0, Delphi 7.0.

В данной записке я поясняю теоретические основы использованных в курсовой работе языков программирования и некоторые теоретические основы математического анализа и химии, которые позволили мне разработать системные программы.

Глава 1. Нахождение значения интеграла с заданной точностью

Способы нахождения значения определённого интеграла

Численные методы основаны на замене интеграла

I=

конечной суммой

=

где  – числовые коэффициенты,  – точки отрезка [a; b], k=0, 1, …, n. Приближённое равенство ≈ , «называется квадратурной формулой, коэффициенты 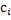 - коэффициентами квадратурной формулы,  - узлами квадратурной формулы» [5]. Отклонение от точно значения зависит от расположения узлов формулы, выбора коэффициентов и характера функции.

Методы прямоугольников

Методы прямоугольников основаны на представлении фигуры под графиком функции в виде ступенчатой фигуры, состоящей из прямоугольников. Отрезок интегрирования делится точками  на отрезки длиной = 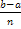. Затем получают значения функции в узлах формулы:  и считают значение сумм ( .

Отличие формул нахождения значения интеграла по методам левых, правых и средних прямоугольников состоит в том, в какой части отрезка ; ] считается значение : если в точке 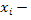метод левых прямоугольников, если в  – метод правых прямоугольников, если в середине отрезка – метод средних прямоугольников.

Метод трапеций

Данный метод состоит в аппроксимации графика функции прямой, проходящей через конечные значения. Площадь трапеции на отрезке ; ] вычисляется по формуле

= ( )

Тогда значение интеграла на этом отрезке вычисляется по формуле