 |
Главная |
Выполнил: студент гр. 462
|
из
5.00
|
Проверил: Веркиенко Ю. В.
2006 г.
Содержание
Цель работы
Задание
1. Генерирование выборок
2. Поиск оценок для выборок
3. Построение доверительных интервалов математического ожидания и дисперсии
4. Построение доверительного интервала для коэффициента корреляции
5. Построение эмпирической интегральной функции распределения и теоретической (для нормального закона с оценками среднего и дисперсии)
6. Построение эмпирической кривой плотности распределения и теоретической
7. Проверка гипотезы о величине среднего (), дисперсии (2), о нормальном законе распределения (по 2 и по Колмогорову)
8. Проверка гипотезы о независимости выборок и об одинаковой дисперсии в выборках
9. Составление системы условных уравнений и поиск по МНК оценки коэффициентов регрессии
10. Построение доверительных интервалов для коэффициентов регрессии, остаточной дисперсии и ошибок прогноза
11. Оценка значимости факторов по доверительным интервалам
Выводы
Цель работы
Выполнить все одиннадцать пунктов работы по заданию и сделать выводы.
Задание
На ЭВМ по программе случайных нормальных чисел с законом N(m,s2) генерировать две выборки объема n
x1,¼,xn (1)
y1,¼,yn (2)
Для выборок (1), (2) найти оценки 


 Ex, Sx,
Ex, Sx, 
 wx, wy.
wx, wy.
Для (1) построить доверительные интервалы для математического ожидания (считая s2 известной и неизвестной) и дисперсии.
Для (1), (2) построить доверительный интервал для коэффициента корреляции.
Для (1) построить эмпирическую интегральную функцию распределения  и теоретическую (для нормального закона с оценками среднего и дисперсии)
и теоретическую (для нормального закона с оценками среднего и дисперсии)
Для (1) построить эмпирическую кривую плотности распределения, разбив интервал (x(1), x(n)) на 5-6 интервалов. На этом же графике изобразить теоретическую кривую.
Проверить гипотезы: о величине среднего (m), дисперсии (s2), о нормальном законе распределения (по c2 и по Колмогорову).
Проверить гипотезу о независимости выборок (1), (2), об одинаковой дисперсии в выборках.
Для уравнения (модели)  с заданными коэффициентами bi составить систему условных уравнений, считая
с заданными коэффициентами bi составить систему условных уравнений, считая  и найти по МНК оценки коэффициентов регрессии. Значения брать из равномерного закона
и найти по МНК оценки коэффициентов регрессии. Значения брать из равномерного закона  или с равномерным шагом на отрезке [–1, 1].
или с равномерным шагом на отрезке [–1, 1].
Построить доверительные интервалы для коэффициентов регрессии, остаточной дисперсии и ошибок прогноза в точках x=-1, 0, 1.
По доверительным интервалам  оценить значимость факторов xi=xi. Фактор считается незначимым, если доверительный интервал накрывает значение, равное нулю.
оценить значимость факторов xi=xi. Фактор считается незначимым, если доверительный интервал накрывает значение, равное нулю.
При выполнении курсовой работы использовать значения: среднее выборок Х и У равно 3, дисперсия выборок равна 1. Уровень значимости a = 0.05. С.к.о. ошибки измерений в задаче регрессии 0.2.
1. Генерирование выборок
На ЭВМ по программе случайных нормальных чисел с законом N(m,s2) генерируем две выборки объема n = 17, где m = 3 и s2 = 1
x1,¼,xn (1)
y1,¼,yn (2)
Вариационные ряды:
 (1)
(1)  (2)
(2)
2. Поиск оценок для выборок
Для найденных выборок (1), (2) находим оценки 


 Ex, Sx,
Ex, Sx, 
 wx, wy.
wx, wy.
Выборочное среднее:


Квадрат средне – квадратичного отклонения:


Оценка центрального момента 3-го порядка:


Оценка центрального момента 4-го порядка:


Коэффициент эксцесса:


Коэффициент асимметрии:


Оценка корреляционного момента:


Оценка коэффициента корреляции:


Размах выборки:


3. Построение доверительных интервалов математического ожидания и дисперсии
Для (1) строим доверительные интервалы для математического ожидания (считая s2 известной и неизвестной) и дисперсии.
Считаем s2 известной.






Считаем s2 неизвестной.
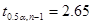





Таким образом, при различных вариантах μmin, μmax имеют почти одинаковые значения.

Подставляем табличные значения 24,7 и 5,01 в знаменатели подкоренного выражения и получаем, что
 ,
, 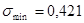
 ,
, 
4. Построение доверительного интервала для коэффициента корреляции
Для (1), (2) строим доверительный интервал для коэффициента корреляции.

U = 1,96
Так как  , то пусть
, то пусть  , отсюда z = 0,693
, отсюда z = 0,693

То есть |z| ≤ 0,693.
Если z = –0,693 и z = 0,693, то получим доверительный интервал для коэффициента корреляции –0,6 < Rxy < 0,6.
5. Построение эмпирической интегральной функции распределения и теоретической (для нормального закона с оценками среднего и дисперсии)
Создание ступенчатой функции, при скачке высотой 1/n.

Построение эмпирических Fx(u), Fy(u) и теоретических интегральных функций распределения. В последних средние и с. к. о. Взяты равными вычисленным оценкам математического ожидания и с. к. о.
Пусть u = 0, 0.001…6, тогда
 ,
, 

- - - - теоретическая функция распределения.
____ функция  для нормального закона с оценками среднего и дисперсии.
для нормального закона с оценками среднего и дисперсии.
6. Построение эмпирической кривой плотности распределения и теоретической
случайный выборка доверительный интервал
Для (1) построить эмпирическую кривую плотности распределения, разбив интервал (х(1),х(n)) на несколько подинтервалов. На этом же графике изобразить теоретическую кривую.
k*sigx - ширина интервалов разбиения, k - коэффициент шага разбиния. взято симметрично от среднего значения по 4 интервала
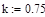







- - - - теоретическая функция плотности распределения.
____ эмпирическая кривая плотности распределения.
7. Проверка гипотезы о величине среднего (m), дисперсии (s2), о нормальном законе распределения (по c2 и по Колмогорову)
Проверка по критерию согласия  Пирсона:
Пирсона:
По данным выборки найдем теоретические частоты  , затем, сравнивая их с наблюдаемыми частотами
, затем, сравнивая их с наблюдаемыми частотами  , рассмотрим статистику
, рассмотрим статистику  - случайная физическая величина, имеющая распределение
- случайная физическая величина, имеющая распределение  с k степенями свободы. Если сумма
с k степенями свободы. Если сумма  , то выборочные данные согласуются с нормальным распределением и нет оснований отвергать нулевую гипотезу.
, то выборочные данные согласуются с нормальным распределением и нет оснований отвергать нулевую гипотезу.




Определим  с
с  степенями свободы:
степенями свободы:


Как видно условие  выполняется.
выполняется.
Проверка по критерию согласия Колмогорова:
Условие: 
где  , где
, где  максимальное значение разности между экспериментальным и теоретическим распределением нормального закона.
максимальное значение разности между экспериментальным и теоретическим распределением нормального закона.

 при
при 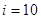 для X, и при
для X, и при  для Y.
для Y.

 - критическое значение квантиля распределения Колмогорова.
- критическое значение квантиля распределения Колмогорова.
Так как условие  – выполняется, то гипотеза о нормальном законе распределения подтверждена.
– выполняется, то гипотеза о нормальном законе распределения подтверждена.
8. Проверка гипотезы о независимости выборок и об одинаковой дисперсии в выборках
Чтобы из выборки х получить вариационный ряд необходимо осуществить 18 инверсий (т. е. Q=18).


Проверим гипотезу о независимости  :
: 
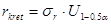
Так как  из нормального закона
из нормального закона  , то
, то 
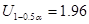




Так как условие  – выполняется, то выборки независимы.
– выполняется, то выборки независимы.
Теперь нам необходимо проверить гипотезу об одинаковой дисперсии в выборках
 :
: 







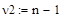

так как F<  ,то нет оснований, отвергать нулевую гипотезу.
,то нет оснований, отвергать нулевую гипотезу.
9. Составление системы условных уравнений и поиск по МНК оценки коэффициентов регрессии.
Для уравнения модели

Генерируем выборку с шагом
h = 1/N, где N = 100
Пусть даны коэффициенты регрессии:
β0 = 0; β1 = 1; β2 = 1; β3 = 0; β4 = 0; β5 = 1;
Значения матрицы плана






Сформируем элементы матрицы А вида:






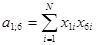

















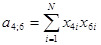
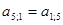
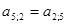
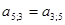
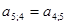









Формирование правых частей нормальной системы

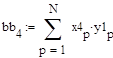





Где  случайная величина, сгенерированная по нормальному закону с учётом коэффициентов регрессии.
случайная величина, сгенерированная по нормальному закону с учётом коэффициентов регрессии.

Информационная матрица


Решение относительно коэффициентов регрессии.
Для нахождения вида уравнения регрессии необходимо вычислить коэффициенты регрессии  данного уравнения.
данного уравнения.


Уравнение регрессии :

Графики уравнения регрессии и результатов измерений, по которым определялись коэффициенты регрессии:

- - - - уравнение регрессии
____ случайная выборка из нормального закона
10. Построение доверительных интервалов для коэффициентов регрессии, остаточной дисперсии и ошибок прогноза
Доверительные интервалы будем находить для каждого элемента вектора оценок коэффициентов регрессии  .
.
В случае нормальных ошибок доверительные интервалы находятся из двойного неравенства:

где  - остаточная сумма квадратов;
- остаточная сумма квадратов;  - диагональный элемент ковариационной матрицы вида
- диагональный элемент ковариационной матрицы вида 
 так как слагаемых в уравнении регрессии шесть.
так как слагаемых в уравнении регрессии шесть.
 (1)
(1)
 (2)
(2)
 (3)
(3)
Строим интервал для коэф-та регрессии:



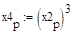
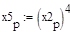





Доверительный интервал  , где из таблицы находим.
, где из таблицы находим.
k = 6;
Тогда для r = [1…6] будем
брать соответствующий элемент ковариационной матрицы, и находить доверительный интервал с учётом (1) (2) (3).
Нахождение доверительного интервала для  (фактор
(фактор  ):
):

- 
Нахождение доверительного интервала для  (фактор
(фактор  ):
):

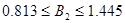
Нахождение доверительного интервала для  (фактор
(фактор  ):
):


Нахождение доверительного интервала для  (фактор
(фактор 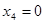 ):
):
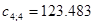

Нахождение доверительного интервала для  (фактор
(фактор  ):
):


Нахождение доверительного интервала для  (фактор
(фактор  ):
):


Доверительные интервалы для  ,
,  ,
,  не накрывают значение равное нулю, следовательно, факторы
не накрывают значение равное нулю, следовательно, факторы  ,
,  ,
,  являются значимыми, а факторы
являются значимыми, а факторы  ,
,  ,
,  - незначимыми.
- незначимыми.
11. Оценка значимости факторов по доверительным интервалам
Исключив из уравнения регрессии незначимые факторы, приходим к следующему виду:


Таким образом, из графика видно, что при исключении из уравнения регрессии незначимых факторов график не изменился. Найдем доверительный интервал для остаточной дисперсии
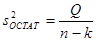 при
при 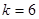 .
. 
А доверительный интервал найдём из следующего двойного неравенства:



Таким образом, доверительный интервал для остаточной дисперсии есть:





Выводы
Таким образом, в данной курсовой работе были изучены методы обработки случайных выборок с нормальным законом распределения. Так же найдены оценки коэффициентов регрессии и построены доверительные интервалы. В последнем пункте работы были оценены значимости факторов по доверительным интервалам.
|
из
5.00
|
Обсуждение в статье: Выполнил: студент гр. 462 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

