 |
Главная |
Линейный уравнение хорда гаусс ньютон
|
из
5.00
|
 ,
,  , если
, если 
 ,
,  , если
, если 
Погрешность вычислений:
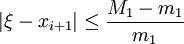 ,
,  ,
, 
В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала (рисунок 1).

| Рис. 1. Метод хорд | Рис.2. Метод касательных |
Здесь вычисляются значения функции на концах отрезка и строится “хорда”, соединяющая точки (a, f(a)) и (b, f(b)). Точка пересечения ее с осью абсцисс

принимается за очередное приближение к корню. Анализируя знак f(z) в сопоставлении со знаком f(x) на концах отрезка, сужаем интервал до [a,z] или [z,b] и продолжаем процесс построения хорд до тех пор, пока разница между очередными приближениями не окажется достаточно малой (в пределах допустимой погрешности) |Zn-Zn-1|<  .
.
Можно доказать, что истинная погрешность найденного приближения:
 ,
,
где X* - корень уравнения, Zn и Zn+1 - очередные приближения, m и M – наименьшее.
Метод Ньютона
Пусть корень уравнения  отделен на отрезке [a, b], причем
отделен на отрезке [a, b], причем  и
и  непрерывны и сохраняют определенные знаки при
непрерывны и сохраняют определенные знаки при  . Если на некотором произвольном шаге n найдено приближенное значение корня
. Если на некотором произвольном шаге n найдено приближенное значение корня  , то можно уточнить это значение по методу Ньютона. Положим
, то можно уточнить это значение по методу Ньютона. Положим
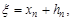
| (1) |
где 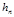 считаем малой величиной. Применяя формулу Тейлора, получим:
считаем малой величиной. Применяя формулу Тейлора, получим:

Следовательно,

Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня
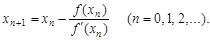
| (2) |
Геометрически метод Ньютона эквивалентен замене дуги кривой  касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что
касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что 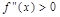 при
при  и
и  (см. рис.).
(см. рис.).
Выберем, например,  , для которого
, для которого  . Проведем касательную к кривой
. Проведем касательную к кривой  в точке B0 с координатами
в точке B0 с координатами  .
.

В качестве первого приближения 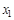 корня возьмем абсциссу точки пересечения касательной с осью Ox. Через точку
корня возьмем абсциссу точки пересечения касательной с осью Ox. Через точку  снова проведем касательную, абсцисса точки пересечения которой даст второе приближение
снова проведем касательную, абсцисса точки пересечения которой даст второе приближение  корня и т.д.
корня и т.д.
Формулу для уточнения корня можно получить из прямоугольного треугольника  , образованного касательной, проведенной в точке
, образованного касательной, проведенной в точке 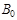 , осью абсцисс и перпендикуляром, восстановленным из точки
, осью абсцисс и перпендикуляром, восстановленным из точки  .
.
Имеем 
Так как угол образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е. 
 Тогда
Тогда 
или для любого шага n
 .
.
В качестве начальной точки  можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие
можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие

т.е. функция и ее вторая производная в точке  должны быть одного знака.
должны быть одного знака.
В качестве простейших условий окончания процедуры уточнения корня рекомендуется выполнение условия

Как следует из последнего неравенства, требуется при расчете запоминать три значения аргумента  . В практических инженерных расчетах часто применяют сравнение аргументов на текущей и предыдущей итерациях:
. В практических инженерных расчетах часто применяют сравнение аргументов на текущей и предыдущей итерациях:

При составлении программы решения уравнения методом Ньютона следует организовать многократный расчет приближений  для корня. Если удается получить аналитическое выражение для производной, то ее вычисление, а также вычисление
для корня. Если удается получить аналитическое выражение для производной, то ее вычисление, а также вычисление  можно оформить в виде функций.
можно оформить в виде функций.
|
из
5.00
|
Обсуждение в статье: Линейный уравнение хорда гаусс ньютон |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

