 |
Главная |
Проверка статистических гипотез для количества поступивших клиентов в систему (X).
|
из
5.00
|
Математические методы исследования экономики.
(системы массового обслуживания)
Выполнили: Аникин С.А. Проверил: Джафаров К.А.
Сердцев В.С. Дата
Студенты групп ФБЭ – 52, Оценка:
ФБЭ – 51
Дата 21.05.07
Новосибирск
2007г
Содержание:
1. Введение;………………………………………………………………………..стр. 3
2. Информация о рассматриваемой системе массового обслуживания (СМО); … …………………………………………………………………………………...стр. 4
3. Сводная таблица результатов по выборке;…………………………………...стр. 5
4. Проверка статистических гипотез (ПСГ) при помощи критерия «χ2» Пирсона:……………………………………………………………………..…..стр. 6
4.1. Проверка статистических гипотез для количества поступивших клиентов систему (X);
4.2. Проверка статистических гипотез для количества обслуженных клиентов системой (Y).
5. Расчёт показателей СМО;………………………………………………...…..стр. 13
6. Расчёт показателей СМО после улучшений, произведённых в системе;…стр. 15
7. Экономическая обоснованность улучшений;………………………….……стр. 19
8. Рекомендации по улучшению работы СМО;…………….…………….……стр. 21
9. Заключение;……………………………………………………………………стр. 22
10. Список используемой литературы;………………………………...………...стр. 23
Введение.
Данная работа представляет собой анализ системы массового обслуживания. В ней проводится расчёт основных показателей СМО, которые непосредственно влияют на её работу.
Целью данной расчётно-графической работы является получение теоретических и практических знаний и навыков по анализу систем массового обслуживания (на примере парикмахерской).
При проведении анализа были использованы элементы теории массового обслуживания, а так же элементы теории вероятностей и математической статистики.
|
Наименование организации: …
Род деятельности: парикмахерская
Место расположения: …
Контактный телефон: …
Время работы: с 9.00 до 20.00, без обеда и выходных
Необходимые данные для анализа системы:
Рассматриваемый промежуток времени:
с 19 марта 2007 по 27 апреля 2007г.
Рассматриваемый вид обслуживания:
стрижка
Рассматриваемое количество обслуживающих приборов:
2
Рассматриваемые дни:
дни с понедельника по пятницу включительно.
Рассматриваемый интервал времени:
11 часов (полное рабочее время).
3. Сводная таблица результатов по выборке.
| Рассматриваемый месяц | День месяца | Xi | Yi | Кол-во клиентов получивших отказ (U) | ||
| i | Кол-во поступивших клиентов | i | Кол-во обслуженных клиентов | |||
| Март | 19 | 1 | 32 | 1 | 22 | 10 |
| 20 | 2 | 40 | 2 | 30 | 10 | |
| 21 | 3 | 32 | 3 | 25 | 7 | |
| 22 | 4 | 31 | 4 | 22 | 9 | |
| 23 | 5 | 34 | 5 | 21 | 13 | |
| Март | 26 | 6 | 36 | 6 | 25 | 11 |
| 27 | 7 | 36 | 7 | 24 | 12 | |
| 28 | 8 | 32 | 8 | 24 | 8 | |
| 29 | 9 | 30 | 9 | 19 | 11 | |
| 30 | 10 | 36 | 10 | 26 | 10 | |
| Апрель | 2 | 11 | 31 | 11 | 22 | 9 |
| 3 | 12 | 27 | 12 | 17 | 10 | |
| 4 | 13 | 31 | 13 | 23 | 8 | |
| 5 | 14 | 32 | 14 | 21 | 11 | |
| 6 | 15 | 42 | 15 | 29 | 13 | |
| Апрель | 9 | 16 | 35 | 16 | 24 | 11 |
| 10 | 17 | 36 | 17 | 25 | 11 | |
| 11 | 18 | 26 | 18 | 17 | 9 | |
| 12 | 19 | 37 | 19 | 27 | 10 | |
| 13 | 20 | 33 | 20 | 23 | 10 | |
| Апрель | 16 | 21 | 33 | 21 | 23 | 10 |
| 17 | 22 | 40 | 22 | 29 | 11 | |
| 18 | 23 | 27 | 23 | 20 | 7 | |
| 19 | 24 | 32 | 24 | 21 | 11 | |
| 20 | 25 | 37 | 25 | 24 | 13 | |
| Апрель | 23 | 26 | 35 | 26 | 26 | 9 |
| 24 | 27 | 30 | 27 | 20 | 10 | |
| 25 | 28 | 23 | 28 | 17 | 6 | |
| 26 | 29 | 31 | 29 | 22 | 9 | |
| 27 | 30 | 39 | 30 | 25 | 14 | |
| Итого | -/- | -/- | 996 | -/- | 693 | 303 |
4. Проверка статистических гипотез (ПСГ) при помощи критерия «χ2» Пирсона.
Проверка статистических гипотез необходима для определения закона распределения генеральной совокупности, если этот закон нам заранее не известен.
Проверка статистических гипотез для количества поступивших клиентов в систему (X).
1. Формулируем гипотезы:
H0 – выборка из распределения Пуассона с параметрами λ и μ [F(x)=F0(x)].
H1 – выборка не из распределения Пуассона [F(x)≠F0(x)].
2. Выбираем уровень значимости критерия, необходимого для проверки гипотез:
α = 0,01
3. Выбираем статистику критерия, для этого рассчитаем значения параметров:
xi – количество поступивших клиентов в систему в i-тый день;
λ (  ) - среднее количество клиентов, поступивших в систему:
) - среднее количество клиентов, поступивших в систему:
ni – количество дней, соответствующее xi;
ni2 – количество дней, соответствующее xi, в квадрате;
Pi – вероятность свершения i-ого события;
Pk – вероятность того, что случайная величина X = k [Pk = P(x = k)];
χ2расч – расчётное значение критерия «χ2» Пирсона.
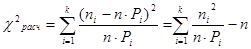 ,
,
 ,
,
 ,
,
 .
.
3.1 Строим таблицу для расчёта среднего значения:
Примечание: в данной и последующих проверках для получения среднего значения λ (  ) интервальные ряды не строились, поскольку нас интересуют точные значения среднего.
) интервальные ряды не строились, поскольку нас интересуют точные значения среднего.
Все расчёты проводились в ручном и машинном варианте, последний из которых представлен ниже (использованы средства Microsoft Excel 2003):
| Число единиц | Частоты (ni) | xi | xi*ni | |
| 1 | 23 | 1 | 23 | 23 |
| 2 | 26 | 1 | 26 | 26 |
| 3 | 27 | 2 | 27 | 54 |
| 4 | 30 | 2 | 30 | 60 |
| 5 | 31 | 4 | 31 | 124 |
| 6 | 32 | 5 | 32 | 160 |
| 7 | 33 | 2 | 33 | 66 |
| 8 | 34 | 1 | 34 | 34 |
| 9 | 35 | 2 | 35 | 70 |
| 10 | 36 | 4 | 36 | 144 |
| 11 | 37 | 2 | 37 | 74 |
| 12 | 39 | 1 | 39 | 39 |
| 13 | 40 | 2 | 40 | 80 |
| 14 | 42 | 1 | 42 | 42 |
Итого
30
996


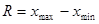 ,
, ,
,