Разные способы доказательства теоремы единственности

 

Преимущество предлагаемого второго доказательства заключается в том, что оно легко может быть перенесено на случай поверхностей F{x, у, z) = 0 (и даже на случай ( n -1) -мерных поверхностей второго порядка в n-мерном пространстве).

Обозначим через C множество точек, лежащих на кривой

F(x, у) = а₁₁х² + 2а₁₂ху + а₂₂у² + 2а₁х + 2а₂у + а₀ = 0 (6)

 

т. е. множество всех точек М=(х,у) комплексной плоскости, удовлетворяющих уравнению (6). Предположим, что множество С совпадает с множеством всех точек комплексной плоскости, удовлетворяющих уравнению

F(x, y) = b₁₁x² + 2b₁₂xy + b₂₂y² + 2b₁x + 2b₂y + b₀ = 0 (7)

 

Вспомним, что неасимптотические направления {α : β} по отношению к кривой (6) характеризуются тем, что имеется прямая данного направления {α : β} имеющая с множеством С ровно две (различные) общие точки, поэтому всякое направление, неасимптотическое для одной из двух кривых (6) и (7), будет неасимптотическим и для другой кривой.

Выбираем некоторое определенное неасимптотическое направление {α : β} для кривых (6) и (7).

Одну из прямых d направления {α : β} примем за ось ординат, а диаметр, сопряженный направлению {α : β}, — за ось абсцисс координатной системы О'х'у'. Из результатов предыдущего параграфа следует, что уравнения (3), (6) получат в системе координат О'х'у'

вид

F′(x′, y ′) = а′₂₂у′ ² + а′₁₁х′ ² + 2а′₁ x ′ + а′₀ =0 (8)

F′(x′, y′) = b′₂₂y′ ² + b′₁₁x′ ² + 2b′₁y′ + b′₀ = 0 (9)

 

Здесь a ′₂₂≠0 (и b ′₂₂≠0 ), в противном случае единичный вектор {0, 1} оси у', удовлетворяющий уравнению

φ′ (x′, y ′) = а′₁₁х′ ² + а′₂₂у′ ² = 0,

 

имел бы, вопреки предположению, асимптотическое направление. Пересечение множества С с осью у' = 0 обозначим через C ⁰. Возможны следующие случаи:

1° Множество С⁰ пусто. Этот случай осуществляется тогда и только тогда, когда какое-нибудь (и тогда каждое) из

f(x') = a′₁₁x′ ²+2a′₁x′+a′₀= 0

f (x') = b′₁₁x′ ²+2b′₁x′+b′₀= 0

противоречиво, т. е.

 

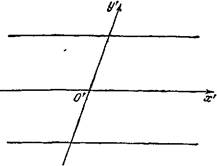
Множество C ⁰ пусто

 

Сногочленов f(x'), f(x') тождественно равен отличной от нуля постоянной а'₀, соответственно b ′₀.

2° Множество С⁰ совпадает со всей прямой у' = 0. Это происходит тогда и только тогда, когда каждый из многочленов f(x'), f(x') тождественно равен нулю.

 

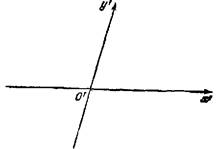
Множество C ⁰ совпадает с прямой y ′ o ′

 

3° Ни одни из случаев 1⁰, 2⁰ не имеет места. Тогда множество С⁰ состоит или из одной точки, или из пары (быть может, совпадающих между собою) точек, являющихся парой корней как уравнения

a ′₁₁ x ′ ²+2 a ′₁ x ′+ a ′₀= 0 (10)

 

так и уравнения

b ′₁₁ x ′ ²+2 b ′₁ x ′+ b ′₀= 0 (11)

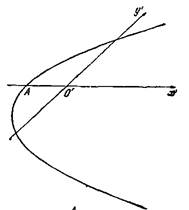
Множество C ⁰ состоит из одной точки А

Рассмотрим ближе этот случай. Так как уравнения (10) и (11) имеют одни и те же корни, то при некотором μ ≠ 0 имеем

b′₁₁x′ ²+2b′₁x′+b′₀ = μ (a′₁₁x′ ²+2a′₁x′+a′₀)

 

и, значит, полагая λ= b ′₂₂: a ′₂₂, имеем

F′(x′, y ′) = а′₂₂у′ ² + (а′₁₁х′ ² + 2а′₁ x ′ + а′₀),

F′(x′, y′) = λb′₂₂y′ ² + μ(b′₁₁x′ ² + 2b′₁y′ + b′₀)

 

Докажем, что λ = μ. Для этого дадим переменному х' значение x ′= x ′₁, являющаяся корнем уравнения

а′₁₁х′ ² + 2а′₁ x ′ + а′₀=1

 

и найдем значение y ′, удовлетворяющее уравнению

F′(x′₁, y ′) = а′₂₂у′ ² + 1 = 0

 

 

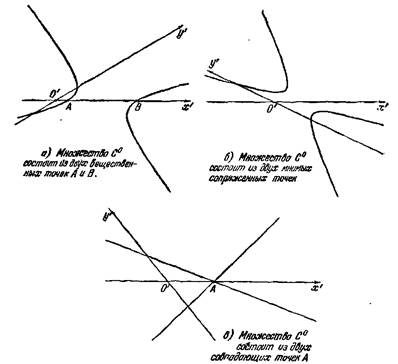
т. е. y ′₁= ± ( - 1 : a ′₂₂ )^0,5.

 

Значит, точка (x ′₁, y ′₁ ) принадлежит множеству С; следовательно,

F ′(x′₁, y ′₁) = λ а′₂₂у′ ² + μ · 1= λ а′₂₂( - 1 : a ′₂₂)+ μ = 0

т. е. λ=μ, и F′(x′, y ′)=λF′(x′, y ′), значит, и

F (x, y )=λF(x, y ).

Итак, в случае 3° теорема доказана. В случае 2° имеем

F′(x′, y ′)= а′₂₂у′ ², а′₂₂≠0, F′(x′, y ′)= b ′₂₂у′ ², b ′₂₂≠0.

 

Полагая λ = b ′₂₂: a ′₂₂, получим F′(x′, y ′)= F′(x′, y ′) —утверждение теоремы верно и в этом случае.

Наконец, в случае 1° уравнения (8) и (9) принимают вид

F′(x′, y ′) = а′₂₂у′ ² + a ′₀=0, a ′₀≠0,

F ′(x′, y ′) = b ′₂₂у′ ² + b ′₀=0 b ′₀≠0

 

— множество С есть пара прямых, определенная каждым из уравнений

y ′=±(-( a ′₀ : a ′₂₂)^0,5) или y ′=±(-( b ′₀ : b ′₂₂)^0,5).

 

Для того чтобы эти уравнения были эквивалентны, очевидно, необходимо и достаточно, чтобы было

(a′₀ : a′₂₂)=( b′₀ : b′₂₂), т.е. b′₂₂=λa′₂₂, b′₀=λa′₀ при λ =( b′₂₂: a′₂₂).

Теорема доказана во всех случаях.