 |
Главная |
Перечень условных обозначений
|
из
5.00
|
Содержание
Перечень условных обозначений
Введение
1 Факторизуемые группы с  -перестановочными подгруппами
-перестановочными подгруппами
2 Факторизуемые группы с  -перестановочными силовскими подгруппами
-перестановочными силовскими подгруппами
Заключение
Литература
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными. Используются обозначения, принятые в книгах. Буквами  обозначаются простые числа.
обозначаются простые числа.
Будем различать знак включения множеств  и знак строгого включения
и знак строгого включения  ;
;
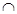 и
и  --- соответственно знаки пересечения и объединения множеств;
--- соответственно знаки пересечения и объединения множеств;
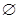 --- пустое множество;
--- пустое множество;
 --- множество всех
--- множество всех 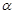 для которых выполняется условие
для которых выполняется условие  ;
;
 --- множество всех натуральных чисел;
--- множество всех натуральных чисел;
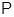 --- множество всех простых чисел;
--- множество всех простых чисел;
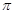 --- некоторое множество простых чисел, т.е.
--- некоторое множество простых чисел, т.е.  ;
;
 --- дополнение к
--- дополнение к 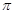 во множестве всех простых чисел; в частности,
во множестве всех простых чисел; в частности,  ;
;
примарное число --- любое число вида  ;
;
Пусть  --- группа. Тогда:
--- группа. Тогда:
 --- порядок группы
--- порядок группы  ;
;
 --- порядок элемента
--- порядок элемента  группы
группы  ;
;
 --- единичный элемент и единичная подгруппа группы
--- единичный элемент и единичная подгруппа группы  ;
;
 --- множество всех простых делителей порядка группы
--- множество всех простых делителей порядка группы  ;
;
 --- множество всех различных простых делителей натурального числа
--- множество всех различных простых делителей натурального числа  ;
;
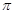 --группа --- группа
--группа --- группа  , для которой
, для которой  ;
;
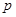 --группа --- группа
--группа --- группа  , для которой
, для которой  ;
;
 --- подгруппа Фраттини группы
--- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы
, т.е. пересечение всех максимальных подгрупп группы  ;
;
 --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы
, т.е. произведение всех нормальных нильпотентных подгрупп группы  ;
;
 --- наибольшая нормальная
--- наибольшая нормальная 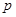 -нильпотентная подгруппа группы
-нильпотентная подгруппа группы  ;
;
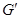 --- коммутант группы
--- коммутант группы  , т.е. подгруппа, порожденная коммутаторами всех элементов группы
, т.е. подгруппа, порожденная коммутаторами всех элементов группы  ;
;
 ---
---  -ый коммутант группы
-ый коммутант группы  ;
;
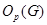 --- наибольшая нормальная
--- наибольшая нормальная 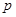 -подгруппа группы
-подгруппа группы  ;
;
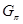 ---
--- 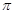 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 --- силовская
--- силовская 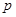 --подгруппа группы
--подгруппа группы  ;
;
 --- дополнение к силовской
--- дополнение к силовской 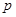 --подгруппе в группе
--подгруппе в группе  , т.е.
, т.е.  --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 --- группа всех автоморфизмов группы
--- группа всех автоморфизмов группы  ;
;
 ---
---  является подгруппой группы
является подгруппой группы  ;
;
 ---
---  является собственной подгруппой группы
является собственной подгруппой группы  ;
;
 ---
---  является максимальной подгруппой группы
является максимальной подгруппой группы  ;
;
нетривиальная подгруппа --- неединичная собственная подгруппа;
 ---
---  является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
 --- подгруппа
--- подгруппа  характеристична в группе
характеристична в группе  , т.е.
, т.е.  для любого автоморфизма
для любого автоморфизма  ;
;
 --- индекс подгруппы
--- индекс подгруппы  в группе
в группе  ;
;
 ;
;
 --- централизатор подгруппы
--- централизатор подгруппы  в группе
в группе  ;
;
 --- нормализатор подгруппы
--- нормализатор подгруппы  в группе
в группе  ;
;
 --- центр группы
--- центр группы  ;
;
 --- циклическая группа порядка
--- циклическая группа порядка  ;
;
 --- ядро подгруппы
--- ядро подгруппы  в группе
в группе  , т.е. пересечение всех подгрупп, сопряжённых с
, т.е. пересечение всех подгрупп, сопряжённых с  в
в  .
.
Если  и
и  --- подгруппы группы
--- подгруппы группы  , то:
, то:
 --- прямое произведение подгрупп
--- прямое произведение подгрупп  и
и  ;
;
 --- полупрямое произведение нормальной подгруппы
--- полупрямое произведение нормальной подгруппы  и подгруппы
и подгруппы  ;
;
 ---
---  и
и  изоморфны.
изоморфны.
Группа  называется:
называется:
примарной, если  ;
;
бипримарной, если  .
.
Скобки  применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
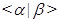 --- подгруппа, порожденная всеми
--- подгруппа, порожденная всеми 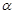 , для которых выполняется
, для которых выполняется  .
.
 , где
, где  .
.
Группу  называют:
называют:
 -замкнутой, если силовская
-замкнутой, если силовская  -подгруппа группы
-подгруппа группы  нормальна в
нормальна в  ;
;
 -нильпотентной, если
-нильпотентной, если  -холловская подгруппа группы
-холловская подгруппа группы  нормальна в
нормальна в  ;
;
 -разрешимой, если существует нормальный ряд, факторы которого либо
-разрешимой, если существует нормальный ряд, факторы которого либо 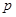 -группы, либо
-группы, либо  -группы;
-группы;
 -сверхразрешимой, если каждый ее главный фактор является либо
-сверхразрешимой, если каждый ее главный фактор является либо  -группой, либо циклической группой;
-группой, либо циклической группой;
нильпотентной, если все ее силовские подгруппы нормальны;
метанильпотентной, если существует нормальная нильпотентная подгруппа  группы
группы  такая, что
такая, что  нильпотентна.
нильпотентна.
разрешимой, если существует номер  такой, что
такой, что  ;
;
сверхразрешимой, если она обладает главным рядом, все индексы которого являются простыми числами.
Группа Шмидта --- это конечная ненильпотентная группа, все собственные группы которой нильпотентны.
Добавлением к подгруппе 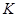 группы
группы  называется такая подгруппа
называется такая подгруппа  из
из  , что
, что  .
.
Минимальная нормальная подгруппа группы  --- неединичная нормальная подгруппа группы
--- неединичная нормальная подгруппа группы  , не содержащая собственных неединичных нормальных подгрупп группы
, не содержащая собственных неединичных нормальных подгрупп группы  .
.
Цоколь группы  --- произведение всех минимальных нормальных подгрупп группы
--- произведение всех минимальных нормальных подгрупп группы  .
.
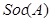 --- цоколь группы
--- цоколь группы  .
.
Экспонента группы  --- это наименьшее общее кратное порядков всех ее элементов.
--- это наименьшее общее кратное порядков всех ее элементов.
Цепь --- это совокупность вложенных друг в друга подгрупп. Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу.
Ряд подгрупп  называется:
называется:
субнормальным, если 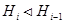 для любого
для любого  ;
;
нормальным, если  для любого
для любого  ;
;
главным, если 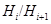 является минимальной нормальной подгруппой в
является минимальной нормальной подгруппой в  для всех
для всех  .
.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Также обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
 --- класс всех групп;
--- класс всех групп;
 --- класс всех абелевых групп;
--- класс всех абелевых групп;
 --- класс всех нильпотентных групп;
--- класс всех нильпотентных групп;
 --- класс всех разрешимых групп;
--- класс всех разрешимых групп;
 --- класс всех
--- класс всех  --групп;
--групп;
 --- класс всех сверхразрешимых групп;
--- класс всех сверхразрешимых групп;
 --- класс всех абелевых групп экспоненты, делящей
--- класс всех абелевых групп экспоненты, делящей  .
.
Формации --- это классы конечных групп, замкнутые относительно взятия гомоморфных образов и конечных подпрямых произведений.
Пусть  --- некоторый класс групп и
--- некоторый класс групп и  --- группа, тогда:
--- группа, тогда:
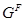 ---
---  --корадикал группы
--корадикал группы  , т.е. пересечение всех тех нормальных подгрупп
, т.е. пересечение всех тех нормальных подгрупп  из
из  , для которых
, для которых  . Если
. Если  --- формация, то
--- формация, то  является наименьшей нормальной подгруппой группы
является наименьшей нормальной подгруппой группы  , факторгруппа по которой принадлежит
, факторгруппа по которой принадлежит  . Если
. Если 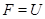 --- формация всех сверхразрешимых групп, то
--- формация всех сверхразрешимых групп, то  называется сверхразрешимым корадикалом группы
называется сверхразрешимым корадикалом группы  .
.
Формация  называется насыщенной, если всегда из
называется насыщенной, если всегда из  следует, что и
следует, что и  .
.
Класс групп  называется наследственным или замкнутым относительно подгрупп, если из того, что
называется наследственным или замкнутым относительно подгрупп, если из того, что 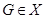 следует, что и каждая подгруппа группы
следует, что и каждая подгруппа группы  также принадлежит
также принадлежит  .
.
Произведение формаций  и
и  состоит из всех групп
состоит из всех групп  , для которых
, для которых  .
.
Введение
Понятие  -перестановочной подгруппы оказалось полезным инструментом в вопросах классификации непростых конечных групп. Отметим, в частности, что классическая теорема Холла о разрешимых группах на языке
-перестановочной подгруппы оказалось полезным инструментом в вопросах классификации непростых конечных групп. Отметим, в частности, что классическая теорема Холла о разрешимых группах на языке  -перестановочных подгрупп может быть сформулирована так: Группа
-перестановочных подгрупп может быть сформулирована так: Группа  разрешима тогда и только тогда, когда любые ее две силовские подгруппы
разрешима тогда и только тогда, когда любые ее две силовские подгруппы  -перестановочны. Согласно теореме 3.8 из группа
-перестановочны. Согласно теореме 3.8 из группа  является сверхразрешимой тогда и только тогда, когда все ее максимальные подгруппы
является сверхразрешимой тогда и только тогда, когда все ее максимальные подгруппы  -перестановочны со всеми другими подгруппами этой группы. Новые характеризации в терминах
-перестановочны со всеми другими подгруппами этой группы. Новые характеризации в терминах  -перестановочных подгрупп для класов разрешимых, сверхразрешимых и нильпотентных групп можно найти в работах . Целью данной главы является нахождение новых признаков сверхразрешимости группы на основе условий
-перестановочных подгрупп для класов разрешимых, сверхразрешимых и нильпотентных групп можно найти в работах . Целью данной главы является нахождение новых признаков сверхразрешимости группы на основе условий  -перестановочности некоторых ее подгрупп.
-перестановочности некоторых ее подгрупп.
1. Факторизуемые группы с  -перестановочными подгруппами
-перестановочными подгруппами
В данном разделе, развивая основные наблюдения работы, мы дадим новые критерии сверхразрешимости групп.
Пусть  --- группа и
--- группа и  --- ее подгруппа Фиттинга. Тогда
--- ее подгруппа Фиттинга. Тогда  является сверхразрешимой в том и только том случае, когда
является сверхразрешимой в том и только том случае, когда  , где
, где  и
и  --- такие сверхразрешимые подгруппы группы
--- такие сверхразрешимые подгруппы группы  , что каждая подгруппа группы
, что каждая подгруппа группы 
 -перестановочна с каждой подгруппой группы
-перестановочна с каждой подгруппой группы  .
.
Доказательство. Необходимость. Пусть  --- сверхразрешимая группа. Пусть
--- сверхразрешимая группа. Пусть  --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы  . Тогда
. Тогда 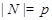 для некоторого простого числа
для некоторого простого числа  . Пусть
. Пусть  --- такая максимальная подгруппа группы
--- такая максимальная подгруппа группы  , что
, что  . Тогда
. Тогда  ,
,  и
и  сверхразрешимы и каждая подгруппа группы
сверхразрешимы и каждая подгруппа группы  перестановочна с каждой подгруппой группы
перестановочна с каждой подгруппой группы  .
.
Достаточность. Предположим, что  --- произведение сверхразрешимых подгрупп
--- произведение сверхразрешимых подгрупп  и
и  ,
,  --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  и каждая подгруппа группы
и каждая подгруппа группы 
 -перестановочна с каждой подгруппой группы
-перестановочна с каждой подгруппой группы  , но
, но  не является сверхразрешимой группой. Допустим, что
не является сверхразрешимой группой. Допустим, что  --- контрпример минимального порядка. Доказательство разобьем на следующие этапы.
--- контрпример минимального порядка. Доказательство разобьем на следующие этапы.
(1) Если  --- максимальная подгруппа группы
--- максимальная подгруппа группы  такая, что
такая, что  и либо
и либо  , либо
, либо  , то
, то  сверхразрешима.
сверхразрешима.
Предположим, что  . Тогда по тождеству Дедекинда имеем
. Тогда по тождеству Дедекинда имеем
 .
.
Так как

то каждая подгруппа группы 
 -перестановочна с каждой подгруппой группы
-перестановочна с каждой подгруппой группы  . Поскольку
. Поскольку  , то по выбору группы
, то по выбору группы  мы заключаем, что
мы заключаем, что  сверхразрешима.
сверхразрешима.
(2) Для любой неединичной нормальной в  подгруппы
подгруппы  факторгруппа
факторгруппа 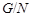 сверхразрешима.
сверхразрешима.
Ясно, что  . Пусть
. Пусть  и
и 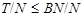 . Так как по условию для некоторого
. Так как по условию для некоторого  ,
,

то мы имеем



где 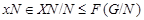 . Это показывает, что каждая подгруппа группы
. Это показывает, что каждая подгруппа группы 
 -перестановочна с каждой подгруппой группы
-перестановочна с каждой подгруппой группы  . Но поскольку
. Но поскольку 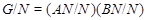 --- произведение сверхразрешимых подгрупп
--- произведение сверхразрешимых подгрупп  и
и  , то по выбору группы
, то по выбору группы  мы заключаем, что
мы заключаем, что  сверхразрешима.
сверхразрешима.
(3) Группа  имеет абелеву минимальную нормальную погруппу.
имеет абелеву минимальную нормальную погруппу.
Допустим, что  . Тогда ввиду (2),
. Тогда ввиду (2),  --- сверхразрешимая группа и поэтому
--- сверхразрешимая группа и поэтому  разрешима. Следовательно,
разрешима. Следовательно,  имеет абелеву минимальную нормальную погруппу.
имеет абелеву минимальную нормальную погруппу.
Предположим теперь, что 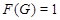 . Пусть
. Пусть  --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы  . Тогда по условию
. Тогда по условию  . Предположим, что
. Предположим, что  . Ввиду леммы мы видим, что
. Ввиду леммы мы видим, что 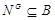 . Но
. Но  сверхразрешима, и поэтому минимальная нормальная подгруппа группы
сверхразрешима, и поэтому минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в  , абелева. Пусть теперь
, абелева. Пусть теперь 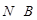 . Предположим, что
. Предположим, что  и пусть
и пусть  --- такая максимальная подгруппа группы
--- такая максимальная подгруппа группы  , что
, что  . Согласно (1),
. Согласно (1),  сверхразрешима, но
сверхразрешима, но 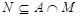 , и поэтому ввиду леммы ,
, и поэтому ввиду леммы ,  . Это показывает, что минимальная нормальная подгруппа группы
. Это показывает, что минимальная нормальная подгруппа группы  , которая содержится в
, которая содержится в  , абелева. Пусть теперь
, абелева. Пусть теперь 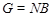 . Так как
. Так как 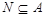 , то каждая подгруппа группы
, то каждая подгруппа группы  перестановочна с каждой погруппой группы
перестановочна с каждой погруппой группы  . Пусть
. Пусть  --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы  . Тогда
. Тогда  . Предположим, что
. Предположим, что  . Ввиду леммы мы видим, что
. Ввиду леммы мы видим, что  . Но
. Но  сверхразрешима, и поэтому минимальная нормальная подгруппа группы
сверхразрешима, и поэтому минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в  , абелева. Пусть теперь
, абелева. Пусть теперь  . Предположим, что
. Предположим, что  и пусть
и пусть  --- такая максимальная подгруппа группы
--- такая максимальная подгруппа группы  , что
, что 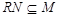 . Согласно (1),
. Согласно (1),  сверхразрешима, но
сверхразрешима, но 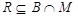 , и поэтому ввиду леммы ,
, и поэтому ввиду леммы , 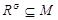 . Это показывает, что минимальная нормальная подгруппа группы
. Это показывает, что минимальная нормальная подгруппа группы  , которая содержится в
, которая содержится в  , абелева. Следовательно,
, абелева. Следовательно,  . Поскольку
. Поскольку 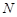 и
и  абелевы группы, то группа
абелевы группы, то группа  имеет абелеву минимальную нормальную подгруппу.
имеет абелеву минимальную нормальную подгруппу.
(4) Группа  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу 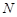 и
и  , где
, где  и
и  --- такая максимальная в
--- такая максимальная в  подгруппа, что
подгруппа, что
 и
и  .
.
Пусть  --- произвольная минимальная нормальная подгруппа группы
--- произвольная минимальная нормальная подгруппа группы  . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то
. Так как класс всех сверхразрешимых групп образует насыщенную формацию, то 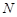 --- единственная минимальная нормальная подгруппа в
--- единственная минимальная нормальная подгруппа в  , причем
, причем  . Пусть
. Пусть  --- максимальная подгруппа в
--- максимальная подгруппа в  такая, что
такая, что  и пусть
и пусть  . Тогда по тождеству Дедекинда мы имеем
. Тогда по тождеству Дедекинда мы имеем  . Так как ввиду (3),
. Так как ввиду (3), 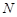 абелева, то
абелева, то  и
и 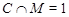 . Это показывает, что
. Это показывает, что  . Следовательно,
. Следовательно,  --- сверхразрешимая группа и ввиду леммы
--- сверхразрешимая группа и ввиду леммы  . Согласно (2) и выбора группы
. Согласно (2) и выбора группы  , мы имеем
, мы имеем 
(5)  --- наибольший простой делитель порядка группы
--- наибольший простой делитель порядка группы  .
.
Предположим, что  не является наибольшим простым делителем порядка группы
не является наибольшим простым делителем порядка группы  , и пусть
, и пусть  --- наибольший простой делитель
--- наибольший простой делитель 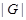 . Пусть
. Пусть 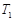 и
и  --- такие максимальные подгруппы группы
--- такие максимальные подгруппы группы  , что
, что  ,
,  . Тогда
. Тогда  . По лемме,
. По лемме, 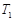 и
и  не сопряжены в
не сопряжены в  . Так как ввиду леммы все максимальные подгруппы группы
. Так как ввиду леммы все максимальные подгруппы группы  , которые не содержат
, которые не содержат  , сопряжены в
, сопряжены в  , то либо
, то либо  содержит
содержит 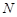 , либо
, либо  содержит
содержит  . Пусть, например,
. Пусть, например,  и пусть
и пусть 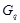 --- силовская
--- силовская  -подгруппа группы
-подгруппа группы  . Предположим, что
. Предположим, что 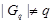 . Согласно (2),
. Согласно (2),  сверхразрешима и поскольку
сверхразрешима и поскольку  максимальная подгруппа группы
максимальная подгруппа группы  , то по лемме
, то по лемме  --- простое число. Значит,
--- простое число. Значит,  содержит неединичную силовскую
содержит неединичную силовскую  -подгруппу
-подгруппу  . Согласно лемме ,
. Согласно лемме ,  , и поэтому
, и поэтому  . Это противоречие показывает, что
. Это противоречие показывает, что 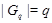 . Ясно, что
. Ясно, что 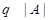 . Тогда
. Тогда  . Предположим, что
. Предположим, что  и пусть
и пусть  --- максимальная подгруппа группы
--- максимальная подгруппа группы  , содержащая
, содержащая  . Ввиду (1),
. Ввиду (1),  сверхразрешима. Без ограничения общности, мы можем предположить, что
сверхразрешима. Без ограничения общности, мы можем предположить, что 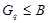 . Так как группа
. Так как группа  сверхразрешима, то
сверхразрешима, то  , и поэтому
, и поэтому  , что невозможно в силу (4). Значит,
, что невозможно в силу (4). Значит,  . Следовательно, по тождеству Дедекинда мы имеем
. Следовательно, по тождеству Дедекинда мы имеем

и поэтому  . Пусть
. Пусть 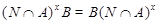 , где
, где  . Предположим, что
. Предположим, что  . Тогда
. Тогда  , и очевидно
, и очевидно  . Это влечет
. Это влечет  . Следовательно,
. Следовательно,  . Ясно, что
. Ясно, что  , и поэтому
, и поэтому 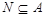 . Пусть
. Пусть  --- максимальная подгруппа группы
--- максимальная подгруппа группы  . Тогда для некоторого
. Тогда для некоторого  , мы имеем
, мы имеем 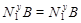 . Так как
. Так как  не является сверхразрешимой группой, то ввиду (4) мы видим, что
не является сверхразрешимой группой, то ввиду (4) мы видим, что  . Но поскольку
. Но поскольку  , то приходим к противоречию. Следовательно,
, то приходим к противоречию. Следовательно,  . Пусть
. Пусть 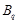 --- силовская
--- силовская 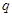 -подгруппа группы
-подгруппа группы  и для некоторого
и для некоторого  ,
,  . Предположим, что
. Предположим, что  . Пусть
. Пусть  --- максимальная подгруппа группы
--- максимальная подгруппа группы  , содержащая
, содержащая  . Согласно (1),
. Согласно (1),  сверхразрешима. Это влечет
сверхразрешима. Это влечет  , противоречие. Следовательно,
, противоречие. Следовательно,


