Обсчёт точки модифицированным методом Эйлера

Моделирование физических процессов

 

 

Екатеринбург 2009

Оглавление

Введение

Математическая модель

Описание теории применяемой к задаче

Блок – схемы

Листинг программы

Фотография графика

Решение задачи в MathCAD

Вывод

Литература

Введение

 

Благодаря данной курсовой работе, я получу основные навыки: в моделирование физических процессов, грамотного распределения информации и грамотного использования возможностей языка программирования Pascal.

Курсовая работа является первой объёмной самостоятельной работой для меня в роли программиста. Эта работа завершает подготовку по дисциплине “Программирование на языках высокого уровня” и становится базой для выполнения последующих курсовых проектов по специальным дисциплинам. После выполнения данной курсовой работы, я рассчитываю научиться строить графики функций, работать в MathCAD, и понимать геометрический смысл методов: Эйлера модифицированного и Рунге-Кутта.

Математическая модель, постановка задачи

1. Обсчитать первую точку методами Рунге – Кутта и Эйлера модифицированного.

2. Построить график к первой точке.

3. Составить блок - схемы.

4. Написать программу.

5. Построить график в MathCAD.

6. Сделать выводы

Описание теории применяемой к задаче

Метод Рунге – Кутта. Теория:

Пусть дано дифференциальное уравнение первого порядка

 

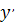 = f(x, y), с начальным условием y( ) = .

 

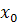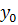Выберем шаг h и введём обозначения:

 

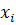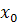 =  + i*h,  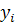= y( 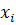), где

 i = 0, 1, 2, …

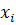 - узлы сетки,

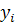 – значение интегральной функции в узлах.

Аналогично Модифицированного метода Эйлера решаем дифференциальное уравнение. Отличие состоит в делении шага на 4 части.

Согласно методу Рунге – Кутта 4 порядка, последовательные значения 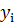 искомой функции y определяются по формуле:  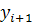=  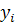+ ∆y, где

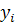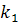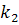∆  = ( + 2  + 2 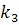 + 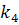), I = 0, 1, 2, …

 

А числа 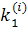, , 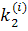,  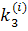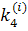на каждом шаге вычисляются по формулам:

 

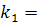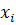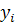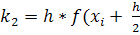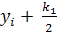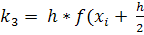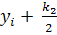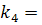h* f( , )

 

, )

 

, )

 

h* f( ,  + )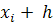

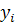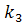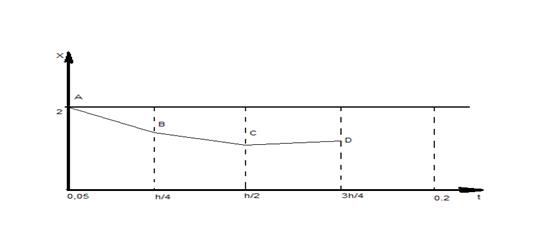
Обсчёт первой точки методом Рунге - Кутта:

Заданно уравнение движения материальной точки: 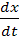 = x*sin(t), с условием

t 0 =1, t к =1.4, h = 0.05, x 0 =2. Необходимо построить физическую и математическую модель движения.

 

tg(a) = x*sin(t) = 2*sin(1)= 1.6829

/(a) = 1.0346

 

t(b) = 1.6829 + 0.125 = 1.8079

x(b) = 2+0.125*1.8079 = 2.2259

tg(b) = 2.2259*sin(1) = 1.8730

/(b) = 1.0803

 

t(c) = 1.6829 + 0.025 = 1.7079

x(c) = 2 + 0.025*(1.7079) = 2.0426

tg(c) = 2.0426*sin(1) = 1.7187

/(c) = 1.0438

 

t(d) = 1.6829 + 0.0375 = 1.7204

x(d) = 2 + 0.0375*1.7204 = 2.0645

tg(d) = 2.0645*sin(1) = 1.7372

/(d) = 1.0484

 

Метод Эйлера модифицированный

Теория:

Пусть дано дифференциальное уравнение первого порядка

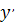 = f(x, y), с начальным условием y( ) = .

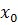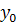Выберем шаг h и введём обозначения:

 

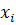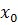 =  + i*h,  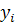= y( 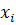), где

 i = 0, 1, 2, …

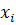 - узлы сетки,

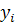 – значение интегральной функции в узлах.

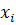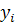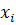1) Обозначим точки: A( , ), C( +h/2, 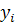+h/2*f( 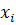, 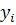)) и B( , ).

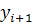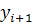2) Через точку A проведем прямою под углом a, где

Обсчёт точки модифицированным методом Эйлера

Заданно уравнение движения материальной точки: 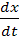 = x*sin(t), с условием

t 0 =1, t к =1.4, h = 0.05, x 0 =2. Необходимо построить физическую и математическую модель движения.

 

A(1; 2)

tg(a) = x*sin(t) = 2*sin(1)= 1.682

 

/(a) = 1.034

 

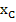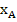 =  +  * f( , )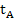

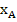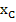 = 2 + 0.025*(1.6829) = 2.042

 

C(0.025; 2.042)

tg(c) = x*sin(t) = 2*sin(1.025) = 1.709

/(c) = 1.041

 

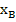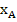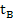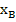= +h*f( + ; + *f( ; ))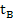

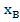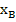 = 2 + 0.05*(1.041) = 2.05205

Листинг программы:

 

Uses crt,graph,graph0;

const

h=0.05;

var

gd,gm,n,i,j:integer;

a,b,k1,k2,k3,k4,d,g,c:real;

Xf:array[1..50] of integer;

Yf:array[1..50] of integer;

begin

clrscr;

a:=0;

b:=1.4;

n:=abs(round((a-b)/h));

readln;

writeln(' x= y= ');

writeln;

c:=2;

d:=0;

for j:=1 to n do

 begin

 k1:=h*c*sin(d);

 k2:=h*(c+0.5*k1)*sin(d+0.5*h);

 k3:=h*(c+0.5*k2)*sin(d+0.5*h);

 k4:=h*(c+k3)*sin(d+h);

 g:=k1+2*k2+2*k3+k4;

 

 Xf[j]:=round(100*d);

 Yf[j]:=round(100*c);

 if (j=1) or (j=2) or (j=3) or (j=4)

 or (j =5) or (j=6) or (j=7) or (j=8) or (j=9) then

 begin

 write(' ');

 write(j);write('. '); write(d);write(' ');writeln(c);

 delay(3000);

 end

 else

 begin

 write(j);write('. '); write(d);write(' ');writeln(c);

 delay(2000)

 end;

 d:=d+h;

 c:=c+g/6;

 end;

readln;

gd:=detect;

init('c:\tp70\bgi');

setbkcolor(15);

setcolor(3);

line(0,240,640,240);

line(320,0,320,480);

for i:=1 to n do

 begin

 if i+1<=n then

 begin

 setlinestyle(0,0,3);

 setcolor(7);

 line(320+Xf[i],Yf[i]-160,320+Xf[i+1],Yf[i+1]-160);

 putpixel(460,240,15);

 putpixel(320,40,15);

 putpixel(Xf[i]+320,Yf[i]-160,0);

 end;

 end;

readln;

closeGraph;

end.

Таблица измерений в Pascal, Mathcad:

t	X1	X2	Xm
2			2,077
2,1			2,16
2,2			2,247
2,3			2,341
2,4			2,44
2,5			2,545
2,6			2,656
2,7			2,773
2,8			2,896