 |
Главная |
Применение методов оптимизации для расчета БИХ-фильтров.
|
из
5.00
|
В последние годы широкое распространение получил другой класс методов расчета БИХ-фильтров, называемых методами оптимизации. Отличительной чертой этих методов является то, что система уравнений, составленная относительно коэффициентов фильтра, не может быть решена в явной форме. Поэтому для нахождения коэффициентов приходится использовать численные методы оптимизации, минимизирующие, согласно выбранному критерию, некоторую ошибку.
В качестве такого критерия используется критерий минимума среднеквадратической ошибки. При этом целевая функция задачи имеет вид
 ,
,
где  - (
- (  )-мерный вектор искомых коэффициентов,
)-мерный вектор искомых коэффициентов,  - получаемая амплитудная характеристика фильтра,
- получаемая амплитудная характеристика фильтра,  - заданная амплитудная характеристика фильтра,
- заданная амплитудная характеристика фильтра,  ,
,  - дискретный ряд частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра.
- дискретный ряд частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра.
Минимизация функции  сводится к нахождению оптимального значения параметрического вектора весовых коэффициентов фильтра
сводится к нахождению оптимального значения параметрического вектора весовых коэффициентов фильтра  . Так как функция
. Так как функция  является нелинейной, для ее минимизации необходимо использовать эффективные методы оптимизации.
является нелинейной, для ее минимизации необходимо использовать эффективные методы оптимизации.
При использовании методов оптимизации учитывается поведение только амплитудной характеристики, поэтому некоторые полюсы или нули после завершения итераций могут оказаться за пределами единичного круга. В этом случае можно прежде всего заменить полюс с полярными координатами  , оказавшийся вне единичного круга, на полюс с координатами
, оказавшийся вне единичного круга, на полюс с координатами  , находящийся внутри единичного круга. Амплитудная характеристика фильтра при такой замене остается неизменной, так как полюс заменяется своим зеркальным отображением. После того, как все полюсы оказываются внутри единичного круга, появляется возможность с помощью дополнительного анализа еще больше оптимизировать квадрат ошибки. Такая ситуация возникает достаточно часто, и в этих случаях оптимизация должна производиться двумя этапами:
, находящийся внутри единичного круга. Амплитудная характеристика фильтра при такой замене остается неизменной, так как полюс заменяется своим зеркальным отображением. После того, как все полюсы оказываются внутри единичного круга, появляется возможность с помощью дополнительного анализа еще больше оптимизировать квадрат ошибки. Такая ситуация возникает достаточно часто, и в этих случаях оптимизация должна производиться двумя этапами:
1. Использование программы оптимизации для минимизации функции  без каких-либо ограничений на расположение нулей и полюсов.
без каких-либо ограничений на расположение нулей и полюсов.
2. После завершения итераций инвертирование всех полюсов и нулей, оказавшихся вне единичного круга. После этого продолжение оптимизации для нахождения нового минимума  .
.
4. Описание метода синтеза фильтра
При разработке современных систем (в том числе и цифровых фильтров) возникает задача оптимального проектирования. Под этим термином понимается процесс разработки наилучшего, оптимального устройства (в каком-то смысле), как правило с помощью ЭВМ. Большинство методов оптимизации являются итерационными по своей природе.
Как было уже сказано, большинство методов оптимизации, в том числе и методов безусловной оптимизации, носит итерационный характер. Это значит, что начиная с какой-либо точки х0, называемой начальным приближением, алгоритм оптимизации генерирует последовательность точек х1, х2,…хn, которая в принципе должна сходиться к точке  . На практике процесс генерирования точек прекращается после конечного S числа шагов. И точка
. На практике процесс генерирования точек прекращается после конечного S числа шагов. И точка  выдается в качестве приближения к точке
выдается в качестве приближения к точке  . При этом вычисление очередной точки
. При этом вычисление очередной точки  называется к-той итерацией, а точку
называется к-той итерацией, а точку  - к-ым приближением.
- к-ым приближением.
Вектор 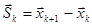 называется к-тым шагом. Отсюда
называется к-тым шагом. Отсюда  , к=0,1,2…
, к=0,1,2…
В основу всех методов оптимизации положено следующее правило: значение целевой функции от итерации к итерации должно убывать. То есть должно выполняться следующее условие:

Данное условие называется условием спуска.
Методы оптимизации, которые удовлетворяют этому условию, называются допустимыми или методами спуска. Основу всех методов спуска составляет следующая модельная схема:
1. к=0, выбирается начальное приближение 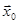 ;
;
2. Проверяются критерий останова. Если критерий выполняется, то расчеты прекращаются и точка  выдается как приближение
выдается как приближение  . В противном случае осуществляется переход к следующему пункту.
. В противном случае осуществляется переход к следующему пункту.
3. Рассчитывается ненулевой n-мерный вектор  , называемый направлением поиска или направлением шага.
, называемый направлением поиска или направлением шага.
4. Вычисляется малое положительное число  (длина шага) такое, что должно выполняться условие спуска:
(длина шага) такое, что должно выполняться условие спуска:

5. Выполнение к-той итерации  , к=к+1 и происходит переход к пункту 2.
, к=к+1 и происходит переход к пункту 2.
Шаг 4 в модельной схеме предполагает решение задачи одномерной минимизации – нахождение длины шага hk. Чтобы решить эту задачу, необходимо, чтобы вектор  был допустимым направлением поиска или направлением спуска, условием чего является следующее выражение :
был допустимым направлением поиска или направлением спуска, условием чего является следующее выражение : 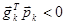 , то есть угол между вектором-градиентом и направлением поиска должен быть тупым.
, то есть угол между вектором-градиентом и направлением поиска должен быть тупым.
В модельной схеме значение целевой функции F(x) убывает от итерации к итерации. Тем не менее монотонно убывающая последовательность {F(x)} может не сойтись к минимуму по следующим причинам:
1. Как бы хорошо не выбиралось направление  , все может испортить неудачный выбор длины шага hk, при котором величина убывания целевой функции F(x) по итерациям будет слишком быстро стремиться к нулю.
, все может испортить неудачный выбор длины шага hk, при котором величина убывания целевой функции F(x) по итерациям будет слишком быстро стремиться к нулю.
2. Решение не удастся получить, если алгоритм расчета направления поиска  выдает векторы почти касательные к линиям уровня целевой функции, где ее значение постоянно. В результате угол между вектором-градиентом и направлением поиска будет стремиться к 90 градусам, то есть их скалярное произведение будет близким к нулю.
выдает векторы почти касательные к линиям уровня целевой функции, где ее значение постоянно. В результате угол между вектором-градиентом и направлением поиска будет стремиться к 90 градусам, то есть их скалярное произведение будет близким к нулю.
Следовательно, для того, чтобы получить гарантированно сходящуюся последовательность в соответствии с модельной схемой необходимо, чтобы длина шага hk обеспечивала бы существенное убывание целевой функции от итерации к итерации и, чтобы угол между вектором-градиентом и направлением поиска на каждой итерации был больше 90 градусов.
Помимо этих двух требований для обеспечения сходимости модельной схемы необходимо еще одно условие, которое накладывается на множество уровней целевой функции. Для функции F(x) и числа  множеством уровней называется совокупность всех точек, для которых справедливо выражение F(
множеством уровней называется совокупность всех точек, для которых справедливо выражение F(  )
) 
 . Дополнительное условие заключается в том, чтобы данное множество L(F(
. Дополнительное условие заключается в том, чтобы данное множество L(F( 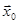 )) было бы ограничено и замкнуто.
)) было бы ограничено и замкнуто.
Таким образом, если
· функция F(x) непрерывна и дважды дифференцируема;
· ее множество уровней ограничено и замкнуто;
· функция F(x) существенно убывает от итерации к итерации и на каждом шаге угол между вектором-градиентом и направлением поиска всегда не равен 90 градусам на фиксированную положительную величину,
то алгоритм модельной схемы генерирует последовательность точек, для которых справедливо 
 .
.
Сходимость такого рода называется глобальной, так как она не предполагает близости начального приближения точки 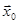 к стационарной точке
к стационарной точке  .
.
Четвертый шаг модельной схемы предполагает вычисление длины шага, то есть скалярной величины  , которая должна удовлетворять условию спуска:
, которая должна удовлетворять условию спуска:

Для того, чтобы выбрать  , удовлетворяющий этому условию, необходимо минимизировать значение целевой функции вдоль направления
, удовлетворяющий этому условию, необходимо минимизировать значение целевой функции вдоль направления  как функцию одной переменной (скалярной) h. То есть минимизировать функцию:
как функцию одной переменной (скалярной) h. То есть минимизировать функцию:

Чем точнее будет находиться минимум функции 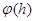 , тем быстрее будет сходиться алгоритм модельной схемы. С другой стороны очень точное нахождение минимума
, тем быстрее будет сходиться алгоритм модельной схемы. С другой стороны очень точное нахождение минимума  потребует больших вычислений функции, а следовательно вычисления целевой функции.
потребует больших вычислений функции, а следовательно вычисления целевой функции.
Для нахождения минимума  используются две группы методов одномерной оптимизации:
используются две группы методов одномерной оптимизации:
1. Эффективные методы одномерного поиска (метод Золотого сечения и метод Фибоначчи);
2. Методы полиномиальной интерполяции (Пауэлл, Ньютон, сплайн-интерполяция).
Для конкретизации модельной схемы помимо процедуры вычисления длины шага hk необходимо также задавать алгоритм расчета требуемого направления поиска  .
.
В отличие от одномерного случая, где возможно всего лишь два направления движения ( вперед и назад), уже в двумерной задаче множество направлений поиска является бесконечным.
В этом случае возникает проблема выбора направления поиска  . Именно способ вычисления
. Именно способ вычисления  и определяет «лицо» алгоритма безусловной минимизации. Поэтому названия алгоритмам оптимизации даются по реализованным в них процедурам вычисления
и определяет «лицо» алгоритма безусловной минимизации. Поэтому названия алгоритмам оптимизации даются по реализованным в них процедурам вычисления  .
.
В данной курсовой работе в качестве метода синтеза применяется метод сопряженных градиентов. В группе данных методов процедура вычисления направления поиска не предполагает решения каких либо СЛАУ. Эти методы принципиально отличаются от методов Ньютна и квазиньютоновских методов.
Рассмотрим задачу поиска минимума квадратичной функции вида:

с,G - вектор и полноопределенная матрица, независящие от вектора 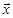 .
.
Предполагается, что нам известно к-тое приближение в точке минимума  и (к+1) линейно независимых векторов
и (к+1) линейно независимых векторов  .
.
Будем искать точку минимума целевой функции Ф(  ) на линейном множестве векторов
) на линейном множестве векторов  +
+  Рк, где Рк – (к+1)-мерное множество, образованное линейно независимыми векторами.
Рк, где Рк – (к+1)-мерное множество, образованное линейно независимыми векторами.
Множества, образованные вида  +
+  Рк называются линейными многообразиями.
Рк называются линейными многообразиями.
Задача сводится к нахождению точки минимума Ф(  ) на этом линейном многообразии.
) на этом линейном многообразии.
Для решения этой задачи сначала вводится матрица Рк=[  ]. Введение такой матрицы позволяет сформулировать задачу поиска минимума функции Ф(
]. Введение такой матрицы позволяет сформулировать задачу поиска минимума функции Ф( 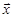 ) на многообразии
) на многообразии  +
+  Рк следующим образом: найти
Рк следующим образом: найти 
То есть надо найти вектор  , таким образом, чтобы точка
, таким образом, чтобы точка 
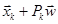 была бы точкой минимума функции
была бы точкой минимума функции  .
.
Для решения этой задачи необходимо сначала в функцию Ф(х) вместо 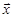
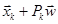 , затем продифференцировать получившуюся функцию по вектору
, затем продифференцировать получившуюся функцию по вектору  , приравнять результат к нулю и оттуда выразить вектор
, приравнять результат к нулю и оттуда выразить вектор 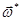 , который является решением задачи.
, который является решением задачи.
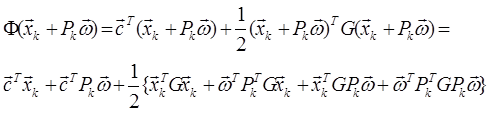

Если есть функция
 , то
, то 


Тогда точка минимума
 (1)
(1)
Формулу (1) можно рассматривать как формулу рекуррентного расчета точки  в классических методах спуска. Другими словами, формула (1) описывает процедуру пошаговой минимизации квадратичной функции Ф(х).
в классических методах спуска. Другими словами, формула (1) описывает процедуру пошаговой минимизации квадратичной функции Ф(х).
Формула (1) обладает рядом свойств:

 ,
,
то есть каждая компонента должна быть равна нулю
Так как предполагается, что все точки xj при j=1,к рассчитывается по формуле (1), то справедливо следующее свойство:
 i>j
i>j
Тогда формулу (1) можно преобразовать

ек – (к+1) столбец единичной матрицы
С учетом всего этого формула (1) примет вид
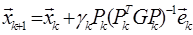

Последнее выражение можно упростить, если матрица  будет ортогональной. Ето возможно сделать, если вектора
будет ортогональной. Ето возможно сделать, если вектора 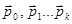 выбирать специальным образом. Вектора
выбирать специальным образом. Вектора 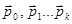 должны быть сопряженными относительно матрицы G, то есть должны выполняться следующие соотношения
должны быть сопряженными относительно матрицы G, то есть должны выполняться следующие соотношения

Тогда получаем упрощенное выражение

Таким образом мы установили, что среди методов минимизации квадратичных функций, укладывающихся в общую модельную схему, существует метод, к-тая итерация которого приводит в точку минимума функции Ф(  ) на многообразии
) на многообразии  +
+  Рк-1.
Рк-1.
Теоретически такой метод конечен, то есть он обеспечивает нахождение минимума функции Ф(  ) не более чем за N шагов (N-размерность задачи), так как многообразие
) не более чем за N шагов (N-размерность задачи), так как многообразие  +
+  Рк-1 на последнем N-том шаге совпадает с множеством значений аргумента
Рк-1 на последнем N-том шаге совпадает с множеством значений аргумента  и следовательно, если минимум функции Ф(
и следовательно, если минимум функции Ф(  ) не был найден ранее, то он обязательно будет найден на этом шаге.
) не был найден ранее, то он обязательно будет найден на этом шаге.
Для того, чтобы полностью определить метод сопряженных градиентов необходимо определить правило выбора вектора  . Это правило выглядит следующим образом:
. Это правило выглядит следующим образом:
 (2)
(2)
 - скаляр, который выбирается по двум теоретически эквивалентным формулам:
- скаляр, который выбирается по двум теоретически эквивалентным формулам:
1. 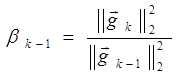 - формула Флетчера-Ривса
- формула Флетчера-Ривса
2.  - формула Полака-Рибьера
- формула Полака-Рибьера
Метод сопряженных градиентов для квадратических функций легко обобщается на случай целевой функции общего вида. Для этого необходимо ввести процедуру одномерного поиска длины шага hk и определиться, всегда ли направление поиска будет выдаваться по формуле (2) или допустимы отступления от нее. Такие отступления называются восстановлениями или рестартами. В начале рестарта вектор  . Метод сопряженных градиентов, использующий такие рестарты, называется традиционным. Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска. Он обладает теоретической N-шаговой сверхлинейной сходимостью, но из-за наличия ошибок округления реальная скорость сходимости метода сопряженных градиентов практически всегда линейна.
. Метод сопряженных градиентов, использующий такие рестарты, называется традиционным. Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска. Он обладает теоретической N-шаговой сверхлинейной сходимостью, но из-за наличия ошибок округления реальная скорость сходимости метода сопряженных градиентов практически всегда линейна.
Таким образом, хотя схема метода сопряженных градиентов далека от идеала, тем не менее этот метод остается единственным разумным средством для решения задачи оптимизации очень большой размерности (число переменных более 1000000).
5. Результаты синтеза
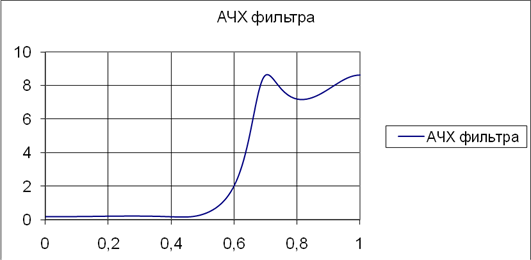
Синтез фильтра в данной курсовой работе был проведен на ЭВМ. В результате были получены следующие характеристики фильтра верхних частот третьего порядка:

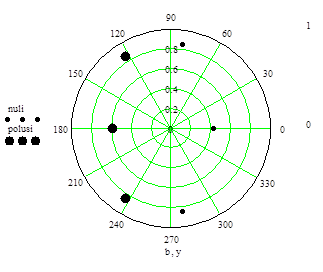
Устойчивость фильтра можно оценить по карте нулей и полюсов, полученных в результате синтеза фильтра:
| Нули | Полюсы | ||
| Модуль | Фаза | Модуль | Фаза |
| 0,4271382 | 0 | -0,5972885 | 0 |
| 0,8485097 | 82,4483 | 0,8551201 | 122,995 |
| 0,8485097 | -82,4483 | 0,8551201 | -122,995 |
Коэффициенты фильтра:
| ai | bi |
| -0.4271382 | 0.5972885 |
| -0.2230246 | 0.9313478 |
| 0.7199687 | 0.7312304 |
Заключение
В данной курсовой работе был рассчитан цифровой фильтр высоких частот 3-го порядка. Результаты расчета показали, что фильтр является устойчивым, поскольку нули и полюса фильтра лежат внутри единичной окружности, что иллюстрируется картой нулей и полюсов, а это является достаточным условием устойчивости цифрового фильтра. Также в работе представлены частотные характеристики, которые полностью удовлетворяют требованиям технического задания.
Список использованной литературы
1. Смирнов А.А. Лекции по курсу “Теория проектирования радиоэлектронных систем управления и передачи информации”, 2004г.
2. Езерский В.В. Лекции по курсу “Цифровая обработка сигналов и микропроцессоры в радиоуправлении”, 2003г.
3. Езерский В.В., Паршин В.С. Теоретические основы цифровой обработки сигналов: Учебное пособие. РГРТА, Рязань, 1996г.
|
из
5.00
|
Обсуждение в статье: Применение методов оптимизации для расчета БИХ-фильтров. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

