Свойства алгоритмов сжатия

Алгоритм RLE

В основу положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой, в которой указывается код данных и коэффициент повтора.

Например, для последовательности:

0; 0; 0; 125;125; 0; 248; 248; 248; 248 (всего 10 байтов)

1     2 3    4    5   6   7       8       9     10

Выявляются: значение и коэффициент повтора.

0 3

                               125                       2

0                         1

248 4

Новый вектор данных имеет вид:

0; 3; 125; 2; 0; 1; 248; 4 (всего 8 байтов) 

 

Коэффициент сжатия Kс=8/10*100%=80% или степень сжатия 10/8=1,25

 

Алгоритм отличается простотой, высокой скоростью работы, но обеспечивает недостаточное сжатие.

Наилучшими объектами для данного алгоритма являются графические файлы, в которых большие одноцветные участки изображения кодируются длинными последовательностями одинаковых байтов.

Этот метод может дать заметный выигрыш на некоторых типах файлов баз данных. Имеющих таблицы с фиксированной длиной полей.

Для текстовых данных методы RLE неэффективны.

В связи с этим большая эффективность алгоритма RLE достигается при сжатии графических данных (в особенности для однотонных изображений).

Пример сжатия серно-белого изображения

1 клетка 8 бит (Будем кодировать 0 – черный цвет – 8 бит, 1 – белый цвет – 8 бит), весь рисунок занимает памяти 8*64=512 бит

               Применяя сжатие                                                  Без сжатия

Для фигуры первая строка 1,8 = 2 байта                                           64 бита

               вторая строка 1,8 = 2 байта                                             64 бита                                                               

               третья строка 0,3+1,2+0,3 = 6 байт                               64 бита                                               

               четвертая строка 0,3+1,2+0,3 = 6 байт                          64 бита                                                                  

               пятая строка 0,3+1,2+0,3 = 6 байт                                 64 бита                                                                              

               шестая строка 0,3+1,2+1,3 = 6 байт                              64 бита                

               седьмая строка 1,8 = 2 байта                                          64 бита                                                                                       

               восьмая строка 1,8 =2 байта                                           64 бита                                                                                          

Объем рисунка до сжатия 8 строк*64бит=512 бит

Объем рисунка после сжатия 4*2+4*6=8+24=32 байта*8=256 бита

Кс=256*100/512 = 50%

№ строки	Vo исходного изображения, бит	Vсжатого 8-разрядного изображения
1	8*8=64	1,8=2 байт=16 бит
2	8*8=64	1,8=2 байт=16 бит
3	8*8=64	0,3+1,2+1,3 =6 байт=48 бит
4	8*8=64	0,3+1,2+1,3 =6 байт=48 бит
5	8*8=64	0,3+1,2+1,3 =6 байт=48 бит
6	8*8=64	0,3+1,2+1,3 =6 байт=48 бит
7	8*8=64	1,8=2 байт=16 бит
8	8*8=64	1,8=2 байт=16 бит
Итого	8*64=512 бит	4*16+4*48=64+192=256 бит

Кс=256*100/512 = 50%

Алгоритм KWE

В основу положен принцип кодирования лексических единиц исходного документа группами байтов фиксированной длины.

Лексическая единица – последовательность символов, справа и слева ограниченная пробелами или символами конца абзаца.

Лексической единицей может быть слово.

Результат кодирования сводится в таблицу, которая прикладывается к исходному коду и представляет собой словарь.

Для англоязычных текстов принято использовать двухбайтовую кодировку слов.

В русском языке много длинных слов, большое количество приставок, суффиксов и окончаний, поэтому не всегда удаётся ограничиться 2-х байтовыми словами. Образующиеся при этом пары байтов называют токенами.

Эффективность метода зависит от длины документа.

Из-за необходимости прикладывать к архиву словарь слов, длина кратких документов не только не уменьшается, но даже возрастает.

Алгоритм наиболее эффективен для англоязычных текстовых документов и файлов баз данных.

Пример сжатия текстовой фразы: «Мы изучаем информатику»

Лексическая единица	2-х байтовый код
Мы	0000000011111111
изучаем	0101010101010101
информатику	0011001100110011
пробел	0000000000000000

Объем фразы до сжатия 22 символа*8бит=176 бит

Объем фразы после сжатия 5 лексических единиц*16=80 бит (без словаря)

00000000111111110000000000000000010101010101010100000000000000000011001100110011

Кс=80*100/176 = 45,45%

Алгоритм Хаффмана

В основе алгоритма лежит кодирование не байтами, а битовыми группами.

Этот алгоритм кодирования информации был предложен Д.А. Хаффманом в 1952 году. Хаффмановское кодирование (сжатие) – это широко используемый метод сжатия, присваивающий символам алфавита коды переменной длины, основываясь на вероятностях появления этих символов.

Алгоритм Хаффмана основывается на том, что символы в тексте, как правило, встречаются с различной частотой.

При обычном кодировании мы каждый символ записываем в фиксированном количестве бит, например каждый символ в 1 байте, или в 2 байтах.

 Однако, т. к. некоторые символы встречаются чаще, а некоторые реже − можно записать часто встречающиеся символы в небольшом количестве бит, а для редко встречающихся символов использовать более длинные коды. Тогда суммарная длина закодированного текста может стать меньше.

Принцип кодирования:

· Перед началом кодирования производится частотный анализ кода документа с целью выявления частоты повтора каждого из встречающихся символов.

· Чем чаще встречается тот или иной символ, тем меньшим количеством битов он кодируется.

· Образующаяся в результате кодирования иерархическая структура, прикладывается к сжатому документу в качестве таблицы соответствия.

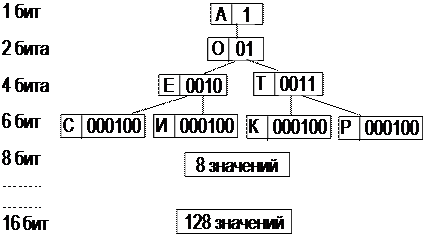
Соответственно, чем реже встречается символ, тем длиннее его кодовая битовая последовательность. Например:

 

 

 

       . . . . . . . . . . . . . .                  . . . . . . . . . . . . . . .    

 

       . . . . . . . . . . . . .                     . . . . . . . . . . . . . . .  

           

Используя 16 бит, можно закодировать до 256 различных символов. К сжатому архиву необходимо прикладывать таблицу соответствия, поэтому для файлов малых размеров алгоритм Хаффмана малоэффективен.

Эффективность алгоритма зависит и от заданной предельной длины кода (размера словаря). Наиболее эффективными оказываются архивы с размером словаря от 512 до 1024 единиц.

Все рассмотренные алгоритмы в «чистом виде» на практике не применяются, т.к. эффект каждого из них сильно зависит от начальных условий.

Идея алгоритма Хаффмана состоит в следующем: зная вероятности вхождения символов в исходный текст, можно описать процедуру построения кодов переменной длины, состоящих из целого количества  битов. Символам с большей вероятностью присваиваются более короткие коды. Таким образом, в этом методе при сжатии данных каждому символу присваивается оптимальный префиксный код, основанный на вероятности его появления в тексте.

Префиксный код – это код, в котором никакое кодовое слово не является префиксом любого другого кодового слова. Эти коды имеют переменную длину.

Оптимальный префиксный код – это префиксный код, имеющий минимальную среднюю длину.

Реализацию Алгоритма Хаффмана можно разделить на два этапа:

1. Определение вероятности появления символов в исходном тексте.

Первоначально необходимо прочитать исходный текст полностью и подсчитать вероятности появления символов в нем (иногда подсчитывают, сколько раз встречается каждый символ). Если при этом учитываются все 256 символов, то не будет разницы в сжатии текстового или файла иного формата.

2. Нахождение оптимального префиксного кода.

Коды Хаффмана имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину.

Алгоритм построения дерева Хаффмана.

Шаг 1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо по числу появления символа в сжимаемом тексте.

Шаг 2. Выбираются два свободных узла дерева с наименьшими весами.

Шаг 3. Создается их родитель с весом, равным их суммарному весу.

Шаг 4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.

Шаг 5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой – бит 0.

Шаг 6. Повторяются шаги, начиная со второго, до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Существует два подхода к построению кодового дерева: от корня к листьям и от листьев к корню.

Пример построения кодового дерева.

Пусть задана исходная последовательность символов:

2     8     4 1 5        Количество повторений символов

aabbbbbbbbccсcdeeeee.

Ее исходный объем равен 20 байт (20*8=160 бит).

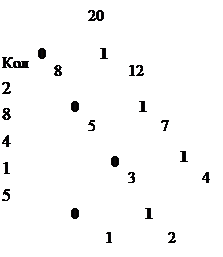
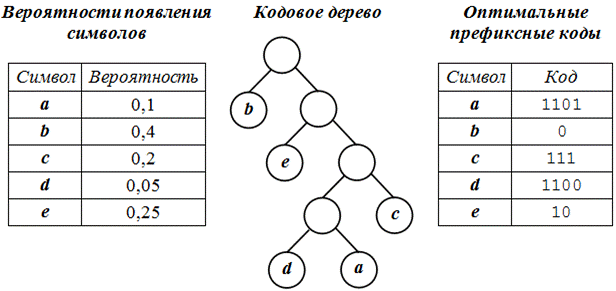
                                Создание оптимальных префиксных кодов

В соответствии с приведенными на рисунке данными (таблица вероятности появления символов, кодовое дерево и таблица оптимальных префиксных кодов) закодированная исходная последовательность символов будет выглядеть следующим образом:

a a bb bb bb bb c c c c d e e e e e

110111010000000011111111111111001010101010.

Следовательно, ее объем будет равен 42 бита. Степень сжатия приближенно равен 20*8/42=160/42=3,8.

Классический алгоритм Хаффмана имеет один существенный недостаток. Для восстановления содержимого сжатого текста при декодировании необходимо знать таблицу частот, которую использовали при кодировании. Следовательно, длина сжатого текста увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию данных. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по тексту: одного для построения модели текста (таблицы частот и дерева Хаффмана), другого для собственно кодирования.

Свойства алгоритмов сжатия

Алгоритм	Выходная структура	Сфера применения	Примечание
RLE (Run-Length Encoding	Список (вектор данных)	Графические данные	Эффективность алгоритма не зависит от объема данных
KWE (Keyword Encoding)	Таблица данных (словарь)	Текстовые данные	Эффективен для массивов большого объема
Алгоритм Хаффмана	Иерархическая структура (дерево кодировки)	Любые данные	Эффективен для массивов большого объема