Способы реализации ЦОС

Предельные циклы

Ошибки округления при вычислениях в цифровых фильтрах могут приводить к еще одной очень серьезной неприятности — появлению так называемых предельных циклов (limit cycle), когда вроде бы устойчивый фильтр начинает демонстрировать неустойчивое поведение.

Поясним это явление на простейшем примере. Пусть имеется рекурсивный фильтр первого порядка, описываемый разностным уравнением

y(k) = x(k) + 0,95 y(k – 1).

Единственный полюс функции передачи данного фильтра, равный 0,95, находится внутри единичной окружности, что свидетельствует об устойчивости фильтра.

Пусть входной сигнал отсутствует (x(k) = 0), а внутреннее состояние фильтра, которое в данном случае представляется единственным числом y(0), равно 13. При точных вычислениях сигнал на выходе фильтра экспоненциально затухает:

y(1) = 0,95 y(0) = 0,95 ⋅ 13 = 12,35,

y(2) = 0,95 y(1) = 0,95 ⋅ 12,35 = 11,7325,

y(3) = 0,95 y(2) = 0,95 ⋅ 11,7325 = 11,145875,

y(4) = 0,95 y(3) = 0,95 ⋅ 11,145875 = 10,58858125,

y(5) = 0,95 y(4) = 0,95 ⋅ 10,58858125 = 10,0591521875,

А теперь будем считать, что в ячейке памяти фильтра значение хранится в целочисленном формате и после выполнения умножения используется округление (будем обозначать его квадратными скобками). Выходной сигнал радикально изменится:

y(1) = [0,95 y(0)] = [0,95 ⋅ 13] = [12,35] = 12,

y(2) = [0,95 y(1)] = [0,95 ⋅ 12] = [11,4] = 11,

y(3) = [0,95 y(2)] = [0,95 ⋅ 11] = [10,45] = 10,

y(4) = [0,95 y(3)] = [0,95 ⋅ 10] = [9,5] = 10,

y(5) = [0,95 y(4)] = [0,95 ⋅ 10] = [9,5] = 10

Итак, выходной сигнал фильтра "залипает" на значении 10 и далее не меняется. Это и есть простейший случай предельного цикла (с периодом, равным единице).

Если в разностном уравнении фильтра изменить знак у коэффициента 0,95, мы получим предельный цикл с периодом, равным двум, в виде чередования значений 10 и –10. В фильтрах более высокого порядка могут возникать предельные циклы с разным периодом.

Имеются две разновидности предельных циклов:

предельные циклы низкого уровня (granular limit cycle) возникают, когда значения внутреннего состояния фильтра при отсутствии входного сигнала затухают, но из-за ошибок округления не доходят до нуля. Именно такой цикл наблюдается в приведенном примере;

предельные циклы высокого уровня (overflow limit cycle) имеют место в том случае, когда из-за вычислительных погрешностей значения внутреннего состояния фильтра при отсутствии входного сигнала не затухают, а возрастают, вызывая переполнение.

Способы реализации ЦОС

Среди алгоритмов ЦОС можно выделить как простые алгоритмы, так и сложные. Тем не менее, не смотря на сложность алгоритма, вычисления выполняются при помощи базовых операций: сложения, вычитания, умножения.

Возведение в степень – это многократное умножение, а деление – многократное вычитание, причем частное может быть как целым, так и дробным числом, поэтому при реализации деления необходимо задавать требуемую точность вычислений.

Так как вычислительные операции проводятся с данными, задержанными друг относительно друга на один и более периодов дискретизации с помощью элементов задержки, то требуется иметь возможность осуществлять пересылки и сдвиги данных. Так же для управления вычислительным процессом необходимо иметь логические операции.

Достаточно перечисленного для реализации алгоритма ЦОС? Достаточно.

В математической логике доказывается, что алгоритм любой сложности может быть построен и вычислен с использованием конечного числа простейших математических и логических операций, а так же операций сдвига и пересылки. Вычисление одного отсчета выходной последовательности может осуществляться за ограниченное число шагов.

Сама процедура вычисления может или выполняться никогда не останавливаясь, или по какой-то причине прерваться на каком-либо шаге, прекратить текущие вычисления и обратиться к другому алгоритму. Такое обращение называют прерыванием, а сигнал, вызвавшим прерывание, называют запросом на прерывание.

Принципиальная возможность вычислимости того или иного алгоритма еще не означает, что требуемое число шагов вычислений удовлетворяет практическим нуждам. Важнейшим фактором, определяющим пригодность реализованного алгоритма, является время вычисления одного отсчета (с заданной точностью)

Таким образом, определяющим свойством реализации алгоритма ЦОС является ее практическая вычислимость, т.е. способность вычислять отсчет с заданной точностью за разумное время (принято говорить реальное время)

Реальное время

Определение реального времени зависит от объема вычислений, точности вычислений, частотой дискретизации. Говорят, что система работает в реальном времени, если время выполнения алгоритма не превышает периода дискретизации

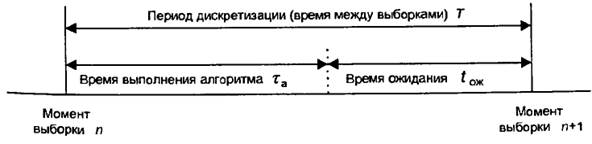
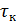 – время выполнения элементарной команды,  – число командных циклов

Время выполнения алгоритма зависит от способа реализации алгоритма ЦОС. Существуют три способа:

- Аппаратный

- Программный

- Аппаратно-программный

Аппаратная реализация предусматривает использование разнообразных функциональных блоков: регистров, сумматоров, шифраторов, умножителей, сдвигателей, логических элементов и т.д. Совокупность функциональных блоков и связей между ними определяет реализуемый алгоритм ЦОС.

Рассмотрим пример

Из структурной схемы алгоритма следует, что цифровое устройство, реализующее данный алгоритм, должно иметь:

- память коэффициентов, память исходных и промежуточных данных

- систему ввода и вывода исходных данных и результата

- умножители

- сумматор

- генератор тактовой частоты с периодом следования импульсов

Такое цифровое устройство изображено на рисунке:

Вместо нескольких умножителей используется один быстродействующий умножитель, на один вход которого последовательно, согласно логике вычислений, поступают данные x(n) и y(n), на другой – соответствующие коэффициенты. Получаемые произведения подаются в накапливающий сумматор, с выхода которого данные считываются один раз в период дискретизации

Вместо линий задержек обычно используют память входных и выходных данных, а так же память коэффициентов. По окончании вычислений очередного отсчета y(n) осуществляется его пересылка в память выходных данных, откуда подается на устройство вывода.

В памяти входных и выходных данных происходит сдвиг данных, что означает готовность устройства к приему очередного отсчета входных данных. Ответственным за последовательностью выполнения всех операций является логическое устройство. Обычно умножитель, сумматор и логическое устройство объединяются в один блок, называемый арифметико-логическим устройством (АЛУ). Связи между всеми блоками осуществляется с помощью шин, разрядность которых соответствует разрядности ячеек входной и выходной памяти.

Достоинством аппаратной реализации является высокое быстродействие.

С другой стороны, аппаратное решение ориентировано на узкоспециализированных задачах. Изменение алгоритма требует изменения структуры устройства, т.е. введения дополнительных функциональных блоков, что является недостатком.