 |
Главная |
Глава 2. Расчет температурного поля.
|
из
5.00
|
Математическая постановка задачи.
Расчет температурного поля ограждающих конструкций с математической точки зрения приводит к необходимости решения третьей краевой задачи для уравнения Лапласа. При этом нужно иметь в виду, что ограждающие конструкции, как правило, являются, неоднородными. Отсюда следует, что функция коэффициента теплопроводности является разрывной кусочно-постоянной функцией двух переменных.
Хотя алгоритм решение задачи остается верным для неоднородных ограждающих конструкций, мы, для примера, будем рассматривать однородную ограждающую конструкцию из дерева размером 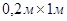 . Считаем, что по «краям» стенок, где проведен срез конструкции, установилась стабилизация температуры вдоль стенок, то есть отсутствует поток тепла на границах Г3 и Г4.
. Считаем, что по «краям» стенок, где проведен срез конструкции, установилась стабилизация температуры вдоль стенок, то есть отсутствует поток тепла на границах Г3 и Г4.
Наружная температура считается постоянной 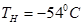 . Внутренняя температура в помещении считается постоянной
. Внутренняя температура в помещении считается постоянной 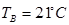 . Коэффициент теплоотдачи наружной поверхности ограждения
. Коэффициент теплоотдачи наружной поверхности ограждения 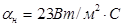 , коэффициент теплоотдачи внутренней поверхности ограждения
, коэффициент теплоотдачи внутренней поверхности ограждения 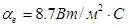 .
.
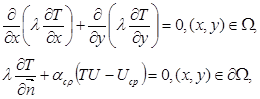 (3)
(3)
где 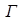 - граница области
- граница области 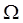 ;
;
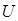 - искомая температура,
- искомая температура, 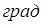 ;
;
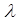 - коэффициент теплопроводности,
- коэффициент теплопроводности, 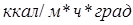 ;
;
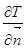 - производная по внешней нормали;
- производная по внешней нормали;
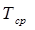 - температура среды (не зависит от времени),
- температура среды (не зависит от времени), 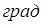 ;
;
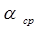 - коэффициент теплоотдачи поверхности ограждения,
- коэффициент теплоотдачи поверхности ограждения, 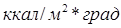 ;
;
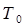 - начальная температура, град.
- начальная температура, град.
Решение будем искать методом Зейделя
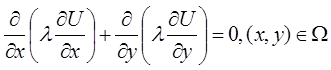 (1)
(1) 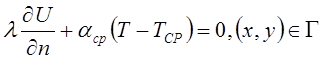 (3)
(3)
Граничные условия
Г1: 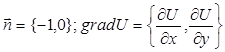
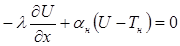
Г2: 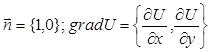
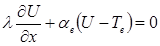
Г3: 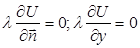
Г4: 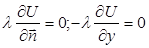
Метод Зейделя.
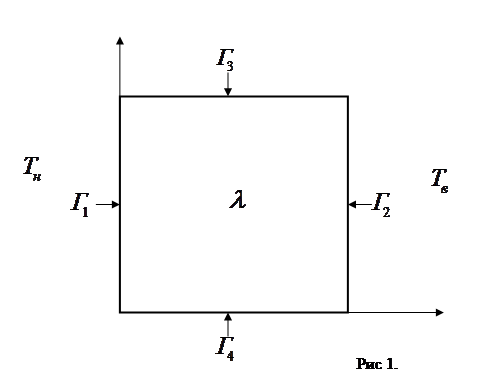
Прямоугольную декартову систему координат расположим, как показано на Рис.1.
Задачу (1) (3) будем решать конечно-разностным методом с помощью явной схемы.
Условие устойчивости явной схемы имеет вид
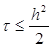
где 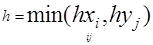 , если h=0.004, то
, если h=0.004, то 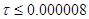
Расчет проводится до тех пор, пока температурное поле не выйдет на стационар, т.е. когда норма разности (равномерная норма) между соседними итерациями по времени не окажется меньше заданной погрешности 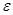 . В численных экспериментах полагали
. В численных экспериментах полагали 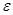 =0,0001.
=0,0001.
И вместо (1) (3) получим разностные уравнения
Этап
Начальное приближение 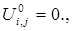
Этап
Для последующих итераций
2.1 (j=0)
Сперва находим значение в точке (0,0)
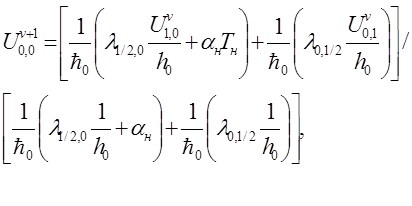
Затем находи значение в точках (i,0), i=1..n-1
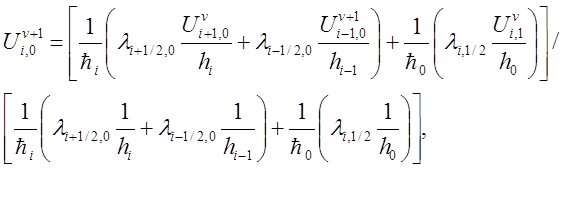
Затем находим значение в точке (n,0)
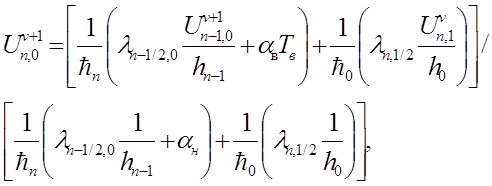
2.2 (j=1..n-1)
Сперва находим значение в точке (0,j)
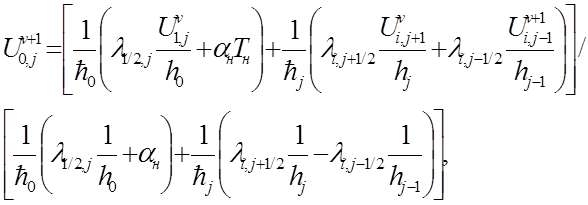
Затем находи значение в точках (i,j), i=1..n-1
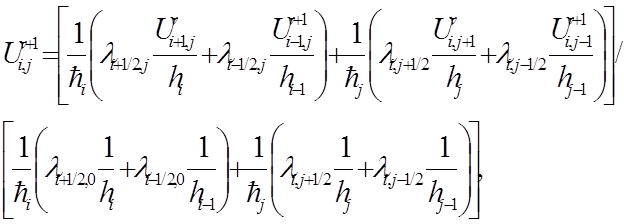
Затем находим значение в точке (n,j)
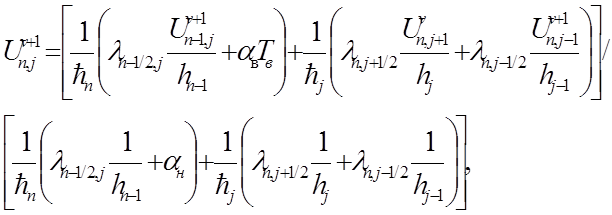
2.3 (j=n)
Сперва находим значение в точке (0,n)
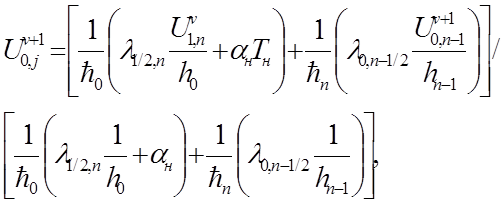
Затем находи значение в точках (i,n), i=1..n-1
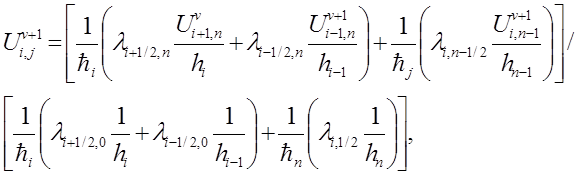
Затем находим значение в точке (n,n)
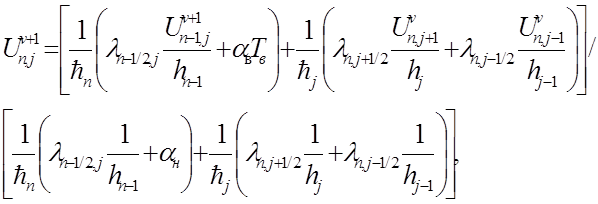
Этап
Вычисляем 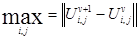 , пробегая по всем i,j.
, пробегая по всем i,j.
И проверяем 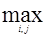 , если
, если 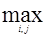 >= e, то переходим к этапу 2 до тех пор пока
>= e, то переходим к этапу 2 до тех пор пока 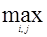 <e.
<e.
4 этап
Получили приближенное решение уравнения Лапласа методом Зейделя.
Метод Гаусса.
Для решения уравнения (1) (3) 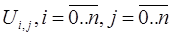 нужна матрица А размерности
нужна матрица А размерности 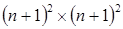 , ( n +1)2 неизвестных и ( n +1)2 уравнений. Ax=b, где
, ( n +1)2 неизвестных и ( n +1)2 уравнений. Ax=b, где 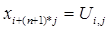
Но в нашем случае 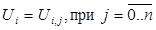 , и можем использовать матрицу размерности
, и можем использовать матрицу размерности 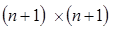 , ( n +1) неизвестных и ( n +1) уравнений.
, ( n +1) неизвестных и ( n +1) уравнений.
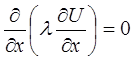
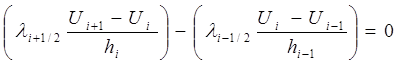
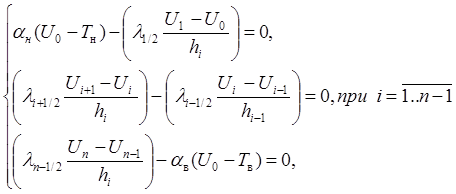
В нашем случае 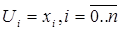
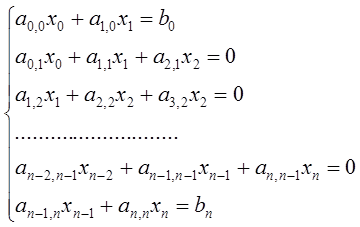
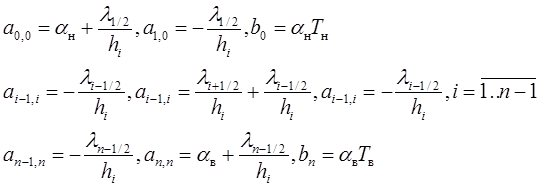
С помощью метода Гаусса находим решения системы.
Двухсеточный метод.
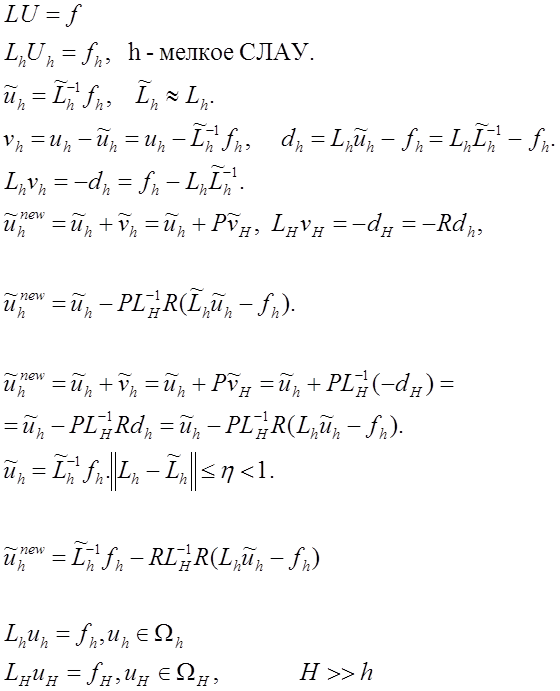
|
из
5.00
|
Обсуждение в статье: Глава 2. Расчет температурного поля. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

