 |
Главная |
Эквивалентные системы.
|
из
5.00
|
Рассмотрим класс систем
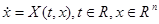
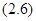
считая, что её правая часть непрерывно дифференцируемая. Будем говорить, что множество систем вида 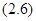 образует класс эквивалентности, если существует дифференцируемая функция
образует класс эквивалентности, если существует дифференцируемая функция 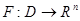 со свойствами:
со свойствами:
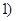 отражающая функция
отражающая функция  любой системы из рассматриваемого множества совпадает в области определения
любой системы из рассматриваемого множества совпадает в области определения  с функцией
с функцией 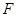 ;
;
 любая система вида
любая система вида 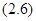 , отражающая функция
, отражающая функция  которой совпадает в области
которой совпадает в области  с функцией
с функцией 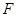 , содержится в рассматриваемом множестве.
, содержится в рассматриваемом множестве.
Две системы вида 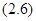 , принадлежащие одному классу эквивалентности, будем называть эквивалентными. Допуская определённую вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию
, принадлежащие одному классу эквивалентности, будем называть эквивалентными. Допуская определённую вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию  при этом будем называть отражающей функцией класса, а класс - соответствующим отражающей функции
при этом будем называть отражающей функцией класса, а класс - соответствующим отражающей функции  .
.
Для построения систем имеющих одну и ту же отражающую функцию можно воспользоваться теоремой:
Лемма 2.1 Для всякой непрерывно-дифференцируемой функции  , для которой выполнены тождества
, для которой выполнены тождества  , имеют место соотношения
, имеют место соотношения




Доказательство. Продифференцируем тождество  по
по 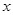 и по
и по  . Получим тождества
. Получим тождества
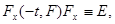

из которых следует неравенство  и тождества
и тождества  и
и  .
.
Лемма доказана.
Теорема 2.1. Пусть  есть отражающая функция некоторой дифференциальной системы с непрерывно дифференцируемой правой частью, а для дважды непрерывно дифференцируемой функции
есть отражающая функция некоторой дифференциальной системы с непрерывно дифференцируемой правой частью, а для дважды непрерывно дифференцируемой функции  выполнено
выполнено


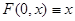

Тогда, для того, чтобы в области  функция
функция  совпадала с
совпадала с  , необходимо и достаточно, чтобы рассматриваемая система имела вид:
, необходимо и достаточно, чтобы рассматриваемая система имела вид:
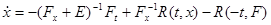
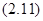
где 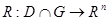 есть некоторая непрерывно дифференцируемая вектор-функция.
есть некоторая непрерывно дифференцируемая вектор-функция.
Доказательство. Необходимость. Пусть  есть отражающая функция некоторой системы
есть отражающая функция некоторой системы 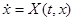 и пусть
и пусть  совпадает с
совпадает с  .
.
Положим

Тогда используя тождества  и
и  . и основное соотношение для отражающей функции
. и основное соотношение для отражающей функции  , получим тождества
, получим тождества





из которых следует, что всякая система, для которой  есть отражающая функция, может быть записана в виде
есть отражающая функция, может быть записана в виде 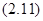 .
.
Достаточность. Пусть в системе 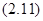
 есть такая функция, для которой решение системы
есть такая функция, для которой решение системы 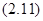 однозначно определяется своими начальными данными. Тогда, в чём можно убедиться подстановкой, выполняется основное соотношение для отражающей функции
однозначно определяется своими начальными данными. Тогда, в чём можно убедиться подстановкой, выполняется основное соотношение для отражающей функции  . Поэтому, согласно третьему свойству отражающей функции, функция
. Поэтому, согласно третьему свойству отражающей функции, функция  является отражающей функцией системы
является отражающей функцией системы  .
.
Теорема доказана.
Т.о. варьируя вектор-функцию  мы получим все системы имеющие заданную отражающую функцию.
мы получим все системы имеющие заданную отражающую функцию.
У эквивалентных систем одинаковое количество периодических решений, т.к начальные данные периодических решений определяются из уравнения  , где
, где  половина периода правой части соответствующих дифференциальных систем.
половина периода правой части соответствующих дифференциальных систем.
Пусть известно, что системы  и
и




принадлежат одному классу эквивалентности, и пусть одна из этих систем, скажем, система  является
является  периодической. Тогда если решения
периодической. Тогда если решения  и
и  систем
систем  и
и  соответственно продолжимы на отрезок
соответственно продолжимы на отрезок  , то
, то  , хотя система
, хотя система  может быть непериодической. Откуда следует
может быть непериодической. Откуда следует
Теорема 2.2. Пусть система  с
с  периодической по
периодической по  правой частью и система
правой частью и система  принадлежат одному классу эквивалентности, а их решения существуют при всех
принадлежат одному классу эквивалентности, а их решения существуют при всех  . Тогда между
. Тогда между  периодическими решениями системы
периодическими решениями системы  и решениями двухточечной задачи
и решениями двухточечной задачи  для системы
для системы  можно установить взаимооднозначное соответствие.
можно установить взаимооднозначное соответствие.
Уравнения

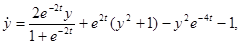
например, принадлежат одному классу эквивалентности с отражающей функцией  . Единственное
. Единственное  периодическое решение
периодическое решение 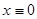
первого уравнения соответствует единственному решению задачи 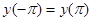 второго уравнения.
второго уравнения.
|
из
5.00
|
Обсуждение в статье: Эквивалентные системы. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

