Описание положения и движения МТ в системе отсчета.

Классическая механика. Лекция 1. Кинематика

 

1. Кинематика – это раздел механики, в котором изучаются способы математического описания движения тел. При этом причины движения не рассматриваются.

2. Система отсчета. Движение тела изучается в системе отсчета. Система отсчета состоит из трех обязательных компонентов: тела отсчета, относительно которого и происходит движение и инструментов для измерения движения тела: системы координат и часов.

3. Единица измерения. Для измерения положения точки изучаемого тела в системе отсчета используются единицы длины и времени:

3.1. Эталон длины, называемый метр.  Исторически за 1м принята длине парижского меридиана, деленная на 40 000 000.  Современное определение метра базируется на мировой константе – скорости света. Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды.

3.2. Для измерения времени между событиями, используется эталон времени – секунда. 1 секунда ранее определялась, как 1/86400 часть суток. Современное определение: Секунда — время, равное 9 192 631 770 периодам одного из видов излучения атома цезия-133.

4. Виды тел и движений, которые они совершают:

4.1. Самые сложные движения могут совершать деформируемые тела. Тело называется деформируемым, если расстояние между какими – либо его двумя точками могут изменяться во времени. Такие тела могут и совершать движения, как единое тело и его части могут двигаться друг относительно друга. Вообще говоря, все тела могут деформироваться, в той или иной степени.

4.2. Поэтому рассмотрим более простую модель тела– абсолютно твердое тело. Оно не может деформироваться. Простейшие формы движения такого тела – это поступательное и вращательное.

4.2.1. Поступательным называется движение, при котором все точки тела двигаются по одинаковым траекториям.

4.2.2. Вращательным называется движение тела, при котором у тела имеется ось вращения, т.е. прямая, все точки которой неподвижны. Все остальные точки тела движутся по окружностям, лежащим в плоскости перпендикулярной оси вращения и имеющим центр на этой оси. Сама ось неподвижна. Впрочем, возможно движение, когда ось вращения изменяет свое положение, но этот сложный вариант в школе не рассматривается.

4.2.3. Существует особый вид неравномерного движения – колебательное. Тело колеблется, если оно совершает движения, которые повторяются через некоторые промежутки времени. Если эти промежутки одинаковые, то такие колебания называются периодическими. Колебательное движение может состоять и из поступательных и из вращательных движений.

4.3. Материальная точка (сокращенно МТ), простейшая модель тела – это тело, размерами которого в данной модели или в задаче можно пренебречь. Также тело можно рассматривать, как МТ в случае поступательного движения абсолютно твердого тела, т.к. при этом движении все точки тела двигаются по одинаковым траекториям.

Описание положения и движения МТ в системе отсчета.

5.1. Положение МТ в системе отсчета определяется посредством системы координат, связанной с телом отсчета. Существуют различные системы координат. В данном курсе физики будет использоваться две: декартова и полярная. Вид и размещение системы координат выбираются произвольно, исходя из удобства в конкретной задаче. В частности, для изучения прямолинейного движения МТ, удобна декартова система координат.

В декартовой системе координат положение точки в пространстве определяется тремя числами – проекциями этой точки на оси координат.  Если движение МТ происходит в плоскости, то достаточно двух координат, а если по прямой, то достаточно и одной.

Полярная система координат на плоскости представляет собой одну ось координат (полярная ось) и радиус –вектор, начинающейся в точке начала отсчета (полюсе) и заканчивающийся в точке М, положение которой он определяет. Положение этой определяемой точки в полярной системе координат определяется длиной радиус-вектора r (радиальная координата) и углом его поворота относительно полярной оси ϕ (азимут): M(r,ϕ)   

5.2. 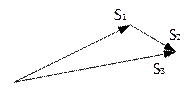Перемещение МТ - это направленный отрезок, соединяющий начальную и конечную точку движения МТ. Если МТ совершит последовательно два перемещения, то результатом будет направленный отрезок, которое получается если начало второго отрезка приложить к концу первого. Этот способ сложения перемещений показывает, что перемещение – это вектор, и сумма перемещений S₁ и S₂ это вектор S₃ = S₁ + S₂. Здесь буква, выделенная жирным шрифтом обозначает векторную величину (вместо стрелки над буквой).

Итак, перемещение – это вектор, соединяющий начальную и конечную точку движения. Модуль перемещения |S| измеряется в метрах. Модуль перемещения, как и модуль любого вектора, может быть вычислен по его проекциям S_x и S_y. По теореме Пифагора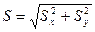

Пусть МТ перемещается из начальной точки M₀(x­₀, y₀) в произвольную точку M(x, y). Вектор перемещения S, зависящий от времени t, будет иметь проекции на оси координат: S_x=x – x₀ и S_y=y – y₀. Тогда движение МТ в плоскости описывается двумя уравнениями:

x = x₀ + S_x (t) и y = y₀ + S_y (t). Эти уравнения называются уравнениями движения МТ.  Как понятно, S_x (t) и  S_y (t) – функции времени.

5.3. Траектория движения – это линия, которую описывает при движении МТ, Пусть МТ за время Δt перемесилась из точки 1 в точку 2, совершив перемещение ΔS. Перемещение, совершенное МТ в единицу времени V_ср = ΔS/Δt называется средней скоростью. Скорость – это вектор, направленный так же, как перемещение. Единица измерения скорости 1 м/с. Если мы устремим время измерения к нулю Δt →0, то точка 2 устремиться к точке 1, вектор V станет касательной к траектории в точке 1, а его модуль |V_ср­|→ V. Полученный таким образом вектор V называется мгновенной скоростью МТ.

Мгновенная скорость – это вектор, показывающий направление перемещения, и его величину в единицу времени. Вектор скорости –функция времени. V =V(t). Скорость может изменяться, как по величине, так и по направлению.

5.4. Принцип независимости движения. Если точки участвует одновременно в нескольких перемещениях, то результирующее перемещение представляет собой векторную сумму этих перемещений: S(t) = S₁(t) + S₂(t) + S₃(t) …. Иначе говоря, перемещения не зависят друг от друга. Это так называемый принцип суперпозиции (наложения), который справедлив для многих явлений физики, например, для описания результата взаимодействий тела с несколькими другими телами.

В частности, функции S_x (t) и S_y (t) не зависят друг от друга. Т.е. может быть, что вдоль оси Y МТ вообще не двигается, т.е. S_y (t) = 0, или вдоль ось X тело движется равномерно, а вдоль Y – ускоренно.

Этот же принцип справедлив и для скорости тела, участвующего одновременно в нескольких движениях. Если равенство S(t) = S₁(t) + S₂(t) разделить на Δt, то получим: V(t) = V₁(t) + V₂(t). Это равенство позволяет вычислить скорость тела при переходе из одной системы отсчета в другую. Предположим, что МТ в некоторой системе отсчета X′Y′ имеет скорость V′. Назовем эту систему отсчета «собственной». Пусть собственная система отсчета сама движется в некоторой другой «лабораторной» системе отсчета, которую будем условно считать неподвижной, со скоростью V₀. Закон сложения скоростей определяет какая скорость будет у МТ в лабораторной системе отсчета: V= V′ + V₀. Это правило сложения скоростей, которое формулируется так: «Скорость тела в неподвижной системе отсчета равна векторной сумме его скорости в движущейся системе отсчета плюс скорость движущейся системы отсчета относительно неподвижной».

5.5. Ускорение.  Пусть вектор скорости V за время Δt изменится на величину ΔV.  ΔV – это тоже вектор. Причем вектор ΔV может быть направлен, как вдоль вектора V так и под любым углом к нему. Вектор a_ср = ΔV/Δt называется средним ускорением тела. Если Δt→0, то среднее ускорение стремиться к мгновенному ускорению a_ср→ a. Чтобы понять смысл вектора ускорения разложим его на две составляющие: одна a_τ – вдоль касательной к траектории, а значит и вдоль вектора V; другая – перпендикулярно касательной a_n. Вектор a_τ, называется тангенциальным ускорением. Он изменяет модуль вектора V на величину |a| в единицу времени. Вектор a_n называется нормальным или центростремительным ускорением. Он изменяет направление вектора V, не изменяя при этом его модуль. Единица измерения ускорения 1 м/с² или, как говорят один метр в секунду за секунду. 

5.6. Путь - это длина траектории движения. Она измеряется в метрах. Пусть за время Δt МТ прошла путь ΔL. Скорость при этом могла изменяться. Средней или путевой скоростью движения МТ называется путь, пройденный в единицу времени V_ср = ΔL/Δt. за все время движения Δt. Нужно заметить, что путь L всегда положителен. Так что, если тело двигалось вперед и назад вдоль траектории, то путь при этом только увеличивался. Путь равен модулю перемещения только когда тело двигается по прямой все время в одну сторону. Скорость при этом может меняться.

6. Описание движения тела во времени. В декартовой системе координат X,Y видна траектория тела и направление вектора его скорости. Однако величину вектора скорости вычислить нельзя, поскольку на ней отсутствует время. Чтобы вычислить скорость и ускорение тела нужно исследовать зависимости проекций его перемещения S_x (t) и S_y (t) от времени в системах координат (X,t) и (Y,t). Описание движения МТ в зависимости от времени сделаем на нескольких простых моделях движения:

6.1. Первая модель движения, которую мы рассмотрим, называется прямолинейное равномерное движение. Это движение, при котором траектория – прямая линия, а мгновенная скорость не изменяется, т.е. V=const. При прямолинейном движении достаточно одной координаты, чтобы определить положение МТ. Направим ось координат Х вдоль траектории перемещения. Пусть движение начинается с точки x₀. Тогда по определению скорости V= Δx/ Δt = (x –x₀) /Δt, где Δt = t - t₀. Перемещение S = x - x₀ = V Δt. Если отсчет времени вести от нуля, т.е.   t₀ =0, то Δt= t. Так можно получить уравнение: x(t)  = x₀ + Vt. Зависимость x(t) называется уравнением движения. В данном случае – это уравнение прямой линии. Нужно отметить два важных факта:

1. tg α угла наклона графика уравнения движения равен Δх/Δt = V скорости в данный момент времени. Для данного случая, где V= const он постоянен, но это утверждение верно и когда скорость меняется.

2. Площадь Δ F под графиком скорости в промежутке от t₁ до t₂ равна перемещению в этом интервале времени. V* (t₂ – t₁) = VΔt = ΔS. Это утверждение верно и для случая, когда скорость переменная.

6.2. Следующая модель движения – это равнопеременное прямолинейное движение МТ. Траектория движения – прямая линия, значит, положение МТ задается одной координатой Х. Равнопеременное – значит ускорение постоянно a(t) = const. Т.к.  движение прямолинейное, то ускорение направлено вдоль траектории – оси Х и его можно считать скаляром. Поскольку a = ΔV/Δt, то V-V₀ = a Δt и, считая, что t₀=0, получим уравнение для скорости V(t) = V ₀ + at. Поскольку а – скаляр то он может быть, как a>0, так и a<0. Соответственно, движение при этом будет или равноускоренным или равнозамедленным.

 Зависимость координаты МТ от времени найдем с помощью графика функции V(t).  Как было сказано выше площадь под этим графиком равна перемещению ΔF =Δх. Фигура под графиком – трапеция. Ее площадь F= Δx = Δt (V₂ + V₁)/ 2, где  Δt = t₂ –t_1. Будем считать , что  t₁ =0, а t₂ заменим на t.  Тогда: V₂ =V₁ +at, и x ( t ) = x ₀ + V ₀ t + at ² /2. Это уравнение равнопеременного движения.

6.2.1. Проанализируем его график. Понятно, что это парабола. Если a>0, то ветви параболы направлены вверх, а если a<0, то вниз. Координаты вершины параболы (t_m, x_m), найдем следующим образом. В вершине касательная горизонтальна, т.е. скорость в этой точке =0. Т.е. V = V₀ + at_m =0. Отсюда     t_m = - V₀ /a. Подставим это t_m в уравнение движения, считая для простоты, что x₀=0. Получим x_m = - V₀²/2a. Легко видеть, что уравнение параболы будет иметь вид: x = a/2(t+t_m) - x_m

6.2.2. Рассмотрим случай равнозамедленного движения a<0 на примере движения МТ под действием силы тяжести.  Сила тяжести для любого тела на поверхности Земли F_т = mg, где g =9,81 м/с²– вектор ускорения свободного падения, направленный вертикально вниз. Направим ось координат X вверх. Пусть тело имеет в точке х=0 начальную скорость V₀, направленную вверх.   Скорость V изменяется от V₀ при t=0 до нуля в точке максимального подъема  (t_m, x_m), а затем изменяет знак и начинает по модулю расти. Из симметрии параболы понятно, что в точке 2t_m тело падает на землю: x=0 и V= - V₀. Уравнение для скорости имеет вид (поскольку а = - g): V = V₀ –gt, уравнение движения x = V₀ t – gt²/2.  Время подъема t_m = V₀/g.  Максимальная высота подъема x_m = V₀²/2g

Следует обратить внимание на разницу между перемещением и путем. Модуль перемещения равен пути при прямолинейном однонаправленным движении. Как только направление движения меняется приращение перемещения меняет знак, а приращение пути остается положительным.

6.2.3. Получим формулу, связывающую начальную и конечную скорость равнопеременного движения с путем и ускорением. Для этого исключим время из системы уравнений: V_k= V_н +at и x = x₀ + V_нt + at²/2, где V_н -  начальная, а V_k – конечная скорость движения Для этого выразим t из первого уравнения t= (V – V₀) /a и подставим его во второе уравнение. Получим очень полезную для решения задач формулу V_к² – V_н² = 2a (x – x₀). Здесь х-х₀ – перемещение.

6.3. Движение МТ, брошенной под углом к горизонту. Описание движения тела, брошенного под углом к горизонту удобно выполнить, воспользовавшись принципом независимости движений. Будем считать, что МТ участвует одновременно в двух движениях: в равномерном движении по горизонтали вдоль оси Х и в равнозамедленном движении по вертикали вдоль оси Y.  

Пусть МТ брошена под углом α к горизонту с начальной скоростью V₀. Тогда начальная скорость движения вдоль оси Х равна V_0x = V₀ cos α = const, а начальная скорость движения вдоль оси Y равна V_0y = V₀ sin α. Поскольку движения независимы, то мы можем воспользоваться результатами, полученными при описании движения тела, брошенного вертикально вверх. В частности, время подъема до верхней точки траектории t_m = V_0y/g, высота подъема y_m = V_0y²/2g, время всего полета до точки падения t_к = 2t_m = 2V_0y/g. Дальность полета получим, умножив время полета на горизонтальную скорость L = 2V_0yV_0x/g.

 Найдем, как зависит дальность полета от угла бросания. L = 2 V₀sin α V₀cos α /g = V₀²/g * 2 sinα cosα = V₀²/g sin 2α. Заметим, что максимальная дальность получится при броске под углом π/4 = 45⁰, т.к. (sin α)_max = 1 при угле 2α = π/2 и равна она L_max = V₀²/g.  Чтобы построить график траектории движения y(x) запишем уравнение движения вдоль оси X: x = V_0x t и уравнение движения вдоль оси Y: y = V_0yt – gt²/2. Выразим время t из первого уравнения и подставим во второе.                   Получим: y = V_0y/V_{0x *} x – g/2V_0x² _* x², т.е траектория движения является параболой.

7. Равномерное движение МТ по окружности. Движение МТ по окружности удобно описывать в полярных координатах (R, ϕ). Для измерения угла ϕ используется радианная мера угла – отношение дуги, на которую опирается угол к радиусу:        ϕ =  _͝͝  AB/R. Полный угол в радианах ϕ_пол= 2π R/R = 2π. Поскольку в градусах полный угол = 360⁰, то 1 рад = 360/2π = 57,3⁰.

Скорость точки V=ΔS/Δt. Поскольку путь – это длина дуги, то  ΔS =Δϕ R и  V= Δϕ/Δt _*R. Обозначим скорость изменения угловой координаты в единицу времени ω = Δϕ/Δt. Она называется угловая скорость. Линейная скорость связана с угловой скоростью соотношением V = ω R. Размерность [ω]= 1/сек. Кроме того, равномерное движение по окружности может быть описано периодом, т.е.  временем одного оборота T = 2π/ω и частотой ν = 1/T  - числом оборотов в секунду. Частота измеряется в Гц (1/сек).

При движении по окружности вектор скорости V изменяет свое направление, следовательно – это движение с ускорением. Поскольку модуль вектора не меняется, то это нормальное ускорение, которое перпендикулярно вектору скорости и направлено оно к центру окружности. Оно называется центростремительным. Ускорение по определению  а_цс = ΔV /Δt. На рисунке видно, как тело, перемещаясь на  угол Δϕ изменяет свою скорость с V на V ₁ , за счет прибавления Δ V . Из треугольника скоростей видно, что дуга VV₁ = V Δϕ (из определения радианной меры угла). Но дуга VV₁ при малых Δϕ стремится к хорде ΔV. Таким образом, ΔV= V Δϕ. Разделим это уравнение на  Δt . Получим ΔV/ Δt = V Δϕ/Δt = V ω = V²/R. Следовательно, центростремительное ускорение a_цс = V²/R = ω²R.

8. Формулы и константы.

8.1. Равномерное прямолинейное движение                                                       Уравнения движения: V=const; x = x₀ +Vt;

8.2. Равнопеременное прямолинейное движение                                                           Уравнения движения: а = const; V(t) = V₀ +at; x = x₀ + V₀t + at²/2                           Уравнение в форме выделенного полного квадрата: х= a/2 (t + V₀/a)² – V₀²/2a                Соотношение между скоростями: V_к² – V_н² = 2a (x – x₀)

8.3. Движение по вертикали в однородном поле сил тяжести                                       Уравнения движения: V=V₀ – gt; x = x₀ + V₀t – gt²/2                                                Уравнение в форме выделенного полного квадрата x = -g/2(t – t_m)² ₊ x_m,                          где t_m= V₀/g – время подъема тела на максимальную высоту,                                x_m=V₀²/2g – максимальная высота.

8.4. Движение тела, брошенного под углом к горизонту                                                             Время подъема до верхней точки траектории t_m = V_0y/g,                                          Высота подъема h_m = V_0y²/2g,                                                                                       Время всего полета до точки падения t_к = 2t_m = 2V_0y/g.                                                Дальность полета L = 2V_0yV_0x/g                                                                         

8.5. Равномерное движение по окружности    

Угловая скорость ω = Δφ/Δt = 2πν

Связь линейной и угловой скорости V=ωR

Период вращения T = 2π/ω

Частота вращения ν = 1/T = ω / 2π

Центростремительное ускорение а_цс =V²/R = ω²R