Практическая реализация

Оглавление

Введение

1. Теоретическая часть

2. Практическая реализация

2.1 Проектирование интерфейса

2.2 Программирование вычисления

2.3 Визуализация метода

2.4 Вычислительный эксперимент

Заключение

Перечень используемой литературы

Введение

Данный проект разработан для вычисления коней нелинейного уравнения методом итераций. Программа написана на языке высокого уровня Delphi.

Пояснительная записка состоит из следующих разделов:

1 Теоретическая часть – теория, описывающая правила вычисления коней нелинейного уравнения методом итераций, а также блок-схема метода.

2 Практическая реализация:

2.1 Проектирование интерфейса – создание и описание элементов (частей) из которых состоит данная программа.

2.2 Программирование вычисления – конечный результата работы.

2.3 Визуализация метода – последовательный показ работы проекта на вычисление корней уравнения методом итераций

2.4 Вычислительный эксперимент – сравнение результатов программы с решением в математическом пакете Mathcad 14.

3 Заключение о проделанной работе.

Теоретическая часть

Часто приходится находить корни уравнений вида 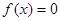, где f(x) определена и непрерывна на некотором интервале.

Если f(x) представляет собой многочлен, то уравнение 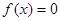 - алгебраическое, если в функцию входят функции типа: тригонометрических, логарифмических, показательных и т.п., то уравнение называется трансцендентным.

Решение уравнения вида 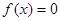 разбивается на два этапа:

1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2. вычисление выделенного корня с заданной точностью.

Первый этап более сложный, в этом случае может помочь построение приближенного графика функции с анализом на монотонность, смену знака, выпуклость и т.д.

Для вычисления выделенного корня существует множество методов, например:

- метод итераций;

- метод половинного деления;

- метод Ньютона.

На рисунке 1 представлен график функции y=x-2+sin(1/x)

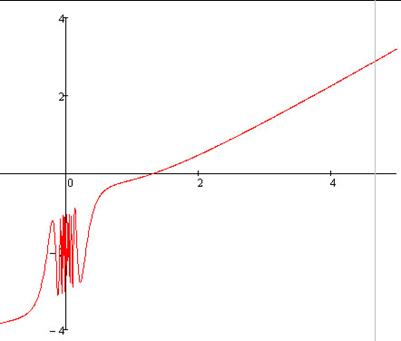
Рис. 1

В данной курсовой работе будет рассмотрено нахождение корней уравнения x-2+sin(1/x)=0 методом итераций.

Уравнение 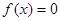 можно представить в виде: 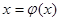. То есть

x-2+sin(1/x)=0→ x=2-sin(1/x)

Далее на отрезке [a,b], где функция имеет корень, выбирается произвольная точка x₀ и далее последовательно вычисляется:

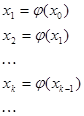
Процесс вычисления значений x_k называется итерационным процессом.

Если на отрезке [a,b] выполнено условие |φ΄(x)| ≤ q <1, то итерационный процесс сходится к корню уравнения .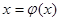

Если необходимо вычислить корень с точностью ε, то процесс итераций продолжается до тех пор, пока для двух последовательных приближений x_n и x_n-1 не будет выполнено:

,

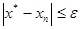где ε задается погрешностью корня x*.

Соответственно описанной выше методике составим блок–схему решения уравнения методом итераций[2].

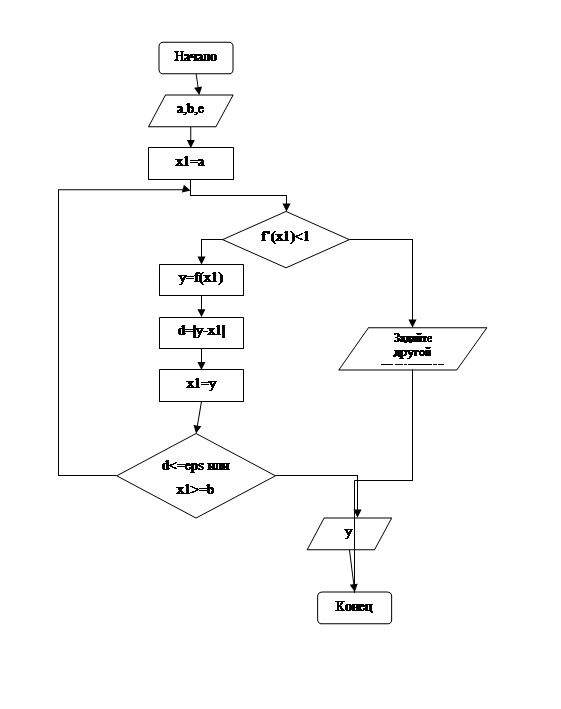
Практическая реализация