 |
Главная |
Уравнения динамики для вероятностных состояний (уравнения Колмогорова). Предельные вероятности состояний.
|
из
5.00
|
Формально дифференцируя уравнение Колмогорова—Чепмена по s при s = 0 получаем прямое уравнение Колмогорова:

где

Формально дифференцируя уравнение Колмогорова — Чепмена по t при t = 0 получаем обратное уравнение Колмогорова

Необходимо подчеркнуть, что для бесконечномерных пространств оператор  уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.
уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.
В том случае, если число состояний системы S является конечным и из каждого состояния представляется возможным перейти (за то или иное количество шагов) в каждое другое состояние, то предельные вероятности состояний существуют, а также не зависят от начального состояния системы.
На рис. показаны граф состояния и переходов, удовлетворяющие поставленному условию: из любого состояния система рано или поздно может перейти в любое другое состояние. Условие не будет выполняться при изменении направления стрелки 4—3 на графе рис , а на противоположное.
Допустим, что поставленное условие выполнено, и, следовательно, предельные вероятности существуют:

Предельные вероятности будут обозначаться теми же буквами  что и вероятности состояний, при этом под ними подразумеваются числа, а не переменные величины (функции времени).
что и вероятности состояний, при этом под ними подразумеваются числа, а не переменные величины (функции времени).

Ясно, что предельные вероятности состояний должны давать в сумме единицу:  Следовательно, в системе
Следовательно, в системе  при
при  устанавливается некоторый предельный стационарный режим: пусть система и меняет собственные состояния случайным образом, однако вероятность каждого из этих состояний не зависит от времени и каждое из них осуществляется с некоторой постоянной вероятностью, представляющей собой среднее относительное время пребывания системы в этом состоянии.
устанавливается некоторый предельный стационарный режим: пусть система и меняет собственные состояния случайным образом, однако вероятность каждого из этих состояний не зависит от времени и каждое из них осуществляется с некоторой постоянной вероятностью, представляющей собой среднее относительное время пребывания системы в этом состоянии.
15. Процесс гибели и размножения.

Марковским процессом гибели и размножения с непрерывным временем назовем такой с.п., который может принимать только целые неотрицательные значения; изменения этого процесса могут происходить в любой момент времени t, при этом в любой момент времени он может либо увеличиваться на единицу, либо остаться неизменным.
Потоками размножения λi(t) будем называть пуассоновские потоки, ведущие к увеличению функции X(t). Соответственно μi(t) – потоки гибели, ведущие к уменьшению функции X(t).
Составим по графу уравнения Колмогорова:

Если поток с конечным числом состояний:

Система уравнений Колмогорова для процесса гибели и размножения с ограниченным числом состояний имеет вид:

Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю.

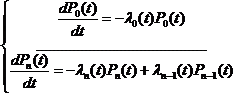
Процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

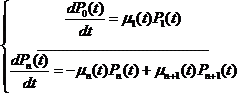
16. Системы массового обслуживания с отказами.
Наиболее простой из рассматриваемых задач в рамках теории массового обслуживания является модель одноканальной СМО с отказами или потерями.
Следует отметить, что в данном случае количество каналов равно 1  (). Этот канал принимает пуассоновский поток заявок, интенсивность которого равняется
(). Этот канал принимает пуассоновский поток заявок, интенсивность которого равняется  . Время оказывает влияние на интенсивность:
. Время оказывает влияние на интенсивность:

Если заявка прибыла в канал, который в данный момент не является свободным, она получает отказ и больше не числится в системе. Обслуживание заявок осуществляется в течение случайного времени  , распределение которого реализуется в соответствии с показательным законом с параметром
, распределение которого реализуется в соответствии с показательным законом с параметром  :
:


17. Системы массового обслуживания с ожиданием.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если заявка пришла в момент, когда в очереди уже стоят m заявок, она покидает систему необслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
 —канал свободен;
—канал свободен;
 —канал занят, очереди нет;
—канал занят, очереди нет;
 — канал занят, одна заявка стоит в очереди;
— канал занят, одна заявка стоит в очереди;
 —канал занят, k - 1 заявок стоят в очереди;
—канал занят, k - 1 заявок стоят в очереди;
 — канал занят, т заявок стоят в очереди.
— канал занят, т заявок стоят в очереди.

|
из
5.00
|
Обсуждение в статье: Уравнения динамики для вероятностных состояний (уравнения Колмогорова). Предельные вероятности состояний. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

