Алгоритм расчёта параметров на режиме

Сложность и нелинейность полученной модели котла-утилизатора не позволяют решать систему уравнений для ПГУ аналитически. Решение с необходимой точностью может быть получено методом последовательных приближений. Задавшись некоторыми начальными значениями ряда параметров, производят расчёт системы по имеющимся формулам и получают уточнённые значения тех же параметров, которые, если они расходятся с принятыми ранее более чем на заданную величину, подставляются в следующую итерацию. Для проведения численного расчёта на сходимость используется алгоритм со вложенными циклами, реализованный на базе электронных таблиц OpenOffice.org Calc с программированием циклов и подстановок на встроенном BASIC.

Форма представления расчётных зависимостей оказывает существенное влияние на скорость и устойчивость сходимости. Например, уравнение Стодолы можно применить для определения начального давления процесса расширения, но следует избегать его применения для расчёта конечного давления, поскольку полученная величина имеет сравнительно большой разброс и процесс вычисления может завершиться ошибкой извлечения корня из отрицательного числа. Также уравнение теплоотдачи

при решении совместно с уравнениями теплового баланса

,    
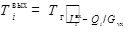сходится по конечным темпера­турам сред и тепловому потоку достаточно плохо, а может и расходиться (система неустойчива по отклонению температур). Значительно лучше сходится система, где уравнение теплопередачи заменено на эквивалентную подсистему

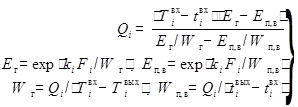.<лучше вычитать наоборот>

Данное выражение может быть заложено в отдельную подпрограмму, которая после небольшого числа циклов производит расчёт теплообменника по входным температурам и расходам сред, давлениям пара на входе и выходе, составу уходящих газов и комплексу k_iF_i. Пример такой подпрограммы приведён в приложении 5. Теплофизические свойства веществ в программе определяются по полиномам из [2] (для газов) и формуляции IF‑97 (для воды и пара). Аналогичные выражения для испарительного элемента с известной входной темпера­турой газов и элемента с одной фазой, у которого заданы темпера­туры сред на горячем конце, принимают вид соответственно

, .

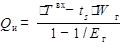Расход греющего пара на деаэратор по отношению к расходу конденсата можно определить как

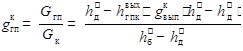
(следствие из теплового баланса деаэра­тора: теплота насыщенного пара из барабана тратится на догрев конденсата до темпера­туры насыщения в деаэра­торе и испарение выпара, вследствие чего греющий пар конденсируется). Расход конденсата, в свою очередь, должен быть таким, чтобы питать расход пара и продувки и выпар:

,
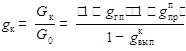где – один из параметров сходимости. Зная расход греющего пара, легко найти все расходы по элементам КУ из их материальных балансов.

Кроме того, для улучшения сходимости можно использовать переходы, отличающиеся от простой подстановки нового значения (при этом последовательность таких переходов должна сходиться к требуемой величине). Например, итерации по недогреву в экономайзере 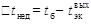 выполняют переход в зависимости не только от значения, определённого по расчёту элементов, но и от значений, принятого изначально и полученного на предыдущей итерации (см. алгоритм). Циклы с мало зависящими друг от друга переменными для упрощения алгоритма можно объединять; в самом внешнем (нулевого уровня) цикле все критерии сходимости опять проверяются, и если хотя бы один из них не выполнен, расчёт продолжается (циклы остальных уровней реализованы с постусловием).

Список переменных, определяемых для данного алгоритма методом последовательных приближений, представлен в таблице 4; сам алгоритм приведён в приложении 2. После 51 цикла нижнего уровня (по t₀) алгоритм сошёлся с требуемой точностью, результаты приведены в таблице 5.

Таблица 3. Организация расчёта на сходимость: циклы и переменные

Уровень цикла	Наименование величины	Обозна­чение	ЕИ	Критерий сходимости	Новое значение	Число шагов
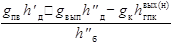
1	Удельный расход греющего пара	gгп	–			17
	Недогрев в эконо­май­зере до tб	δtнед	град.
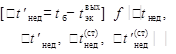
	Температура в конденсаторе	tк	град.
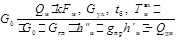
2	Расход свежего пара	G0	кг/с			48
3	Температура свежего пара	t0	град.		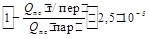	51