ИСПОЛЬЗОВАНИЕ СЕТЕЙ ПЕТРИ ПРИ ПЕРЕХОДЕ ОТ ГРАММАТИКИ К МИНИМАЛЬНОМУ АВТОМАТУ

Построим для грамматики G' сеть Петри. Это можно сделать, поставив в соответствие нетерминальным символам позиции (кружки) сети, а терминалам – переходы (планки) сети. Будем помечать позиции и переходы соответствующими нетерминалами и терминалами. Поскольку сеть Петри является двудольным графом, соединение дугами позиций разрешается только через переходы, а переходов - через позиции. Если в правой части некоторого правила вывода из R' имеет место конкатенация терминалов, то в сети Петри между переходами, помеченными терминалами, должны появляться дополнительные позиции, которые можно помечать символами левой части правила вывода с верхними индексами 1, 2, ... . Так, фрагмент сети Петри, соответствующий первому правилу вывода (S ® x5 x6 x0 A) , будет иметь вид, показанный на рис. 4. При построении остальных фрагментов, соответствующих последующим правилам вывода, следует использовать ранее обозначенные позиции (но не переходы!). Таким образом, позиции могут иметь несколько входящих и исходящих дуг, но переходы – в точности по одной входящей и не более чем одной исходящей дуге (исходящая дуга может отсутствовать, если в правой части правила вывода отсутствует замыкающий нетерминал).

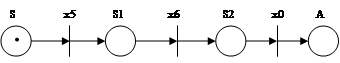
Рис. 4. Фрагмент интерпретированной сети Петри, соответствующий правилу вывода S ® x5 x6 x0 A

Маркером отмечается позиция, соответствующая начальному символу грамматики G' (в данном случае это позиция S).

В остальном правила построения сети Петри ясны из рассматриваемого сквозного примера - сравнить правила R' с рис. 5.

Рис. 5. Сеть Петри, соответствующая исходной грамматике

Понятно, что сеть на рис. 5 представляет собой ни что иное, как автоматную сеть Петри (подкласс сетей Петри) и что позиции можно трактовать как состояния конечного автомата, а переходы - как входные символы.

Для полноты соответствия построенной сети Петри распознающему автомату Мура введем не показанную на рис. 5 заключительную позицию Z, в которую направим дуги из всех переходов, ранее не имевших исходящих дуг (см. рис. 6).

Рис 6. Сеть Петри, дополненная заключительной позицией Z .

Теперь следует заметить, что в сети на рис. 6 имеются три идентичных фрагмента, содержащие позиции A, B и C, каждой из которых инцидентны по два выходных перехода x2 и x5, и еще два идентичных фрагмента с позициями D и E, каждой из которых инцидентен выходной переход x3.

Функционирование сети не изменится, если склеить идентичные фрагменты. Позиции S1 и S3; F1 и F4; F2 и F5; F3, F6 и F8 также можно склеить (см. рис. 7).

Рис. 7. Преобразованная недетерминированная сеть Петри

Этот этап соответствует минимизации числа состояний автомата, но он выполнен для автомата, сохраняющего недетерминированность. Источником недетерминированности, очевидно, могут являться лишь позиции свободного выбора, исходящие дуги которых являются входящими дугами переходов, помеченных одинаковыми терминалами. В данном случае к таким позициям следует отнести лишь позицию (S1, S3). Способ устранения недетерминированности виден из рисунка 9.

Рис. 8 . Типичный пример устранения недетерминированности

Недетерминированность устраняется склеиванием двух позиций P_l и P_k в одну (P_l, P_k). При этом позиции (P_l, P_k) инцидентны все исходящие дуги, ведущие в переходы tr, tq, ts, являющиеся исходящими дугами позиций P_l и P_k.

Применим этот способ к сети на рис. 7, получим сеть, показанную на рисунке 9.

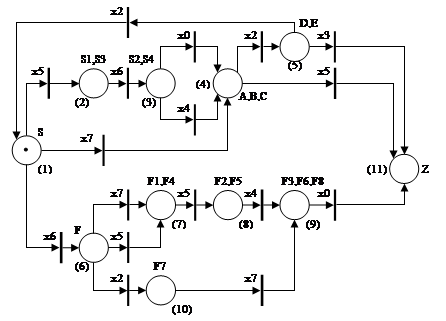
Рис. 9. Минимизированная детерминированная сеть Петри

В данном случае можно установить взаимно однозначное соответствие между сетью рис. 9 и графом переходов минимального автомата – рис. 3. (В скобках на рис. 9 указаны соответствующие состояния минимального автомата).

Указание. Выполнение обоих способов построения минимальнного автомата обязательно, так как это обеспечивает контроль правильности выполнения этапов курсовой работы.

От рис. 9 можно перейти к графу переходов автомата, заменив переходы сети Петри дугами автомата, переименовав позиции сети соответствующими им состояниями автомата и взвесив дуги наименованиями этих переходов.