Результат работы программы

Результат работы программы рисования куба с нормалями приведен на Рис. 7.

 

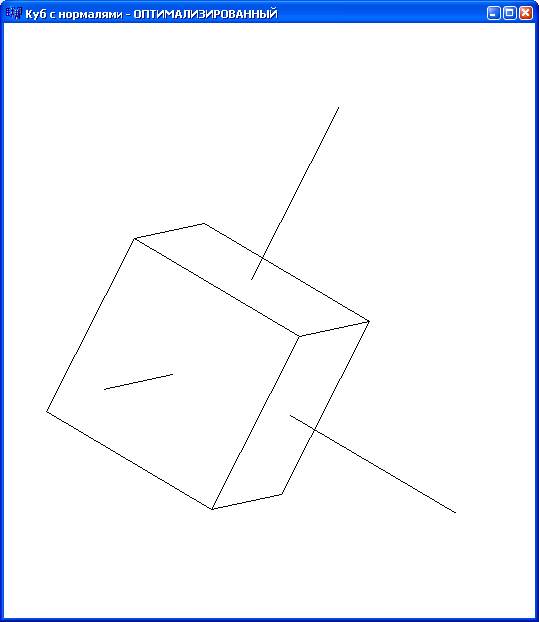
Рис. 7

 

OpenGL

Поверхность

Введение

 

Поверхность задана формулой:

 

Z (x, y) = (sin x² + cos y² ) xy

 

Решение

 

Функцию будем искать учитывая:

 

x  [– 0,8; 0,8]

y  [– 1,5; 1,5]

 

Шаг итерации равен 0,03.

Для правильного отображения освещения необходимо найти нормали в каждой точке поверхности.

 

F (x, y, z) = 0, z = f(x, y), т.е. F = f(x, y) – z = 0,

 

Следовательно, нормали вычислим так:

Найдем частные производные:

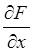 = 2 x x y cos x²+(sin x² + cos y²) y

 = – 2 x y y sin y²+x (sin x² + cos y²)

 

Текст программы

 

double Z(double x,double y)

{

double z=(sin(x*x)+cos(y*y))*x*y;

return z;

}

double dZx(double x,double y)

{

double pr=2*x*x*y*cos(x*x)+(sin(x*x)+cos(y*y))*y;

return pr;

}

//-------------------------------------------------------------------

double dZy(double x,double y)

{

double pr=(-2)*x*y*y*sin(y*y)+x*(sin(x*x)+cos(y*y));

return pr;

}

 

//-------------------------------------------------------------------

void Draw()

{

Vector Norm;

glPolygonMode(GL_FRONT_AND_BACK,GL_FILL);

for(double x=-0.8; x<0.8; x=x+0.03)

{

for(double y=-1.5; y<1.5; y=y+0.03)

{

glBegin (GL_QUADS);

 

    glTexCoord2d(0, 0);

Norm=Vector(dZx(x,y),dZy(x,y),-1);

glNormal3d(Norm.x,Norm.y,Norm.z);

glVertex3d(x,y,Z(x,y));

 

glTexCoord2d(0, 1);

Norm=Vector(dZx(x+1,y),dZy(x+1,y),-1);

glNormal3d(Norm.x,Norm.y,Norm.z);

glVertex3d(x+1,y,Z(x+1,y));

 

glTexCoord2d(1,1);

Norm=Vector(dZx(x+1,y+1),dZy(x+1,y+1),-1);

glNormal3d(Norm.x,Norm.y,Norm.z);

glVertex3d(x+1,y+1,Z(x+1,y+1));

 

glTexCoord2d(1,0);

Norm=Vector(dZx(x,y+1),dZy(x,y+1),-1);

glNormal3d(Norm.x,Norm.y,Norm.z);

glVertex3d(x,y+1,Z(x,y+1));

glEnd();

}

}

}

 

//----------------------- Рисование сцены --------------------------

void __fastcall TFormMain::DrawObjects()

{

glBindTexture(GL_TEXTURE_2D,texture1);

Draw();

 

}

 

 

Результат работы программы

Результат работы программы рисования поверхности приведен на Рис. 8.

 

Рис. 8

 

Пружина

Введение

 

Пружина – модификация тора, получаемая из последнего путем распространения вдоль оси OZ, при этом большой радиус не меняется.

 

Формула пружины:

 

x = (R + r cos(f)) sin(k w),

y = (R + r cos(f)) cos(k w),

z = r sin(f) + k w,

 

где k – константа, определяющая шаг витков спирали по высоте. Углы f и w должны изменяться в полном круговом диапазоне, например от 0 до 360.

 

Решение

 

Поверхность пружины полностью определена формулами (см. пункт «2.2.2.1. Введение»).

 

Для правильного отображения освещения необходимо найти нормали в каждой точке поверхности пружины. Нормали вычислим, используя класс VECTOR, где нормали определяются в соответствии правилу:

 

1. Берем два вектора лежащих в одной плоскости полигона и исходящих из одной точк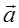и  и .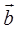

 

Координаты этих векторов определяются так:

V1 (x1, y1, z1), V2(x2, y2, z2) – две вершины, тогда вектор, проходящий через эти точки равен

= (x2-x1, y2-y1, z2-z1)

 

2. Вычисляем , векторное произведение векторов  и

 

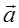 =  x 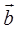 = ( (a_y b_z – a_z b_y), (a_x b_z – a_z b_x), (a_x b_y – a_y b_x) )

 

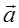 ┴  и  ┴ 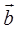, значит  – нормаль к полигону.

Затем на поверхность пружины накладываем текстуру, которую берем из bmp-файла.

 

Текст программы

 

void DrawPruzina(double R,double r,double x,double y,double z)

{

 const int N=50; // число хорд в окружности

 const int M=200; // число окружностей в пружине

 const int k=2; // константа, определяющая число витков пружины

 

 Vector V[N][M];

 Vector Norm[N][M];

 Vector NormV[N][M];

 glTranslatef(x,y,z);

 glPolygonMode(GL_FRONT_AND_BACK,GL_LINE);

 

 //вычисление вершин

 

 for(int i=0;i<N;i++)

 {

for(int j=0;j<M;j++)

{

V[i][j].x=(R+r*cos(i*2*3.14/N))*sin(j*k*2*3.14/M);

V[i][j].y=(R+r*cos(i*2*3.14/N))*cos(j*k*2*3.14/M);

V[i][j].z=r*sin(i*2*3.14/N)+k*j*3.14/M;

}

 }

 

//вычисление нормалей к полигонам

 for(int i=0;i<N-1;i++)

 {

for(int j=0;j<M-1;j++)

{

Norm[i][j]=(V[i+1][j]-V[i][j])^(V[i][j+1]-V[i][j]);

Normalize( Norm[i][j]);

}

 }

 for(int i=0;i<N-1;i++)

 {

Norm[i][M-1]=(V[i+1][M-1]-V[i][M-1])^(V[i][0]-V[i][M-1]);

Normalize(Norm[i][M-1]);

 }

 for(int j=0;j<M-1;j++)

 {

Norm[N-1][j]=(V[0][j]-V[N-1][j])^(V[N-1][j+1]-V[N-1][j]);

Normalize(Norm[N-1][j]);

 }

 Norm[N-1][M-1]=(V[0][M-1]-V[N-1][M-1])^(V[N-1][0]-V[N-1][M-1]);

 Normalize( Norm[N-1][M-1]);

 

//вычисление нормалей к вершинам

for(int i=1;i<N;i++)

 {

for(int j=1;j<M;j++)

{

NormV[i][j]=(Norm[i][j]+Norm[i-1][j]+Norm[i][j-1]+Norm[i-1][j-1])/4;

Normalize(NormV[i][j]);

}

 }

 for(int i=1;i<N;i++)

 {

NormV[i][0]=(Norm[i][0]+Norm[i-1][0]+Norm[i][M-1]+Norm[i-1][M-1])/4;

Normalize(NormV[i][0]);

 }

 for(int j=1;j<M;j++)

 {

NormV[0][j]=(Norm[0][j]+Norm[N-1][j]+Norm[0][j-1]+Norm[N-1][j-1])/4;

Normalize(NormV[0][j]);

 }

NormV[0][0]=(Norm[0][0]+Norm[N-1][0]+Norm[0][M-1]+Norm[N-1][M-1])/4;

Normalize(NormV[0][0]);

 

// рисуем пружину

glBegin(GL_QUADS);

 for(int i=0;i<N-1;i++)

 {

for(int j=0;j<M-1;j++)

{

glNormal3d(NormV[i][j].x,NormV[i][j].y,NormV[i][j].z);

glTexCoord2d((double)i/N,(double)j/M);

glVertex3d(V[i][j].x,V[i][j].y,V[i][j].z);

 

glNormal3d(NormV[i+1][j].x,NormV[i+1][j].y,NormV[i+1][j].z);

glTexCoord2d((double)(i+1)/N,(double)j/M);

glVertex3d(V[i+1][j].x,V[i+1][j].y,V[i+1][j].z);

 

glNormal3d(NormV[i+1][j+1].x,NormV[i+1][j+1].y,NormV[i+1][j+1].z);

glTexCoord2d((double)(i+1)/N,(double)(j+1)/M);

glVertex3d(V[i+1][j+1].x,V[i+1][j+1].y,V[i+1][j+1].z);

 

glNormal3d(NormV[i][j+1].x,NormV[i][j+1].y,NormV[i][j+1].z);

glTexCoord2d((double)i/N,(double)(j+1)/M);

glVertex3d(V[i][j+1].x,V[i][j+1].y,V[i][j+1].z);

}

 }

 

 glEnd();

 

}

//-------------------------- Рисование сцены ------------------------------

void __fastcall TFormMain::DrawObjects()

{

 

 glBindTexture(GL_TEXTURE_2D,texture1);

 DrawPruzina(3,1,0,0,0);

}

 

//------------------- Загружаем текстуру из файла -------------------------

void __fastcall TFormMain::SetupTextures()

{

 bitmap = new Graphics::TBitmap;

bitmap->LoadFromFile("pic.bmp");

GLubyte bits1[64][64][4];

GLubyte bits2[64][64][4];

GLubyte bits3[64][64][4];

for(int i = 0; i < 64; i++)

{

for(int j = 0; j < 64; j++)

   {

       bits1[i][j][0]= (GLbyte)GetRValue(bitmap->Canvas->Pixels[i][j]);

       bits1[i][j][1]= (GLbyte)GetGValue(bitmap->Canvas->Pixels[i][j]);

       bits1[i][j][2]= (GLbyte)GetBValue(bitmap->Canvas->Pixels[i][j]);

       bits1[i][j][3]= (GLbyte)255;

   }

}

glPixelStorei(GL_UNPACK_ALIGNMENT, 4);

  glGenTextures(1, &texture1);

glBindTexture(GL_TEXTURE_2D, texture1);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);

glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 64, 64, 0, GL_RGBA, GL_UNSIGNED_BYTE, bits1);

glEnable(GL_TEXTURE_2D);

glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);

}

 

//------------------------- Параметры освещения ---------------------------

 

void __fastcall TFormMain::SetupLighting()

{

GLfloat MaterialAmbient[] = {1.0, 1.0, 1.0, 1.0};

GLfloat MaterialDiffuse[] = {1.0, 1.0, 1.0, 1.0};

GLfloat MaterialSpecular[] = {1.0, 1.0, 1.0, 1.0};

GLfloat MaterialShininess[] = {100.0};

GLfloat AmbientLightPosition[] = {0.5, 1.0, 1.0, 0.0};

GLfloat LightAmbient[] = {0.5, 0.5, 0.5, 1.0};

 

glMaterialfv(GL_FRONT, GL_AMBIENT, MaterialAmbient);

glMaterialfv(GL_FRONT, GL_DIFFUSE, MaterialDiffuse);

glMaterialfv(GL_FRONT, GL_SPECULAR, MaterialSpecular);

glMaterialfv(GL_FRONT, GL_SHININESS, MaterialShininess);

glLightfv(GL_LIGHT0, GL_POSITION, AmbientLightPosition);

glLightModelfv(GL_LIGHT_MODEL_AMBIENT, LightAmbient);

 

glEnable(GL_LIGHTING);

glEnable(GL_LIGHT0);

glEnable(GL_COLOR_MATERIAL);

glColorMaterial(GL_FRONT, GL_AMBIENT_AND_DIFFUSE);

glShadeModel(GL_SMOOTH);

}