Глава III . Связь законов сохранения с пространством и временем.

2019-12-29

194

Обсуждений (0)

0.00 из 5.00 0 оценок

§ 1. Теорема Э. Нётер.

Теорема Эмми Нётер[1] утверждает, что каждой симметрии физической системы соответствует некоторый закон сохранения. Так, закон сохранения энергии соответствует однородности времени, закон сохранения импульса — однородности пространства, закон сохранения момента импульса — изотропии пространства, закон сохранения электрического заряда — калибровочной симметрии и т. д.

Теорема обычно формулируется для систем, обладающих функционалом[2] действия, и выражает собой инвариантность лагранжиана[3] по отношению к некоторой непрерывной группе преобразований.

Теорема установлена в работах учёных гёттингенской школы Д. Гильберта, Ф. Клейна и Э. Нётер. В наиболее распространенной формулировке была доказана Эмми Нётер в 1918 году.

Формулировка теоремы в классической механике звучит следующим образом:

Каждой однопараметрической группе диффеоморфизмов[4] g^s(q_i), сохраняющих функцию Лагранжа, соответствует первый интеграл системы, равный:

В терминах инфинитезимальных преобразований, пусть инфинитезимальное преобразование координат имеет вид:

и функция Лагранжа инвариантна относительно этих преобразований, то есть

Тогда у системы существует первый интеграл, равный:

Теорему можно обобщить на случай преобразований, затрагивающих также и время, если представить её движение как зависящее от некоторого параметра τ, причем в процессе движения t = τ. Тогда из преобразований:

следует первый интеграл:

В классической механике законы сохранения энергии, импульса и момента импульса выводятся из однородности/изотропности лагранжиана системы — лагранжиан (функция Лагранжа) не меняется со временем сам по себе и не изменяется переносом или поворотом системы в пространстве. По сути это означает то, что при рассмотрении некой замкнутой в лаборатории системы будут получены одни и те же результаты — вне зависимости от расположения лаборатории и времени проведения эксперимента. Другие симметрии лагранжиана системы, если они есть, соответствуют другим сохраняющимся в данной системе величинам (интегралам движения[5]); например, симметрия лагранжиана гравитационной и кулоновской задачи двух тел приводит к сохранению не только энергии, импульса и момента импульса, но и вектора Лапласа — Рунге — Ленца[6].

§2. Применение теоремы Нетер.

Для примера я покажу применение теоремы Нетер к универсальным преобразованиям симметрии с рассмотрения сдвига во времени.

Чтобы получить это преобразование надо, очевидно, считать 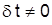за независимый и постоянный параметр преобразования, 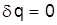. В силу этого полная производная функции Лагранжа по времени может быть записана следующим образом:

(если бы L зависела явно от времени, к правой стороне равенства добавился бы член ).

Заменяя производные согласно уравнениям Лагранжа на , получим:

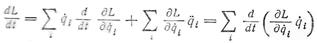
или

Отсюда видно, что величина

(1)

остается неизменной при движении замкнутой системы, то есть является одним из ее интегралов движения. Эта величина называется энергией системы. Аддитивность энергии непосредственно следует из аддитивности функции Лагранжа, через которую она выражается согласно (1) линейным образом.

Закон сохранения энергии справедлив не только для замкнутых систем, но и для систем, находящихся в постоянном (то есть не зависящем от времени) внешнем поле; единственное использованное в приведенном выводе свойство функции Лагранжа – отсутствие явной зависимости от времени – имеется и в ином случае. Механические системы, энергия которых сохраняется иногда называют консервативными.

Лагранжева функция замкнутой системы имеет вид:

где Т – квадратичная функция скоростей. Применяя к ней известную функцию Эйлера об однородных функциях, получим:

Подставляя это значение в (1), найдем:

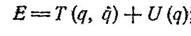
в декартовых координатах:

Таким образом, энергия системы может быть представлена в виде суммы двух существенно различных членов: кинетической энергии, зависящей от скоростей, и потенциальной энергии, зависящей только от координат частиц.

Заключение

«Послушайте - и Вы забудете, посмотрите - и Вы запомните, сделайте - и Вы поймете»

Конфуций

       Признаюсь, что тема реферата оказалась гораздо сложнее, чем я предполагала. Теорема Нётер, с помощью которой можно найти связь между свойствами пространства и времени и законами сохранения, содержала довольно много новых понятий, некоторые из которых мне было не очень просто понять. Однако, я постаралась разобраться с основной теорией, и в самом конце своего реферата представила применения данной теоремы для выведения закона сохранения энергии.

       Во время работы над рефератом я ответила на все вопросы поставленные мною во введении. Я рассмотрела четыре основных закона сохранения, изучила свойства пространства и времени и познакомилась с теоремой Э. Нётер. Также я решила проблему своего реферата, то есть показала, что в физике все взаимосвязано. Да и не только в физике, а в мире вцелом. Даже то, что в течении работы по физике я изучила огромное количество литературы по математике является тому подтверждением. Главное, что я достигла поставленное мною цели, нашла связь законов сохранения с пространством и временем.

       Проведенная мною работа оказалась для меня очень полезной. Я лучше изучила материал и теперь знаю выведение законов сохранения разными способами. Надеюсь, что данная работа поможет мне при дальнейшем изучении физики.

Список используемой литературы

1. Аженов Т.П. О причине времени // Вопр. философии. 1996. № 1.

2. Андреев Э.П. Пространство микромира, М., «Наука», 1969.

3. Ахундов М.Д. Концепции пространства и времени: истоки, эволюция, перспективы, М., «Наука», 1982.

4. Гельфер Я.М. Законы сохранения, М., «Наука», 1967. - 264 с.

5. Готт В.С. Удивительный неисчерпаемый познаваемый мир, М. «Знание», 1974. - 224 с.

6. Гельфер Я.М., Законы сохранения, М., «Наука», 1967.-263с.

7. Друянов Л.А. Законы природы и их познание, М. «Просвещение», 1982.- 112 с., ил.

8. Жирнов Н.И., Классическая механика, М., «Просвещение», 1980.-303с.

9. Ландау Л. Д., Лифшиц Е. М., Теоретическая физика. Механика , М., «Наука», 1988.

10. Райхенбах Г. Философия пространства и времени, М.: Наука, 1985.

11. Сиама Д. Физические принципы общей теории относительности, М.: Мир, 1971.

12. Семихатов А., Симметрия как зеркало мирового устройства, Наука и жизнь, 1996.-№8,9.

13. Спасский Б. И.. История физики. М., "Высшая школа", 1977.

14. Физический энциклопедический словарь / Гл.ред. А.М.Прохоров, М.: Сов.

15. Философский словарь / Под ред. И.Т.Фролова. - 4-е изд. - М.: Политиздат, 1981. - 445 с.

16. Философия естествознания, М.: Политиздат, 1966.

17. Шмутцер Э., Симметрии и законы сохранения в физике/Пер. с нем., М., «Мир», 1974-159с.

18. Энциклопедия, 1983. -928 с., ил., 2 л. цв. ил.

[1] Ама́лия Э́мми Нётер (нем. Amalie Emmy Noether ; 23 марта 1882, Эрланген, Германия — 14 апреля 1935, Брин-Мор, Пенсильвания, США) — выдающийся немецкий математик, «самая крупная женщина-математик, когда-либо существовавшая»

[2] Функциона́л традиционно — функция, определённая на множестве функций со значениями обычно в вещественных числах

[3] Лагранжиа́н, функция Лагранжа динамической системы, названа в честь Жозефа Луи Лагранжа, является функцией динамических переменных и описывает уравнения движения системы. Уравнения движения в этом подходе получаются из принципа наименьшего действия, записываемого как где действие — функционал обозначает множество параметров системы.

[4] Диффеоморфизм — взаимно однозначное и непрерывно дифференцируемое отображение гладкого многообразия M в гладкое многообразие N, обратное к которому тоже является непрерывно дифференцируемым.

[5] В механике любая функция называется интегралом движения, где q — обобщённые координаты, — обобщённые скорости системы.

[6] В классической механике ве́ктором Лапла́са — Ру́нге — Ле́нца называется вектор, в основном используемый для описания формы и ориентации орбиты, по которой одно небесное тело обращается вокруг другого (например, орбиты, по которой планета вращается вокруг звезды). В случае с двумя телами, взаимодействие которых описывается законом всемирного тяготения Ньютона, вектор Лапласа — Рунге — Ленца представляет собой интеграл движения, то есть его направление и величина являются постоянными независимо от того, в какой точке орбиты они вычисляются

2019-12-29

194

Обсуждений (0)

0.00 из 5.00 0 оценок

Обсуждение в статье: Глава III . Связь законов сохранения с пространством и временем.

Обсуждений еще не было, будьте первым... ↓↓↓