Пример 3.4-1. (Отсутствие допустимых решений)

 

Рассмотрим следующую задачу.

 

Максимизировать z = 3x1 + 2x2

 

при выполнении условий

 

2x1 + x2 <= 2,

  3x1 + 4x3 >= 12,

x1, x2 >= 0.

 

Результат применения симплекс-метода представлен в следующей таблице.

Итерация	Базис	x1	x2	x4	x3	R	Решение
Начальная	z	-3 -3M	-2 -4M	M	0	0	-12M
Вводится	x3	2	1	0	1	0	2
Исключается	R	3	4	-1	0	1	12
Первая	z	1 + 5M	0	M	2 + 4M	0	4 – 4M
(псевдооптимум)	x2	2	1	0	1	0	2
	R	-5	0	1	-4	1	4

 

Данные из этой таблицы показывают, что в точке оптимума искусственная переменная R имеет положительное значение (= 4), что свидетельствует об отсутствии допустимого решения. На рис. 3.4 графически представлена ситуация данной задачи. Алгоритмы симплекс-метода, допуская положительные значения искусственной переменной, по существу, превращает неравенство 3x1 + 4x3 >= 12 в 3x1 + 4x3 <= 12. (Объясните, почему так происходит.) В результате получаем то, что можно назвать псевдооптимальным решением.

 

Рис. 3.4

 

 

2. Практическая часть.

 

Постановка задачи.

 

Решить задачи:

 

1. F = 14x1 + 10x2 + 14x3 + 14x4 → max

 

при ограничениях:

 

4x1 + 2x2 + 2x3 + x4 <= 35;

x1 + x2 + 2x3 + 3x4 <= 30;

3x1 + x2 + 2x3 + x4 <= 40;

xj >= 0, j = 1, 2, 3, 4.

 

2. F = x1 + x2 → max

 

при ограничениях:

 

x1 – 4x2 – 4 <= 0;

3x1 – x2 >= 0;

x1 + x2 – 4 >= 0;

x1 >= 0, x2 >= 0.

 

 

Решение.

 

1.  F = 14x1 + 10x2 + 14x3 + 14x4 → max

при ограничениях:

4x1 + 2x2 + 2x3 + x4 <= 35;

x1 + x2 + 2x3 + 3x4 <= 30;

3x1 + x2 + 2x3 + x4 <= 40;

xj >= 0, j = 1, 2, 3, 4.

 

Переведём систему в канонический вид для решения симплексным методом.

4x1 + 2x2 + 2x3 + x4 + x5 = 35;

x1 + x2 + 2x3 + 3x4 + x6 = 30;

3x1 + x2 + 2x3 + x4 + x7 = 40;

xj >= 0, j = 1, 2, 3, 4, 5, 6, 7.

 

14x1 + 10x2 + 14x3 + 14x4 + 0x5 + 0x6 + 0x7 → max

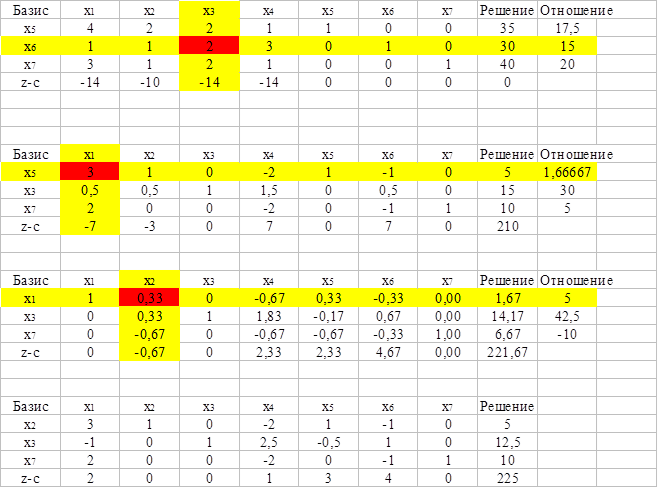
Ответ: max z = 225 при x2 = 5, x3 = 12,5, x7 = 10, x1 = x4 = x5 = x6 = 0.

 

Двухэтапный метод.

 

2.   F = x1 + x2 → max

 

при ограничениях:

x1 – 4x2 – 4 <= 0;

3x1 – x2 >= 0;

x1 + x2 – 4 >= 0;

x1, x2 >= 0.

 

Переведём в канонический вид и добавим искусственные переменные.

f = x1 + x2 + 0x3 + 0x4 + 0x5 – Mx0 – Mx7 → max.

x1 – 4x2 – 4 + x3 = 0;

3x1 – x2 – x4 + x6 = 0;

x1 + x2 – 4 – x5 + x7 = 0;

x1, x2, x3, x4, x5, x6, x7 >= 0;

 

Этап 1.

Z = x6 + x7 → min

Базис	x1	x2	x3	x4	x5	x6	x7	Решение
x3	1	-4	1	0	0	0	0	4
x6	3	-1	0	-1	0	1	0	0
x7	1	1	0	0	-1	0	1	4
z - c	0	0	0	0	0	-1	-1	0

Так как базисные переменные x6 и x7 имеют ненулевые коэффициенты в (z - c) – строке, эту строку следует преобразовать:

 

(z - c):  0 0 0 0 0 -1 -1 0

+

1 * x6: 3 -1 0 -1 0 1 0 0

+

1 * x7: 1 1 0 0 -1 0 1 4

= (z - c): 4 0 0 -1 -1 0 0 4

Базис	x1	x2	x3	x4	x5	x6	x7	Решение	Отношение
x3	1	-4	1	0	0	0	0	4	4
x6	3	-1	0	-1	0	1	0	0	0 ←
x7	1	1	0	0	-1	0	1	4	4
(z - c)’	4	0	0	-1	-1	0	0	4

               ↑

Базис	x1	x2	x3	x4	x5	x6	x7	Решение	Отношение
x3	0	-3 и 2/3	1	1/3	0	-1/3	0	4
x1	1	-1/3	0	-1/3	0	1/3	0	0
x2	0	1 и 1/3	0	1/3	1	-1/3	1	4	3 ←
(z - c)’	0	4/3	0	1/3	-1	-4/3	0	4

                             ↑

Базис	x1	x2	x3	x4	x5	x6	x7	Решение	Отношение
x3	0	0	1	5/4	11/4	-5/4	11/4	4
x1	1	0	0	-1/4	1/4	1/4	1/4	0
x2	0	1	0	1/4	3/4	-1/4	3/4	4
(z - c)’	0	0	0	0	-2	-5/3	-1	4

 

Так как достигнуто min (z - c)’ = 0, то получено допустимое базисное решение для второго этапа: x1 = 1, x2 = 3, x3 = 15. Искусственные переменные могут быть исключены.

 

Этап 2.

Перепишем исходную задачу с учётом полученного базисного решения:

f = x1 + x2 + 0x3 + 0x4 + 0x9 → max

 

x3 + 5/4 x4 + 11/4 x5 = 15;

x1 – 1/4 x4 + 1/4 x5 = 1;

x2 + 1/4 x4 + 3/4 x5 = 3;

x1, x2, x3, x4, x5 >= 0.

 

Базис	x1	x2	x3	x4	x5	Решение
x1	1	0	0	1/4	1/4	1
x2	0	1	0	1/4	3/4	3
x3	0	0	1	5/4	11/4	15
(f - c)	1	-1	0	0	0	0

Согласуем значения в строке (f - c) с остальной частью таблицы:

 

(f - c): -1 -1 0 0 0 0

+

1 * x1: 1 0 0 -1/4 1/4 1

+

1 * x2: 0 1 0 1/4 3/4 3

= (f-c)’: 0 0 0 0 1 4

 

Исходное решение является оптимальным.

 

Ответ: max (f) = 4 при x1 = 1, x2 = 3, x3 = 15, x4 = 0, x5 = 0.

Так как небазисные переменные равны нулю, задача имет множество альтернативных оптимальных решений, находящихся н отрезке AB (x1+ x2 = 4).

 

 

Заключение.

 

Симлекс-метод – это характерный пример итерационных вычислений. используемых при решении большинства оптимизационных задач.

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Из теоретических положений, лежащих в основе симплекс-метода, следует, что оптимальное решение задачи линейного программирования соответствует крайней точке пространства допустимых решений задачи. В свою очередь, крайние точки пространства допустимых решений полностью определяются базисными решениями задачи ЛП, представленной в стандартной форме. Для компьютерной реализации симплекс-метода разработан способ использования искусственных переменных, что позволяет найти начальное базисное решение задачи. В этой главе также рассмотрены теоретические и практические аспекты особых случаев реализации симплекс-метода: вырожденность, альтернативные оптимальные решения, неограниченность и отсутствие допустимых решений.

 

 

Литература.

 

1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.

2. Гасс С. Линейное программирование. – М.: Физматгиз, 1961.

3. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование: Теория, методы и приложения. – М.: Наука, 1969.

4. Таха, Хэмди, А. Введение в исследование операций. 6-е издание. : Пер. с англ. — М.: Издательский дом "Вильяме", 2001. — 912 с. : ил. — Парал. тит. англ.

5. Н.Ш. Кремер, Б А Путко, И.М. Тришин, М.Н. Фрид­ман; Под ред. проф. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для И87 вузов  —М: ЮНИТИ, 2002.— 407 с.