Задачи идеальной интерполяции

В общем случае формула интерполяции имеет вид:

, (13)

- оценка значения i-ой выборки, - восстановленный первичный сигнал,

.

Интерполяция возможна в том случае, если в сигнале имеются корреляционные связи. Может быть поставлена задача оптимального выбора вида функции , при которой ошибка интерполяции минимальна.

Рассмотрим задачу идеальной интерполяции сигнала при предположении, что , т.е. отсутствуют внешние шумы и ошибки системы.

Пусть непрерывный первичный сигнал описывается корреляционной

функцией 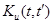. Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО

. (14)

Можно показать, что в этом случае оптимальная интерполирующая функция имеет вид:

, (15)

где - весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках , .

Т.о., оптимальная интерполирующая функция может быть определена как взвешенная сумма функций времени равных корреляционной функции первичного сигнала. Как следствие этой теории может бать доказана следующая теорема:

Если на интервале интерполяции  корреляционная функция и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 5).

Рисунок 5

Чем меньше , тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 6):

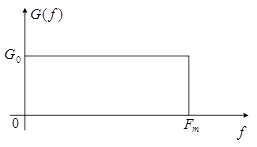
Рисунок 6

Известно, что в этом случае в соответствии с теоремой

В.А. Котельникова возможно разложение первичного сигнала в ряд:

, (16)

где - частота опроса. В точках  интерполирующая функция равна:

. (17)

Сопоставим этот результат с выражением для идеальной интерполирующей функции:

. (18)

Чтобы эти формулы совпали, необходимо чтобы при , а в случае , т. е. чтобы корреляционная функция имела вид:

. (19)

Такой функцией корреляции обладает сигнал с прямоугольным спектром, а условие  при  приводит к требованию, чтобы частота опроса .

Это соотношение не может быть использовано на практике по следующим причинам:

1. Сигнала с идеальным прямоугольным спектром не существует.

2. Число выборок .

На практике при представлении регулярными выборками частота опроса выбирается исходя из соотношения

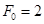ж , (20)

где определяется формой спектра сигнала, а ж – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.