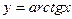|
Главная |
Задачи для самостоятельной работы
|
из
5.00
|
Применение дифференциала функции в приближенных вычислениях
Дифференциалом функции  в точке
в точке  называется главная, линейная относительно приращения аргумента
называется главная, линейная относительно приращения аргумента  часть приращения функции
часть приращения функции  , равная произведению производной функции в точке
, равная произведению производной функции в точке  на приращение независимой переменной:
на приращение независимой переменной:
 .
.
Отсюда приращение функции  отличается от ее дифференциала
отличается от ее дифференциала  на бесконечно малую величину и при достаточно малых значениях можно считать
на бесконечно малую величину и при достаточно малых значениях можно считать  или
или
 .
.
Приведенная формула используется в приближенных вычислениях, причем, чем меньше  , тем точнее формула.
, тем точнее формула.
Пример 3.1. Вычислить приближенно 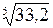
Решение. Рассмотрим функцию  . Это степенная функция и её производная
. Это степенная функция и её производная 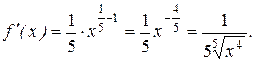
В качестве  требуется взять число, удовлетворяющее условиям:
требуется взять число, удовлетворяющее условиям:
- значение  известно или достаточно просто вычисляется;
известно или достаточно просто вычисляется;
- число  должно быть как можно более близким к числу 33,2.
должно быть как можно более близким к числу 33,2.
В нашем случае этим требованиям удовлетворяет число  = 32, для которого
= 32, для которого  = 2,
= 2,  = 33,2 -32 = 1,2.
= 33,2 -32 = 1,2.
Применяя формулу, находим искомое число:

 +
+  .
.
Пример 3.2. Найти время удвоения вклада в банк, если ставка банковского процента за год составляет 5% годовых.
Решение. За год вклад увеличивается в  раз, а за
раз, а за  лет вклад увеличится в
лет вклад увеличится в  раз. Теперь необходимо решить уравнение:
раз. Теперь необходимо решить уравнение:  =2. Логарифмируя, получаем
=2. Логарифмируя, получаем  , откуда
, откуда 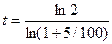 . Получим приближенную формулу для вычисления
. Получим приближенную формулу для вычисления  . Полагая
. Полагая  , найдем
, найдем  и в соответствии с приближенной формулой
и в соответствии с приближенной формулой  . В нашем случае
. В нашем случае  и
и  . Отсюда
. Отсюда  . Так как
. Так как  , находим время удвоения вклада
, находим время удвоения вклада 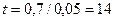 лет.
лет.
Вопросы для самопроверки
1. Дайте определение дифференциала функции в точке.
2. Почему формула, используемая для вычислений, является приближенной?
3. Каким условиям должно удовлетворять число  , входящее в приведенную формулу?
, входящее в приведенную формулу?
Задачи для самостоятельной работы
Вычислить приближённое значение  , заменив в точке
, заменив в точке  приращение функции
приращение функции  ее дифференциалом.
ее дифференциалом.
Таблица 3.1
| Номер варианта |

|

|

|
| 1 | 3 | 502 | 512 |
| 2 | 4 | 267 | 256 |
| 3 | 5 | 234 | 243 |
| 4 | 6 | 685 | 729 |
| 5 | 7 | 142 | 128 |
| 6 | 3 | 349 | 343 |
| 7 | 4 | 605 | 625 |
| 8 | 5 | 255 | 243 |
| 9 | 6 | 773 | 729 |
| 10 | 7 | 156 | 128 |
4. Исследование функций и построение их графиков
Если функция одной переменной задана в виде формулы  , то областью ее определения называют такое множество значений аргумента
, то областью ее определения называют такое множество значений аргумента  , на котором определены значения функции.
, на котором определены значения функции.
Пример 4.1. Значение функции  определены только для неотрицательных значений подкоренного выражения:
определены только для неотрицательных значений подкоренного выражения:  . Отсюда областью определения функции является полуинтервал [4;
. Отсюда областью определения функции является полуинтервал [4;  ).
).
Пример 4.2. Функция  не определена при таких значениях аргумента
не определена при таких значениях аргумента  , когда либо знаменатель равен нулю (
, когда либо знаменатель равен нулю (  ), либо подкоренное выражение отрицательно (
), либо подкоренное выражение отрицательно (  <3). Тогда областью определения служит множество, являющееся объединением интервалов (3;4)
<3). Тогда областью определения служит множество, являющееся объединением интервалов (3;4)  (4;5)
(4;5)  (5;
(5;  ).
).
Пример 4.3. Функция 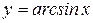 определена только на отрезке [-1;1], так как значение тригонометрической функции
определена только на отрезке [-1;1], так как значение тригонометрической функции  удовлетворяют неравенству: -1
удовлетворяют неравенству: -1 

 1.
1.
Функция  называется четной, если для любых значений
называется четной, если для любых значений  из области ее определения выполняется равенство
из области ее определения выполняется равенство
 ,
,
и нечетной, если справедливо другое соотношение:  . В других случаях функцию называют функцией общего вида.
. В других случаях функцию называют функцией общего вида.
Пример 4.4. Пусть  . Проверим:
. Проверим: 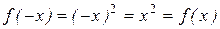 . Таким образом, эта функция является четной.
. Таким образом, эта функция является четной.
Для функции  верно
верно  . Отсюда эта функция является нечетной.
. Отсюда эта функция является нечетной.
Сумма предыдущих функций  является функцией общего вида, так как функция
является функцией общего вида, так как функция  не равна
не равна  и
и  .
.
Асимптотой графика функции  называется прямая, обладающая тем свойством, что расстояние от точки (
называется прямая, обладающая тем свойством, что расстояние от точки (  ;
;  ) плоскости до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Различают вертикальные (рис. 4.1), горизонтальные (рис. 4.2) и наклонные (рис. 4.3) асимптоты.
) плоскости до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Различают вертикальные (рис. 4.1), горизонтальные (рис. 4.2) и наклонные (рис. 4.3) асимптоты.


 |
|
| |||
| |||
 |
|
Вертикальные асимптоты функции следует искать либо в точках разрыва второго рода (хотя бы один из односторонних пределов функции в точке бесконечен или не существует), либо на концах ее области определения  , если
, если 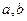 – конечные числа.
– конечные числа.
Если функция  определена на всей числовой оси и существует конечный предел
определена на всей числовой оси и существует конечный предел  , либо
, либо  , то прямая, задаваемая уравнением
, то прямая, задаваемая уравнением  , является правосторонней горизонтальной асимптотой, а прямая
, является правосторонней горизонтальной асимптотой, а прямая  - левосторонней горизонтальной асимптотой.
- левосторонней горизонтальной асимптотой.
Если существуют конечные пределы
 и
и  ,
,
то прямая  является наклонной асимптотой графика функции. Наклонная асимптота также может быть правосторонней (
является наклонной асимптотой графика функции. Наклонная асимптота также может быть правосторонней (  ) или левосторонней (
) или левосторонней (  ).
).
Функция  называется возрастающей на множестве
называется возрастающей на множестве  , если для любых
, если для любых  , таких, что
, таких, что  >
>  , выполняется неравенство:
, выполняется неравенство: 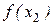 >
>  (убывающей, если при этом:
(убывающей, если при этом: 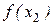 <
<  ). Множество
). Множество  в этом случае называют интервалом монотонности функции.
в этом случае называют интервалом монотонности функции.
Справедливо следующее достаточное условие монотонности функции: если производная дифференцируемой функции внутри множества  положительна (отрицательна), то функция возрастает (убывает) на этом множестве.
положительна (отрицательна), то функция возрастает (убывает) на этом множестве.
Пример 4.5. Дана функция  . Найти ее интервалы возрастания и убывания.
. Найти ее интервалы возрастания и убывания.
Решение. Найдем ее производную  . Очевидно, что
. Очевидно, что  >0 при
>0 при  >3 и
>3 и  <0 при
<0 при  <3. Отсюда функция убывает на интервале (
<3. Отсюда функция убывает на интервале (  ;3 ) и возрастает на (3;
;3 ) и возрастает на (3;  ).
).
Точка  называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если в некоторой окрестности точки
, если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство  (
(  ). Значение функции в точке
). Значение функции в точке  называется максимумом (минимумом). Максимум и минимум функции объединяются общим названием экстремум функции.
называется максимумом (минимумом). Максимум и минимум функции объединяются общим названием экстремум функции.
Для того чтобы функция  имела экстремум в точке
имела экстремум в точке  необходимо, чтобы ее производная в этой точке равнялась нулю (
необходимо, чтобы ее производная в этой точке равнялась нулю (  ) или не существовала.
) или не существовала.
Точки, в которых производная функции равна нулю, называются стационарными точками функции. В стационарной точке не обязательно должен быть экстремум функции. Для нахождения экстремумов требуется дополнительно исследовать стационарные точки функции, например, путем использования достаточных условий экстремума.
Первое из них заключается в том, что если при переходе через стационарную точку  слева направо производная дифференцируемой функции меняет знак с плюса на минус, то в точке достигается локальный максимум. Если знак изменяется с минуса на плюс, то это точка минимума функции.
слева направо производная дифференцируемой функции меняет знак с плюса на минус, то в точке достигается локальный максимум. Если знак изменяется с минуса на плюс, то это точка минимума функции.
Если же изменение знака производной при переходе через исследуемую точку не происходит, то в данной точке экстремума нет.
Второе достаточное условие экстремума функции в стационарной точке использует вторую производную функции: если  <0, то
<0, то  является точкой максимума, а если
является точкой максимума, а если  >0, то
>0, то  - точка минимума. При
- точка минимума. При  =0 вопрос о типе экстремума остается открытым.
=0 вопрос о типе экстремума остается открытым.
Функция  называется выпуклой (вогнутой) на множестве
называется выпуклой (вогнутой) на множестве  , если для любых двух значений
, если для любых двух значений  выполняется неравенство:
выполняется неравенство:



 .
.












Рис.4.4. График выпуклой функции
Если вторая производная дважды дифференцируемой функции  положительна (отрицательна) внутри множества
положительна (отрицательна) внутри множества  , то функция вогнута (выпукла) на множестве
, то функция вогнута (выпукла) на множестве  .
.
Точкой перегиба графика непрерывной функции  называется точка, разделяющие интервалы, в которых функция выпукла и вогнута.
называется точка, разделяющие интервалы, в которых функция выпукла и вогнута.
Вторая производная  дважды дифференцируемой функции в точке перегиба
дважды дифференцируемой функции в точке перегиба  равна нулю, то есть
равна нулю, то есть  = 0.
= 0.
Если вторая производная при переходе через некоторую точку  меняет свой знак, то
меняет свой знак, то  является точка перегиба ее графика.
является точка перегиба ее графика.
При исследовании функции и построении ее графика рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график достаточно исследовать только для положительных значений  , а для
, а для  <0 график симметричен относительно оси
<0 график симметричен относительно оси  в случае четности функции и симметричен относительно начала координат – для нечетной функции).
в случае четности функции и симметричен относительно начала координат – для нечетной функции).
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.
5. Найти интервалы возрастания и убывания функции и точки экстремума.
6. Найти интервалы выпуклости и вогнутости функции и точки перегиба.
7. Найти точки пересечения функции с осями координат.
Пример 4.6. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. 1.Функция представляет многочлен 3-й степени, поэтому она определена и непрерывна для всех 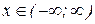 .
.
2. Найдем значение функции при значении аргумента (- 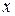 ):
):
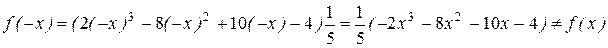 ,
,
а также  .
.
Таким образом, исследуемая функция является функцией общего вида и ее требуется исследовать на всей числовой оси.
3. Функция непрерывна на всей числовой оси, точек разрыва второго рода не имеет, следовательно, у нее вертикальные асимптоты отсутствуют.
4. Рассмотрим поведение функции в бесконечности.
Найдем пределы:
 ;
;

Так как пределы не являются конечными, то горизонтальных асимптот у функции нет.
Далее проверим наличие у функции наклонных асимптот. Вычислим предел:
 .
.
Поскольку предел не является конечными, то наклонные асимптоты также отсутствуют. Если бы предел являлся конечным и равнялся k, то требовалось найти другой предел
 .
.
В случае, когда он также конечен (равен числу b), устанавливается наличие наклонной асимптоты, задаваемой уравнением  .
.
Для определения интервалов монотонности функции найдем ее производную:
 .
.
Производная также определена и непрерывна на всей числовой оси. Отсюда критическими точками могут быть только те, в которых производная равна нулю.
Для нахождения стационарных точек функции приравниваем производную нулю:

и решаем квадратное уравнение:
 =
=  = 4,
= 4,
 ,
, 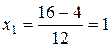
Теперь можно записать:  =0.
=0.
В итоге функция имеет две стационарные точки  .
.
Используя метод интервалов, найдем интервалы знакопостоянства производной функции.
 |
1 _ 5/3
Рис.4.5
При  <1 и
<1 и  >5/3 производная
>5/3 производная  >0, т.е. интервалы
>0, т.е. интервалы  и
и  являются интервалами возрастания функции.
являются интервалами возрастания функции.
При 1<  <5/3 имеем
<5/3 имеем  <0 и интервалом убывания является
<0 и интервалом убывания является  .
.
Поскольку при  <1 знак
<1 знак  >0, а при
>0, а при  >1
>1  <0, то стационарная точка
<0, то стационарная точка  = 1 является точкой максимума функции.
= 1 является точкой максимума функции.
В другой стационарной точке  =
=  имеем
имеем  <0 слева от нее и
<0 слева от нее и  >0 справа. Следовательно, в точке
>0 справа. Следовательно, в точке  =
=  функция имеет локальный минимум.
функция имеет локальный минимум.
5. Для нахождения интервалов выпуклости вычислим вторую производную функции
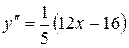 .
.
Вторая производная также определена на всей числовой оси и точки, где она не существует, отсутствуют.
Приравнивая вторую производную к нулю:
 = 0,
= 0,
находим точку  3 =
3 = 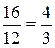 , которая может быть точкой перегиба.
, которая может быть точкой перегиба.
Если  <4/3, то
<4/3, то 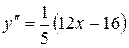 <0 и на интервале
<0 и на интервале  функция вогнута. При
функция вогнута. При  >4/3
>4/3  >0 и интервал
>0 и интервал  является интервалом выпуклости функции.
является интервалом выпуклости функции.
В итоге, поскольку при переходе точки 
 производная меняет знак, то
производная меняет знак, то 
 является точкой перегиба функции.
является точкой перегиба функции.
6. Определим точки пересечения функции с координатными осями. Полагая аргумент  =0, находим точку пересечения графика функции с осью ординат
=0, находим точку пересечения графика функции с осью ординат  :
:  .
.
Записывая уравнение  ,
,
найдем точки пересечения графика с осью абсцисс. Методом перебора из делителей свободного члена (равного 4) определяем, что  =2 является корнем этого уравнения. Разделим многочлен левой части уравнения на линейный бином (
=2 является корнем этого уравнения. Разделим многочлен левой части уравнения на линейный бином (  ):
):








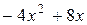




0 .
Отсюда уравнение можно записать в виде
 .
.
Решением квадратного уравнения  является
является  =1 (кратный корень, поэтому график функции касается в точке
=1 (кратный корень, поэтому график функции касается в точке  =1 координатной оси).
=1 координатной оси).
Для удобства построения графика функции полученные результаты запишем в следующую таблицу.
Таблица 4.1
| Интервал изменения или значение аргумента | Значения функции
| Знак или значение | Выводы | Фрагмент графика функции | ||||

| 
| |||||||
(-  ;1) ;1)
| + | - | Функция возрастает и выпукла | 
| ||||
 =1 =1
| 0 | 0 | - | Точка максимума |
| |||
(1;  ) )
| - | - | Убывает и выпукла | 
| ||||
 = = 
| - | 0 | Точка перегиба графика |  
| ||||
(  ; ;  ) )
| - | + | Убывает и вогнута |  
| ||||
 = = 
| - 
| 0 | + | Точка минимума | ||||
(  ; ;  ) )
| + | + | Возрастает и вогнута | 
| ||||
|

|

|

|
|

|
|
|
|


Рис. 4.6. График исследуемой функции
Вопросы для самопроверки
|
из
5.00
|
Обсуждение в статье: Задачи для самостоятельной работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы