 |
Главная |
Вычислите коэффициент корреляции
|
из
5.00
|
Коэффициент корреляции вычисляется по следующей формуле:
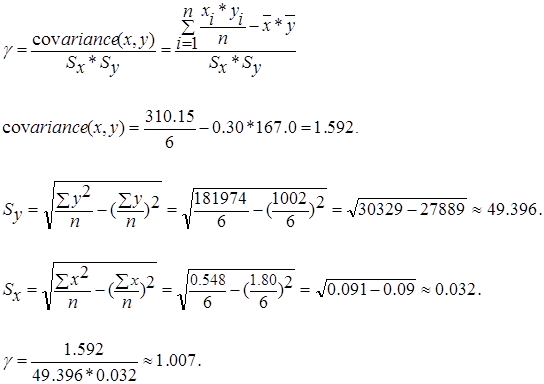
Для оценки значимости коэффициента корреляции на начальном этапе исследования можно пользоваться грубой оценкой:
При |γ| ≥ 0,70 имеется сильная линейная связь.
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. В частности, проверка качества отдельных видов продукции может быть связана с ее уничтожением (оценка крепости нити на разрыв, дегустация продуктов питания и т.п.); другие совокупности настолько велики, что было бы физически невозможно собрать данные в отношении каждого из их членов (например, при изучении пассажиропотоков или цен на рынках, исследованиях бюджетов семей). Выборочное наблюдение используют также для проверки результатов сплошного наблюдения.
Ту часть единиц, которые отобраны для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, – генеральной. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезен тативна (представительна).
Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо иной фактор, кроме случая.

Рис.1. Формы, виды и способы статистического наблюдения
Существуют различные способы формирования выборочной совокупности. Это, во-первых, индивидуальный отбор, включающий такие разновидности, как собственно случайный, механический, стратифицированный, и, во-вторых, серийный, или гнездовой, отбор.
Собственно случайный отбор, или случайная выборка, осуществляется с помощью жеребьевки либо по таблице случайных чисел. В первом случае всем элементам генеральной совокупности присваивается порядковый номер и на каждый элемент заводится жребий – пронумерованные шары или карточки-фишки, которые перемешиваются и помещаются в ящик, из которого затем отбираются наудачу. Во втором случае производится выбор случайных чисел (из специальных таблиц), которые образуют порядковые номера для отбора. Числа в таблицах обычно печатаются в виде блоков цифр (чтобы сделать таблицы более удобными для чтения по сравнению с не разбитой на блоки массой цифр), причем эти объединения в блоки не имеют статистического значения. Например, это могут быть числа:
5489, 5583, 3156, 0835,1988, 3912.
Применение комбинаций этих цифр зависит от размера совокупности: если в совокупности 1000 единиц, то порядковый номер каждой единицы должен состоять из трех цифр от 000 до 999. В таком случае приведенные выше случайные числа дали бы первые 8 номеров единиц выборочной совокупности:
548, 955, 833,156, 083, 519, 883, 912.
Дополнительные номера могут быть получены из последующих блоков тем же способом. Несколько сложнее выглядит процедура назначения номеров, отбираемых в выборочную совокупность, для случая произвольного объема генеральной. Теперь из случайных чисел таблиц формируется последовательность случайных величин, равномерно распределенных в интервале от 0 до 1. Могут использоваться и так называемые псевдослучайные числа, т.е. полученные по определенному алгоритму вручную или с помощью ПЭВМ. В нашем примере такими числами можно было бы считать:
0,5489, 0,5583, 0,3156, 0,0835; 0,1988, 0,3912 и т.д.
Предположим, что генеральная совокупность состоит из 7328 единиц. Тогда в выборочную совокупность должны войти единицы с номерами:
7328 х 0,5489 = 4022,3 или 4022;
7328 х 0,5583 = 4091,2 или 4091;
7328 х 0,3156 = 2312,7 или 2313;
7328x0,0835 = 611,9 или 612;
7328 х 0,1988 = 1456,8 или 1457;
7328 х 0,3912 = 2866,7 или 2867.
Процесс формирования случайных чисел и определения номера отбираемой единицы продолжается до тех пор, пока не будет получен заданный объем выборочной совокупности.
До настоящего времени на практике в качестве способа отбора обычно применяют механическое формирование выборочной совокупности, не связанное с процедурами получения случайных чисел. При этом способе отбирается каждый (n/N)-й элемент генеральной совокупности. Например, если имеется совокупность из 100 тыс. ед. и требуется выборка в 1000, то в нее попадет каждый сотый элемент. Если единицы в совокупности не ранжированы относительно изучаемого признака, то первый элемент выбирается наугад, произвольно, а если ранжированы, то из середины первой сотни. При достаточно большой совокупности этот способ отбора близок к собственно случайному, при условии, что применяемый список не составлен таким образом, чтобы какие-то единицы совокупности имели больше шансов попасть в выборку. К сожалению, это условие может нарушается. Так, использование 25%-й механической выборки при обследовании городского населения может привести к тому, что для каждого этажа при 4-квартирных площадках будет выбран один и тот же тип квартир (например, только трехкомнатные).
Отбор единиц из неоднородной совокупности осуществляется так называемым стратифицированным (расслоенным) способом, дающим модифицированную форму выборки. В этом случае генеральную совокупность предварительно разбивают на однородные группы с помощью типологической группировки, после чего производят отбор единиц из каждой группы в выборочную совокупность случайным или механическим способом. Этот метод гарантирует, что единицы разных групп (слоев) включаются в выборку пропорционально их численности в генеральной совокупности.
Особая форма составления выборки предполагает серийный, или гнездовой, отбор, при котором в порядке случайной или механической выборки выбирают не единицы, а определенные районы, серии (гнезда), внутри которых производится сплошное наблюдение.
Особенности обследуемых объектов определяют два метода отбора единиц в выборочную совокупность – повторный (отбор по схеме возвращенного шара) и бесповторный (отбор по схеме невозвращенного шара) При повторном отборе каждая попавшая в выборку единица или серия возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность всех единиц генеральной совокупности остается одинаковой. Бесповторный отбор означает, что каждая отобранная единица (или серия) не возвращается в генеральную совокупность и не может подвергнуться вторичной регистрации, а потому для остальных единиц вероятность попасть в выборку увеличивается.
Бесповторный отбор дает более точные результаты по сравнению с повторным, так как при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности. Поэтому он находит более широкое применение в статистической практике. И только в тех случаях, когда бесповторный отбор провести нельзя, используется повторная выборка (при обследовании потребительского спроса, пассажирооборота и т.п.).
В вопросе № 3 дается пример случайной выборки.
Вопрос № 3
Z-Тест
Условие задачи:
Булочная Truro отчиталась, что количество продаваемого ежедневно хлеба составляет 3000. Работник желает проверить точность данного отчета. Случайная выборка за 36 дней показала, что в среднем ежедневные продажи составляют 3150 с колебаниями в 300. Проверьте с 1% уровнем значимости, можно ли принять отчет булочной.
Решение:
1. Сформулируем нулевую и альтернативные гипотезы:
Н0 = {количество ежедневно продаваемого хлеба составляет}:μ = 3000.
Н1 = {количество ежедневно продаваемого хлеба не равно}:μ ≠ 3000.
2. Уровень значимости α = 0,01 (это вероятность отклонения верной гипотезы)
По таблице распределения Стьюдента при заданном уровне значимости α и числу степеней свободы df, где df = n – 1 (n – объем выборки) находим квантили (критические точки)
 распределения Стьюдента. Они равны:
распределения Стьюдента. Они равны:

Accept H0 if -2.75 < Z < 2.75.
Reject H0 if Z ≤ -2.75; Z ≥ 2.75.
3. 
4.  что свидетельствует о попадании в критическую область, то есть
что свидетельствует о попадании в критическую область, то есть  выпадает из зоны значений принятия гипотезы Н0.
выпадает из зоны значений принятия гипотезы Н0.
5. Следовательно, гипотеза Н0 отвергается, то есть при 1% уровне значимости количество продаваемого ежедневно хлеба в количестве 3000 в виде отчета принята быть не может.
В качестве примеров распределений непрерывной случайной величины приведем следующие часто используемые в задачах управления качеством распределения, которые понадобятся нам для дальнейшей работы.
Нормальное (гауссовское) распределение имеет вид
 ,
, 
Здесь  – среднее,
– среднее,  – дисперсия распределения СВ.
– дисперсия распределения СВ.
Равномерное (равновероятное для дискретных СВ) распределение на интервале [a,b] описывается соотношением

Среднее значение и дисперсия этого распределения равны соответственно
 ,
,  .
.
Распределение 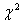 (хи – квадрат). Если
(хи – квадрат). Если  ,
,  - независимые нормально распределенные числа с нулевым средним и единичной дисперсией, то статистика (функция случайных величин)
- независимые нормально распределенные числа с нулевым средним и единичной дисперсией, то статистика (функция случайных величин)
 подчиняется распределению
подчиняется распределению 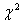 с k степенями свободы.
с k степенями свободы.
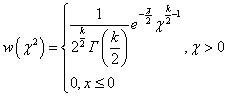
Здесь  - гамма функция. Математическое ожидание и дисперсия данного распределения имеют вид соответственно
- гамма функция. Математическое ожидание и дисперсия данного распределения имеют вид соответственно

 .
.
Распределение Стьюдента (t - распределение).
Пусть z – нормальная случайная величина с нулевым математическим ожиданием и единичной дисперсией. Пусть также v – независимая от z СВ, имеющая 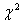 распределение с k степенями свободы. Тогда СВ
распределение с k степенями свободы. Тогда СВ

имеет t - распределение с k степенями свободы

Среднее значение и дисперсия равны соответственно
 .
.
Распределение Фишера-Снедекора.
Если u и v независимые СВ, распределенные по закону 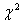 со степенями свободы
со степенями свободы  и
и  соответственно, то СВ
соответственно, то СВ

имеет распределение Фишера-Снедекора

Здесь  ., среднее значение и дисперсия равны соответственно
., среднее значение и дисперсия равны соответственно
 ,
,  .
.
Приведем примеры распределений дискретной СВ, используемые в задачах управления качеством.
Гипергеометрическое распределение, часто применяемое в задачах выборочного контроля, имеет вид

Здесь V - объем контролируемой партии, N – число изделий в выборке, k – число дефектных изделий в выборке, D – число дефектных изделий в партии,
 - число сочетаний из D по k.
- число сочетаний из D по k.
Среднее значение и дисперсия этого распределения равны соответственно
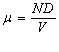 ,
,  .
.
В случае N<<V гипергеометрическое распределение хорошо аппроксимируется биномиальным распределением, вычисляемым по формуле

Здесь  - вероятность дефекта, остальные обозначения соответствуют приведенным для гипергеометрического распределения.
- вероятность дефекта, остальные обозначения соответствуют приведенным для гипергеометрического распределения.
Среднее значение и дисперсия для биномиального распределения вычисляются соответственно по формулам
 ,
,  .
.
В случае, если число испытаний N возрастает, а вероятность q уменьшается так, что Nq = const, биномиальное распределение стремится к распределению Пуассона
 .
.
Здесь N – объем испытуемой выборки, k – число интересующих исследователя событий, происшедших в процессе испытаний,  - среднее число событий в выборке (интенсивность потока событий). Среднее значение и дисперсия распределения Пуассона имеют вид
- среднее число событий в выборке (интенсивность потока событий). Среднее значение и дисперсия распределения Пуассона имеют вид 
Вопросу распределения вероятности касаются вопросы № 4 и № 5.
Вопрос № 4
Chi-Squared Distribution
Условие задачи
Менеджер розничного магазина хочет установить, соотносится или нет количество покупателей, приходящих ежедневно в магазин со временем суток. Счетчик дает следующую информацию, касающуюся количества продаж в разное время дня.
| Период времени | Количество продаж |
| 8.00 – 10.00 | 75 |
| 10.00 – 12.00 | 87 |
| 12.00 – 14.00 | 41 |
| 14.00 – 16.00 | 32 |
| 16.00 – 18.00 | 95 |
Если менеджер хочет проверить гипотезу, что продажи не соотносятся со временем суток на 5% уровне значимости, к какому выводу можно прийти.
Решение:
Сформулируем нулевую гипотезу:

Пусть случайная величина Х – момент продажи. Тогда следующая формулировка нулевой гипотезы является эквивалентной:
Н0 = {случайная величина Х имеет равномерное распределение на [800; 1800]}; согласно равномерному закону, вероятность того, что случайная величина принадлежит одному из периодов равна:
 i = 1, …, 5,
i = 1, …, 5,
где Δi – длительность i-периода.

Расчетное значение статистики  получаем по формуле:
получаем по формуле:

Табличное значение критерия при уровне значимости α = 0,05 и числе степеней свободы (k – 1) = (5-1) = 4 равно:

Так как  что гипотеза Н0 отвергается .
что гипотеза Н0 отвергается .
Значит количество продаж в разные периоды времени за сутки действительно различное.
Вопрос № 5
Распределение вероятности
Условие задачи:
Существует 80% шанс, что обучаемый по программе в компании завершит программу успешно. Какова вероятность, что в группе из 4 выбранных случайным образом обучаемых:
5.1. Все четверо успешно завершат программу?
5.2. Максимум один обучающийся не справится с программой?
Решение:
В данной задаче имеем дело с числом Х появления события при 4 независимых опытах (обучаемые друг от друга независимы). Следовательно, дискретная случайная величина Х распределена по биномиальному закону, а ее возможные значения 0, 1, 2, 3, 4 соответствуют вероятностям:

Где 0 < Р < 1; q = 1 – p, m = 1, …, n.
Данное распределение зависит от двух параметров: р и n (т.е. от р = 80%/100% = 4/5; n = 4).
Составим ряд распределения:
| Х: | 0 | 1 | 2 | 3 | 4 |
| 1/625 | 16/625 | 192/625 | 256/625 | 256/625 |
Вероятность того, что никто не завершит успешно программу равна:

Вероятность того, что один человек завершит успешно программу равна:

Вероятность того, что два человека завершат успешно программу равна:

Вероятность того, что три человека завершат успешно программу равна:

5.1. Вероятность того, что все четверо завершат успешно программу равна:

5.2. Вероятность того, что максимум один обучающийся не справится с программой, определяется следующим образом.
Для ответа на данный вопрос необходимо составить ряд распределения случайной величины Х – числа появлений противоположного события в 4 опытах.
| Х: | 0 | 1 | … | m | … | n |
| Рn | 
| … | 
| … | qn |
При Х = 0: 
При Х = 1: 

При Х = 2: 

При Х = 3: 

При Х = 4: 

| Х: | 0 | 1 | 2 | 3 | 4 |
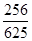
| 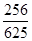
| 
| 
| 
|
Вероятность того, что максимум один обучающийся не справится с программой равна  при этом математическое ожидание не справившихся с программой равно:
при этом математическое ожидание не справившихся с программой равно:
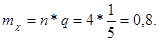
Список литературы
1. Добрынин А.И., Салов А.И. Экономика. - М.: Юрайт, 2002.
2. Попов А.И. Экономическая теория. СПб.; М.; Харьков; Минск: Питер, 2000.
3. Фишер С., Дорнбут Р., Шмалензи Р. Экономика. - М.: Дело, 1993.
4. Экономическая теория. / Под ред. Видяпина В.И. и др. – М.: ИНФРА-М, 2000.
5. Экономическая теория. / Под ред. Камаева В.Д. – М.: ВЛАДОС, 1999.
|
из
5.00
|
Обсуждение в статье: Вычислите коэффициент корреляции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

