 |
Главная |
Крутящие моменты, передаваемые валами, определяется по формуле
|
из
5.00
|
Ti=9550  .
.
T1=  H×м
H×м
T2 = 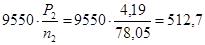 Н∙м
Н∙м
2. Расчет зубчатой передачи
2.1 Выбор материалов и способов термообработки шестерни и колеса. Расчет допускаемых напряжений.
Выбираем для шестерни и колеса сталь 45 с термообработкой улучшения для шестерни, с нормализацией – для колеса
НВ1=210 НВ2=190 [1, c.34, т. 3.3]
2.1.1 Расчет допускаемых контактных напряжения
[σн]= 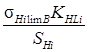
где i=1 для шестерни, i=2 для колеса;
sHilimB - предел контактной выносливости при симметричном цикле нагружения; Мпа
sHilimB = 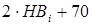
sH1limB =  МПа
МПа
sH2limB=  МПа
МПа
[ S H j ] - коэффициент безопасности, определяется способом термообработки; [1, с.33]
[S H ]= 1.1..1.2 S H= 1.15
KHLj - коэффициент долговечности;
KHLj = 
 1,
1,
где NH0j – базовое число циклов, определяемое твердостью боков поверхности зубьев;
NH0j= 
NH 01= 
NH 02 = 
NHEj – эквивалентное число циклов, определяемое сроком службы передачи, числом оборотов вала шестерни и валов колеса, коэффициентом использования;
NHEj = T∑ ∙k∙ni∙60,
где T∑ – срок службы зубчатой передачи; T∑=20000 часов
k - коэффициент использования передачи; k=0,8;
ni – частота вращения валов редуктора, n1= 277,07 об/мин, n2= 78,05 об/мин;
NHE1 = 20000∙0,8∙277,07∙60=2,6 ∙108
NHE2 = 20000∙0,8∙78,05∙60=0,7 ∙108
Поскольку 

Допускаемые контактные напряжения для шестерни и колеса
[sH1]=  МПа
МПа
[sH 2]= 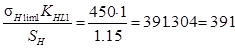 МПа
МПа
Для косозубой передачи принимается наименьшее из значений, полученных по зависимости
1. [σн]=0,45∙([σн1]+[σн2])= 0,45 (426+391)= 367 Мпа
2. [σн]=1,23∙ [σнi]min= 1,23∙391=481 Мпа
[σн]=367 Мпа
2.1.2. Расчет допускаемых напряжений изгиба
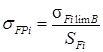 ,
,
где  - предел изгибной выносливости при отнулевом цикле нагружения; МПа
- предел изгибной выносливости при отнулевом цикле нагружения; МПа
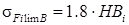 [1, c. 44, т.3.9]
[1, c. 44, т.3.9]
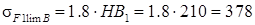 МПа
МПа
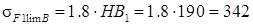 МПа
МПа
[SF] - коэффициент безопасности
[SF]= [SF]΄∙ [SF]΄΄,
где [SF]΄ - коэффициент, учитывающий механические свойства и твердость зубьев;
[SF]΄΄- коэффициент, учитывающий способ получения заготовки для шестерни или для колеса
[SF]΄=1,75 [1, с.44, т.3.9]
[SF]΄΄=1 [1, с.44]
[SF]=1,75
Допускаемые напряжения изгиба:
 МПа
МПа
 МПа
МПа
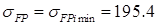 МПа
МПа
2.2 Расчет параметров зубчатой передачи
2.2.1 Расчет межосевого расстояния
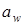 =
=  (u+1)
(u+1)  ,
,
где  - коэффициент, учитывающий тип передачи;
- коэффициент, учитывающий тип передачи;  = 43
= 43
 - коэффициент, учитывающий распределение нагрузки по длине зуба,
- коэффициент, учитывающий распределение нагрузки по длине зуба,  [1, c.32, т. 3.1]
[1, c.32, т. 3.1]
 - коэффициент ширины;
- коэффициент ширины;  = 0,25…0,5=0,4
= 0,25…0,5=0,4
u – стандартное передаточное отношение, u=u2=3,55;
T2 – крутящий момент на валу колеса, Т2 = 512,7 Н×м
αw =43∙(3,55+1) 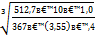 =178 мм
=178 мм
Округлим 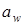 до ближайшего большего стандартного значения [1, с. 36] мм.
до ближайшего большего стандартного значения [1, с. 36] мм.
αw=180 мм
2.2.2 Расчет ширины колеса (расчетной ширины зубчатой передачи)
bw2=bw=ψba∙ αw=0,4∙180=72 мм
bw= 71 мм [1, с. 36]
2.2.3 Расчет модуля зацепления
m=(0,01…0,02) αw=1,8…3,6 мм
Округлим m до стандартного значения [1, с. 36]: m= 3 мм
2.2.4 Расчет суммарного числа зубьев шестерни и колеса, угла наклона зуба  в косозубой передаче
в косозубой передаче
Z∑=  ,
,
где β – угол наклона зуба
β= 8…15°=10°
Z∑=  =118,08
=118,08
Z  =118
=118
β = arcos  =arcos
=arcos  =arcos(0,9833)=10,4858=10°29`8``
=arcos(0,9833)=10,4858=10°29`8``
Z1=  25,9
25,9
Z1=26
Z2= Z  -Z1=118-26=92
-Z1=118-26=92
2.2.5 Расчет фактического передаточного отношения
иф=  3,538
3,538

[∆и]=±3,3%
∆и=  ∙100=0,33% < 3,3%
∙100=0,33% < 3,3%
2.3 Проверочный расчет зубчатой передачи
2.3.1 Расчет по контактным напряжениям
Контактные напряжения равны
 ,
,
где с – коэффициент, учитывающий тип передачи; с= 270
aw - межосевое расстояние; мм
bw - расчетная ширина зубчатой передачи; мм
T2 - крутящий момент на валу колеса; н∙мм
uф - фактическое передаточное отношение;
K Н - коэффициент нагрузки,
KН = KHα KHβ KНV.
v=ω1∙r1,
где ω1- угловая скорость шестерни, рад/м
ω1= 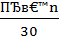
r1- радиус делительной окружности шестерни; мм
r1= 
v= 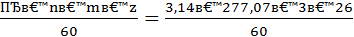 =1130,9 мм/с=1,13 м/с
=1130,9 мм/с=1,13 м/с
степень точности - 8
KHα – коэффициент, учитывающий распределение нагрузки между зубьями, KHα=1,09 [1, с. 39, т. 3.4]
KHβ - коэффициент, учитывающий распределение нагрузки по длине зуба,
KHβ =1,0 [1, с. 39, т. 3.5]
K Н V - динамический коэффициент, определяемый степенью точности изготовления передачи,
K Н V =1,0 [1, с. 40, т. 3.6]
KH=1,09×1,0×1,0=1,09
σн=  363,61 Мпа
363,61 Мпа
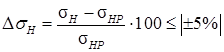
∆σн=  ∙100=0,92% <|±5%|
∙100=0,92% <|±5%|
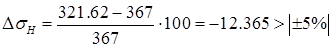
2.3.2 Расчет по напряжению изгиба

KF - коэффициент нагрузки;
YF - коэффициент формы зуба;
Yb - коэффициент, учитывающий влияние осевой силы в косозубой передаче на напряжение изгиба в основании зуба;
 - коэффициент, учитывающий распределения нагрузки между зубьями;
- коэффициент, учитывающий распределения нагрузки между зубьями;
m – модуль зацепления; мм
bw –ширина колеса; мм
 - окружное усилие, Н
- окружное усилие, Н
Ft = Ft1=Ft2= 
где T2 - крутящий момент на валу колеса;
 - диаметр начальной окружности колеса, мм
- диаметр начальной окружности колеса, мм

где  - диаметр начальной окружности шестерни, мм
- диаметр начальной окружности шестерни, мм
dw1=  =79,33 мм
=79,33 мм
dw2=79,33∙3,538=280,67 мм
Ft=  3653,4 н
3653,4 н
KF = KFβ ×KFV,
где KFβ - коэффициент, учитывающий распределение нагрузки по длине зуба;
KFV - динамический коэффициент,
KFV =1,1[1, c. 43, т.3.8]
Ψbd=  - коэффициент диаметра
- коэффициент диаметра
Ψbd= 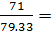 0,89
0,89
KFβ = 1,1 [1, c. 43, т.3.7]

KF = 1,1 ×1,1=1,21
YF =3,8[1, c. 42]
Yb=1-  0,926
0,926
KFα [1, c. 46]
Еβ=  1,39 > 1
1,39 > 1
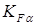 =0,92
=0,92
σw=  67,2 МПа>[GF]=195 Мпа
67,2 МПа>[GF]=195 Мпа
Условия изгибной прочности передачи выполняются
3. Первый этап эскизной компоновки редуктора
3.1 Компоновка зубчатой передачи в корпусе редуктора

|
|
dw1=79,33 мм
dw2=280,67 мм
bw1= bw2+3…5=75 мм
bw2=71 мм
 мм
мм
3.2 Компоновка валов
|
из
5.00
|
Обсуждение в статье: Крутящие моменты, передаваемые валами, определяется по формуле |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


